Régression à travers l’origine : définition & Exemple

La régression linéaire simple est une méthode qui peut être utilisée pour quantifier la relation entre une ou plusieurs variables prédictives et une variable de réponse .

Un modèle de régression linéaire simple prend la forme suivante :

y = β ₀ + β ₁ x

où:

• y : La valeur de la variable de réponse
• β ₀ : La valeur de la variable de réponse lorsque x = 0 (appelé terme « intercept »)
• β ₁ : L’augmentation moyenne de la variable de réponse associée à une augmentation d’une unité de x
• x : La valeur de la variable prédictive

Une version modifiée de ce modèle est connue sous le nom de régression par l’origine , qui force y à être égal à 0 lorsque x est égal à 0.

Ce type de modèle prend la forme suivante :

y = _β1x

Notez que le terme d’interception a été complètement supprimé du modèle.

Ce modèle est parfois utilisé lorsque les chercheurs savent que la variable de réponse doit être égale à zéro lorsque la variable prédictive est égale à zéro.

Dans le monde réel, ce type de modèle est le plus souvent utilisé dans les études forestières ou écologiques .

Par exemple, les chercheurs peuvent utiliser la circonférence des arbres pour prédire la hauteur des arbres. Si un arbre donné a une circonférence nulle, il doit avoir une hauteur nulle.

Ainsi, lors de l’ajustement d’un modèle de régression à ces données, il ne serait pas logique que le terme d’origine soit différent de zéro.

L’exemple suivant montre la différence entre l’ajustement d’un modèle de régression linéaire simple ordinaire et un modèle qui implémente la régression via l’origine.

Exemple : régression à travers l’origine

Supposons qu’un biologiste souhaite ajuster un modèle de régression utilisant la circonférence des arbres pour prédire la hauteur des arbres. Elle sort et collecte les mesures suivantes pour un échantillon de 15 arbres :

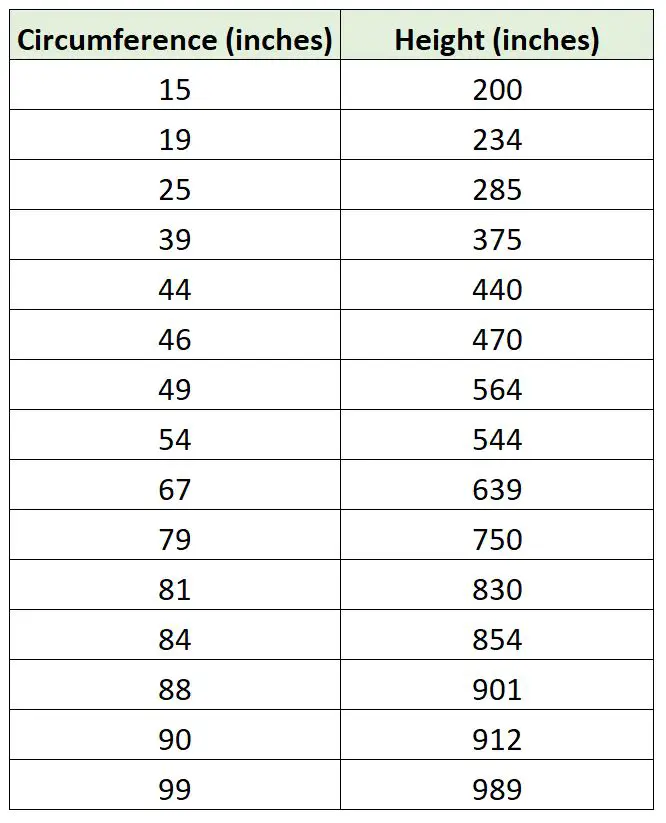
Nous pouvons utiliser le code suivant dans R pour ajuster un modèle de régression linéaire simple avec un modèle de régression qui n’utilise aucune interception et tracer les deux droites de régression :

#create data frame
df <- data.frame(circ=c(15, 19, 25, 39, 44, 46, 49, 54, 67, 79, 81, 84, 88, 90, 99),
                 height=c(200, 234, 285, 375, 440, 470, 564, 544, 639, 750, 830, 854,
                          901, 912, 989))

#fit a simple linear regression model
model <- lm(height ~ circ, data = df)

#fit regression through the origin
model_origin <- lm(height ~ 0 + ., data = df)

#create scatterplot
plot(df$circ, df$height, xlab='Circumference', ylab='Height',
     cex=1.5, pch=16, ylim=c(0,1000), xlim=c(0,100))

#add the fitted regression lines to the scatterplot
abline(model, col='blue', lwd=2)
abline(model_origin, lty='dashed', col='red', lwd=2)

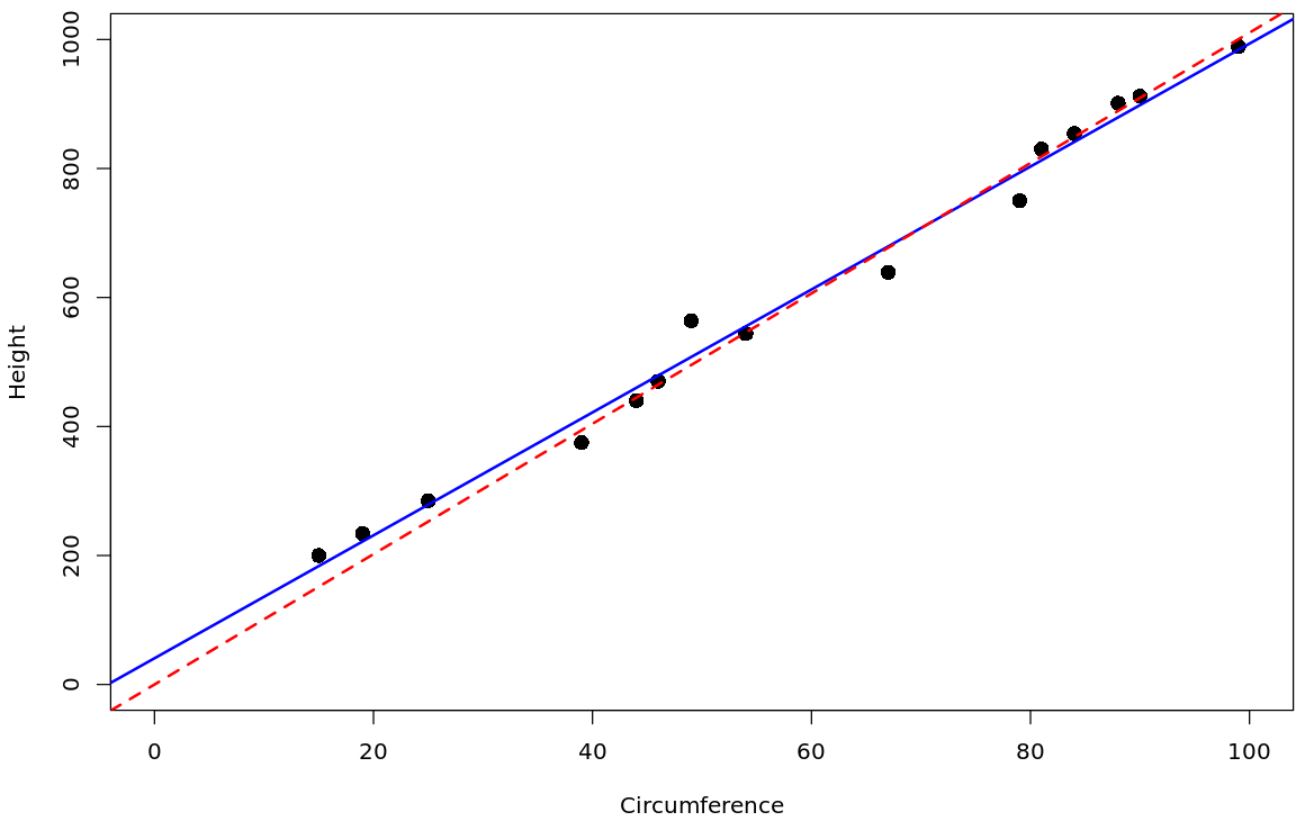
La ligne pointillée rouge représente le modèle de régression qui passe par l’origine et la ligne continue bleue représente le modèle de régression linéaire simple ordinaire.

Nous pouvons utiliser le code suivant dans R pour obtenir les estimations de coefficient pour chaque modèle :

#display coefficients for simple linear regression model
coef(model)

(Intercept)        circ 
  40.696971    9.529631 

#display coefficients for regression model through the origin
coef(model_origin)

    circ 
10.10574 

L’équation ajustée pour le modèle de régression linéaire simple est :

Hauteur = 40,6969 + 9,5296 (circonférence)

Et l’équation ajustée pour le modèle de régression via l’origine est :

Hauteur = 10,1057 (circonférence)

Notez que les estimations du coefficient pour la variable circonférence sont légèrement différentes.

Précautions concernant l’utilisation de la régression via l’origine

Avant d’utiliser la régression via l’origine, vous devez être absolument sûr qu’une valeur de 0 pour la variable prédictive implique une valeur de 0 pour la variable de réponse. Dans de nombreux scénarios, il est presque impossible de le savoir avec certitude.

Et si vous utilisez la régression via l’origine pour économiser un degré de liberté dans l’estimation de l’origine, cela fait rarement une différence substantielle si la taille de votre échantillon est suffisamment grande.

Si vous choisissez d’utiliser la régression via l’origine, assurez-vous d’exposer votre raisonnement dans votre analyse ou rapport final.

Ressources additionnelles

Les didacticiels suivants fournissent des informations supplémentaires sur la régression linéaire :

Introduction à la régression linéaire simple
Introduction à la régression linéaire multiple
Comment lire et interpréter un tableau de régression