Comment effectuer une régression pas à pas dans SAS (avec exemple)

La régression pas à pas est une procédure que nous pouvons utiliser pour construire un modèle de régression à partir d’un ensemble de variables prédictives en entrant et en supprimant des prédicteurs de manière étape par étape dans le modèle jusqu’à ce qu’il n’y ait plus de raison statistiquement valable d’en saisir ou d’en supprimer davantage.

L’objectif de la régression pas à pas est de créer un modèle de régression qui inclut toutes les variables prédictives qui sont statistiquement significativement liées à la variable de réponse .

Pour effectuer une régression pas à pas dans SAS, vous pouvez utiliser PROC REG avec l’instruction SELECTION .

L’exemple suivant montre comment effectuer une régression pas à pas dans SAS dans la pratique.

Exemple : effectuer une régression pas à pas dans SAS

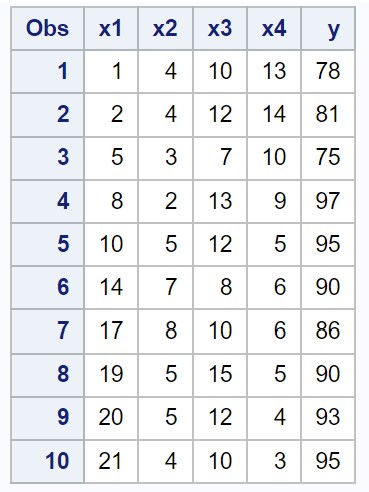
Supposons que nous ayons l’ensemble de données suivant dans SAS qui contient quatre variables prédictives (x1, x2, x3, x4) et une variable de réponse (y) :

/*create dataset*/
data my_data;
    input x1 x2 x3 x4 y;
    datalines;
1 4 10 13 78
2 4 12 14 81
5 3 7 10 75
8 2 13 9 97
10 5 12 5 95
14 7 8 6 90
17 8 10 6 86 
19 5 15 5 90
20 5 12 4 93
21 4 10 3 95
;
run;

/*view dataset*/
proc print data=my_data;

Supposons maintenant que nous souhaitions déterminer quelle combinaison de variables prédictives produira le meilleur modèle de régression linéaire multiple .

Lorsque nous parlons du « meilleur » modèle de régression, nous entendons le modèle qui maximise ou minimise certaines mesures.

Il existe deux mesures que nous utilisons couramment pour évaluer quel modèle de régression est le meilleur parmi un groupe de modèles potentiels :

1. R-carré ajusté : La valeur R-carré ajustée nous indique l’utilité d’un modèle, ajustée en fonction du nombre de prédicteurs dans un modèle. Le modèle avec la valeur R-carré ajustée la plus élevée est considéré comme le meilleur.

2. AIC : Le critère d’information d’Akaike (AIC) est une métrique utilisée pour comparer l’ajustement de différents modèles de régression. Le modèle avec la valeur AIC la plus basse est considéré comme le meilleur.

Heureusement, nous pouvons calculer à la fois les valeurs ajustées du R au carré et de l’AIC pour les modèles de régression dans SAS en utilisant PROC REG avec l’instruction SELECTION .

Le code suivant montre comment procéder :

/*perform stepwise multiple linear regression*/
proc reg data=my_data outest=est;
    model y=x1 x2 x3 x4 / selection=adjrsq aic ;
    output out=out p=p r=r;
run;
quit; 

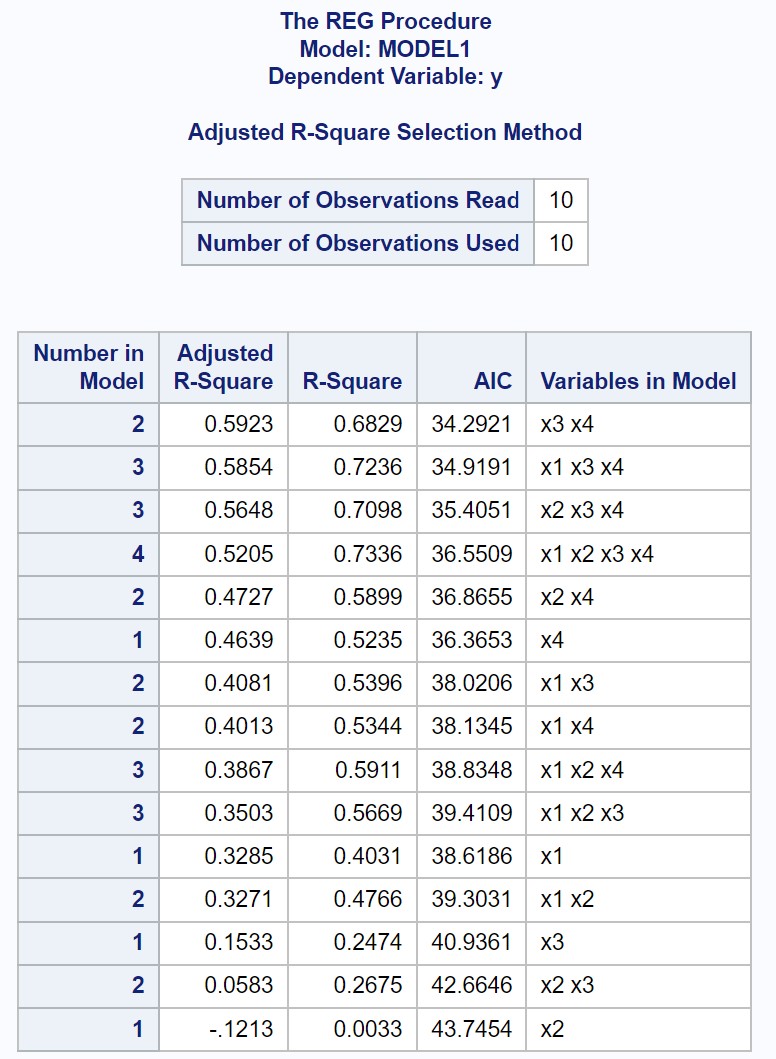
La sortie affiche les valeurs R-carré et AIC ajustées pour chaque modèle de régression linéaire multiple possible.

À partir du résultat, nous pouvons voir que la valeur avec la valeur R carré ajustée la plus élevée et la valeur AIC la plus basse est le modèle de régression qui utilise uniquement x3 et x4 comme variables prédictives.

Ainsi, nous déclarons que le modèle suivant est « le meilleur » parmi tous les modèles possibles :

y = b ₀ + b ₁ (x3) + b ₂ (x4)

Ce modèle de régression particulier a les métriques suivantes :

• Valeur R au carré ajustée : 0,5923
• AIC : 34.2921

Notes sur la sélection du « meilleur » modèle de régression

Notez que parfois, le modèle avec la valeur R carré ajustée la plus élevée n’a pas toujours également la valeur AIC la plus basse.

Lorsqu’il s’agit de décider quel modèle de régression est le meilleur, le R au carré ajusté et l’AIC servent de suggestions, mais dans le monde réel, vous devrez peut-être utiliser l’expertise du domaine pour déterminer quel modèle est le meilleur.

Il peut également être judicieux de choisir un modèle parcimonieux , c’est-à-dire un modèle qui atteint un niveau souhaité d’ajustement en utilisant le moins de variables prédictives possible.

Le raisonnement derrière ce type de modèle découle de l’idée du rasoir d’Occam (parfois appelé « principe de parcimonie ») qui dit que l’explication la plus simple est probablement la bonne.

Appliqué aux statistiques, un modèle qui a peu de paramètres mais atteint un niveau d’ajustement satisfaisant doit être préféré à un modèle qui a une tonne de paramètres et n’atteint qu’un niveau d’ajustement légèrement supérieur.

Ressources additionnelles

Les didacticiels suivants expliquent comment effectuer d’autres tâches courantes dans SAS :

Comment effectuer une régression linéaire simple dans SAS
Comment effectuer une régression linéaire multiple dans SAS
Comment effectuer une régression polynomiale dans SAS
Comment effectuer une régression logistique dans SAS