Une introduction à la régression polynomiale
Lorsque nous disposons d’un ensemble de données avec une variable prédictive et une variable de réponse , nous utilisons souvent une régression linéaire simple pour quantifier la relation entre les deux variables.
Cependant, la régression linéaire simple (SLR) suppose que la relation entre le prédicteur et la variable de réponse est linéaire. Écrit en notation mathématique, SLR suppose que la relation prend la forme :
Y = β 0 + β 1 X + ε
Mais en pratique, la relation entre les deux variables peut en réalité être non linéaire et tenter d’utiliser la régression linéaire peut aboutir à un modèle mal ajusté.
Une façon de prendre en compte une relation non linéaire entre le prédicteur et la variable de réponse consiste à utiliser la régression polynomiale , qui prend la forme :
Y = β 0 + β 1 X + β 2 X 2 + … + β h X h + ε
Dans cette équation, h est appelé degré du polynôme.
À mesure que nous augmentons la valeur de h , le modèle est capable de mieux s’adapter aux relations non linéaires, mais en pratique, nous choisissons rarement que h soit supérieur à 3 ou 4. Au-delà de ce point, le modèle devient trop flexible et surajuste les données .
Notes techniques
- Bien que la régression polynomiale puisse s’adapter à des données non linéaires, elle est toujours considérée comme une forme de régression linéaire car elle est linéaire dans les coefficients β 1 , β 2 , …, β h .
- La régression polynomiale peut également être utilisée pour plusieurs variables prédictives, mais cela crée des termes d’interaction dans le modèle, ce qui peut rendre le modèle extrêmement complexe si plusieurs variables prédictives sont utilisées.
Quand utiliser la régression polynomiale
Nous utilisons la régression polynomiale lorsque la relation entre un prédicteur et une variable de réponse est non linéaire.
Il existe trois manières courantes de détecter une relation non linéaire :
1. Créez un nuage de points.
Le moyen le plus simple de détecter une relation non linéaire consiste à créer un nuage de points de la variable réponse par rapport à la variable prédictive.
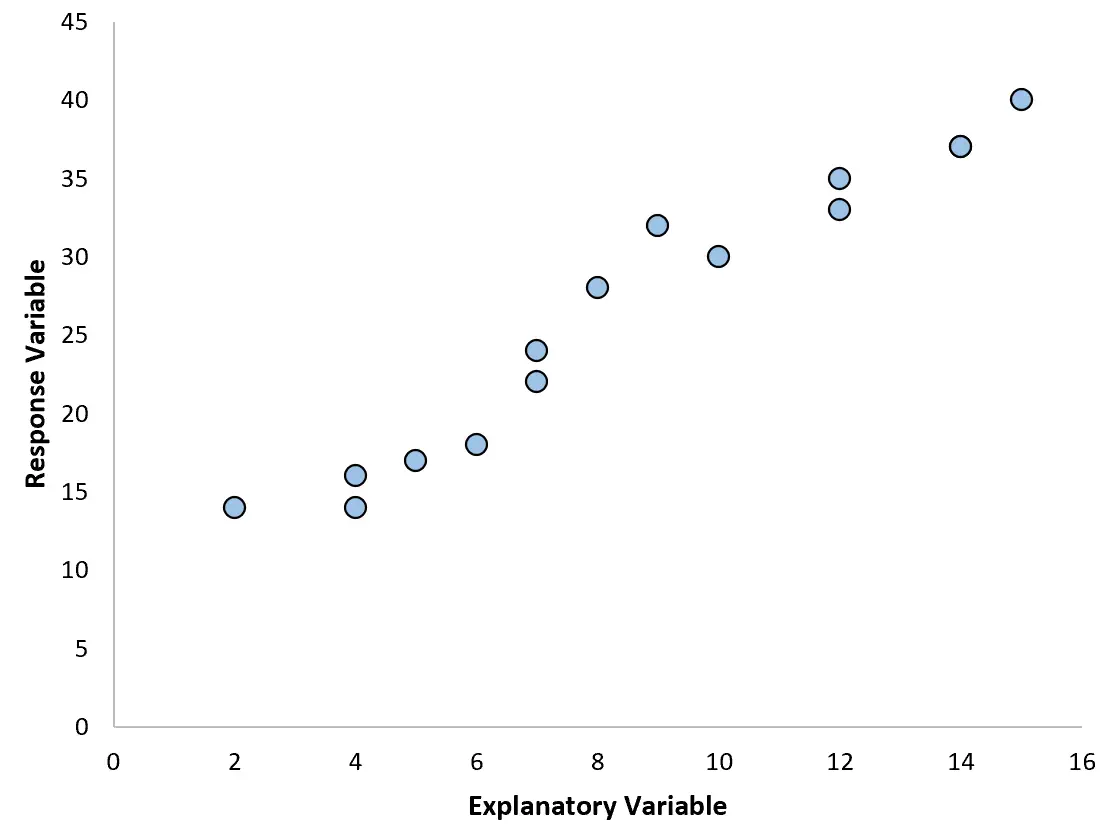
Par exemple, si nous créons le nuage de points suivant, nous pouvons voir que la relation entre les deux variables est à peu près linéaire, donc une simple régression linéaire fonctionnerait probablement correctement sur ces données.
Cependant, si notre nuage de points ressemble à l’un des graphiques suivants, nous pourrions voir que la relation est non linéaire et qu’une régression polynomiale serait donc une bonne idée :
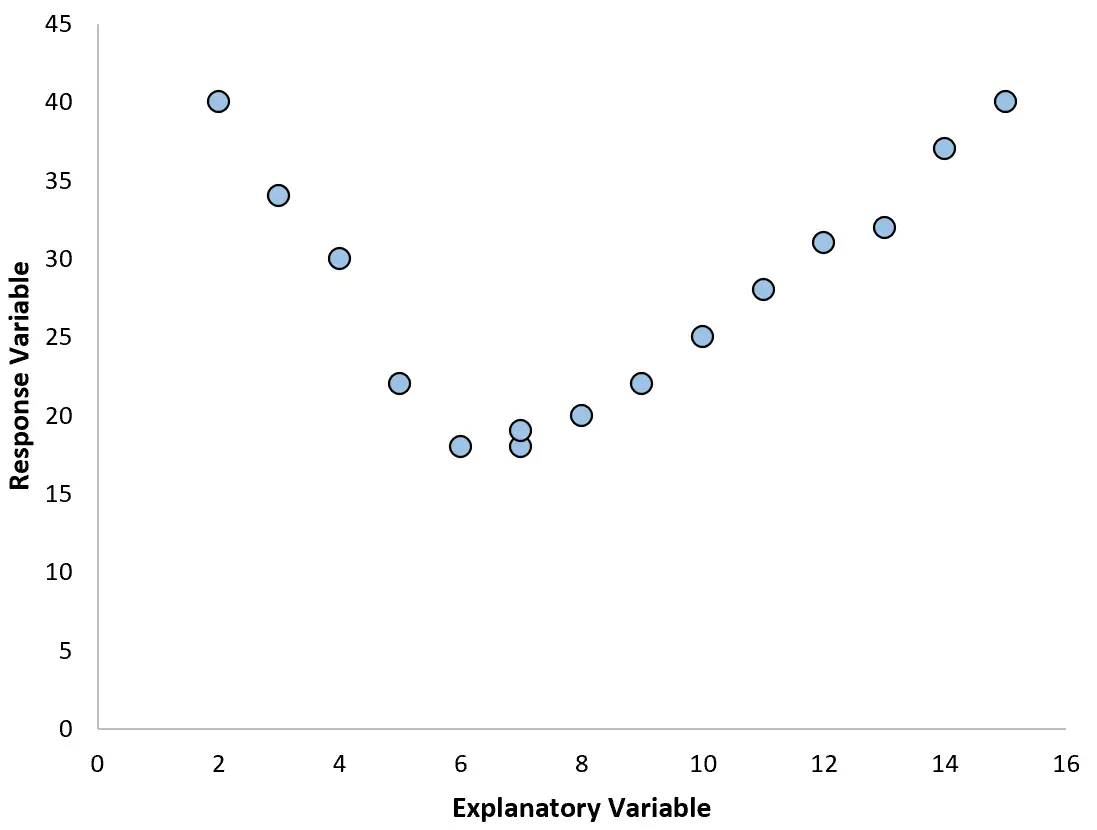
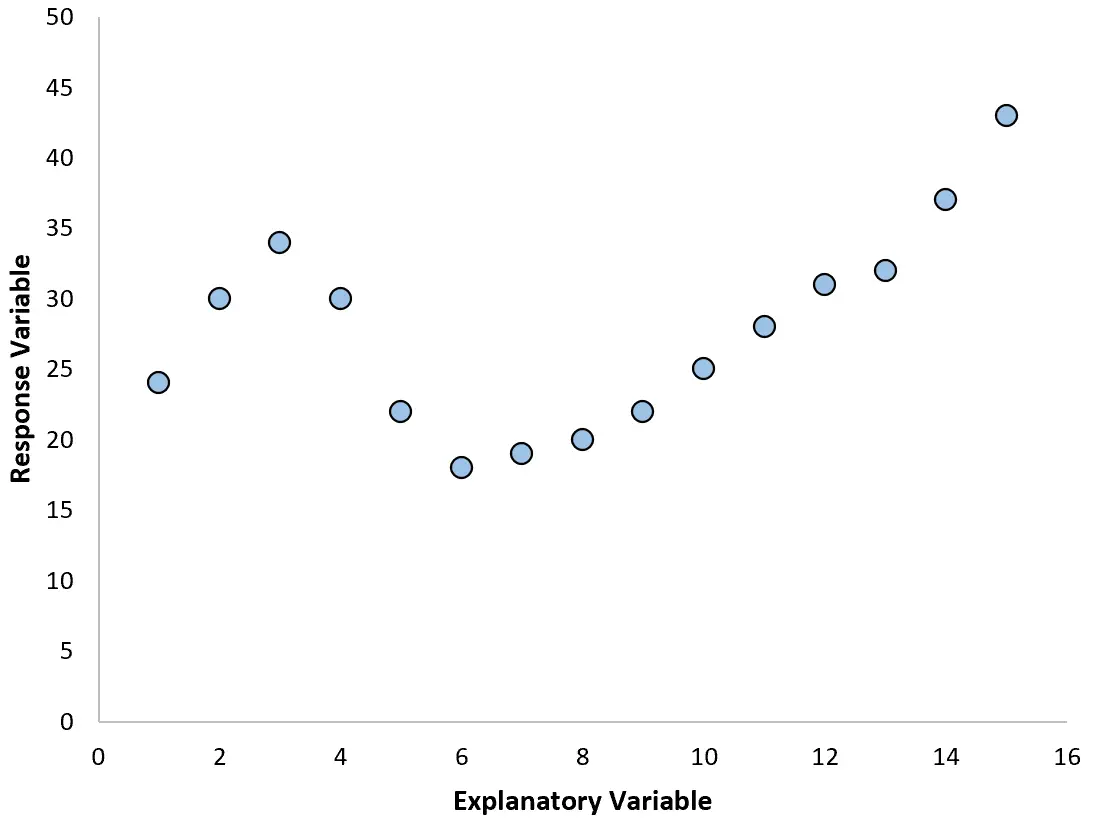
2. Créez un tracé des résidus par rapport au tracé ajusté.
Une autre façon de détecter la non-linéarité consiste à ajuster un modèle de régression linéaire simple aux données, puis à produire un graphique des valeurs résiduelles par rapport aux valeurs ajustées .
Si les résidus du tracé sont répartis à peu près uniformément autour de zéro sans tendance claire, alors une simple régression linéaire est probablement suffisante.
Cependant, si les résidus affichent une tendance non linéaire dans le graphique, cela indique que la relation entre le prédicteur et la réponse est probablement non linéaire.
3. Calculez le R 2 du modèle.
La valeur R 2 d’un modèle de régression vous indique le pourcentage de variation de la variable de réponse qui peut être expliqué par la ou les variables prédictives.
Si vous ajustez un modèle de régression linéaire simple à un ensemble de données et que la valeur R 2 du modèle est assez faible, cela pourrait indiquer que la relation entre le prédicteur et la variable de réponse est plus complexe qu’une simple relation linéaire.
Cela pourrait être le signe que vous devrez peut-être essayer la régression polynomiale à la place.
Connexes :Qu’est-ce qu’une bonne valeur R au carré ?
Comment choisir le degré du polynôme
Un modèle de régression polynomiale prend la forme suivante :
Y = β 0 + β 1 X + β 2 X 2 + … + β h X h + ε
Dans cette équation, h est le degré du polynôme.
Mais comment choisir une valeur pour h ?
En pratique, nous ajustons plusieurs modèles différents avec différentes valeurs de h et effectuons une validation croisée k fois pour déterminer quel modèle produit l’erreur quadratique moyenne (MSE) de test la plus faible.
Par exemple, nous pouvons adapter les modèles suivants à un ensemble de données donné :
- Y = β 0 + β 1 X
- Y = β 0 + β 1 X + β 2 X 2
- Y = β 0 + β 1 X + β 2 X 2 + β 3 X 3
- Y = β 0 + β 1 X + β 2 X 2 + β 3 X 3 + β 4 X 4
Nous pouvons ensuite utiliser la validation croisée k fois pour calculer le test MSE de chaque modèle, ce qui nous indiquera les performances de chaque modèle sur des données qu’il n’a jamais vues auparavant.
Le compromis biais-variance de la régression polynomiale
Il existe un compromis biais-variance lors de l’utilisation de la régression polynomiale. À mesure que nous augmentons le degré du polynôme, le biais diminue (à mesure que le modèle devient plus flexible) mais la variance augmente.
Comme pour tous les modèles d’apprentissage automatique, nous devons trouver un compromis optimal entre biais et variance.
Dans la plupart des cas, cela permet d’augmenter le degré du polynôme dans une certaine mesure, mais au-delà d’une certaine valeur, le modèle commence à s’adapter au bruit des données et le MSE du test commence à diminuer.
Pour garantir que nous ajustons un modèle flexible mais pas trop flexible, nous utilisons la validation croisée k fois pour trouver le modèle qui produit le MSE de test le plus bas.
Comment effectuer une régression polynomiale
Les didacticiels suivants fournissent des exemples de la façon d’effectuer une régression polynomiale dans différents logiciels :
Comment effectuer une régression polynomiale dans Excel
Comment effectuer une régression polynomiale dans R
Comment effectuer une régression polynomiale en Python
