Régression polynomiale dans Google Sheets (étape par étape)
L’analyse de régression est utilisée pour quantifier la relation entre une ou plusieurs variables prédictives et une variable de réponse .
Le type d’analyse de régression le plus courant est la régression linéaire simple , utilisée lorsqu’une variable prédictive et une variable de réponse ont une relation linéaire.
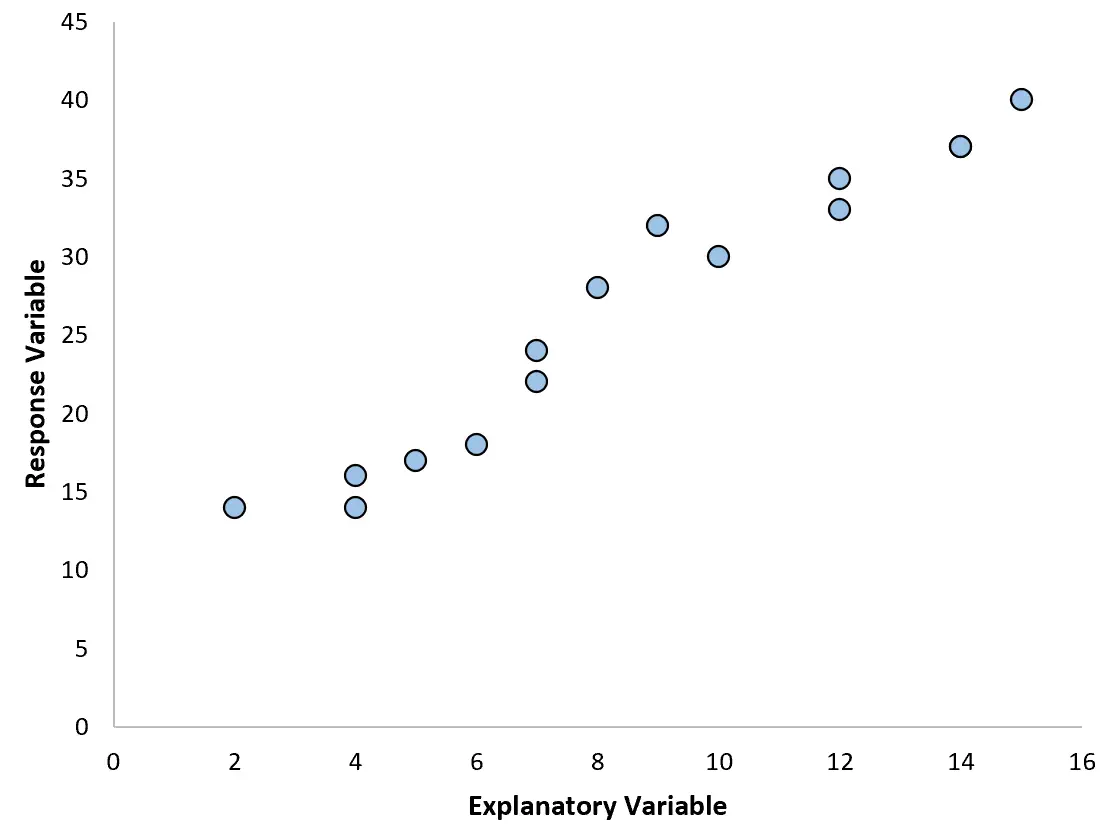
Cependant, il arrive parfois que la relation entre une variable prédictive et une variable de réponse soit non linéaire.
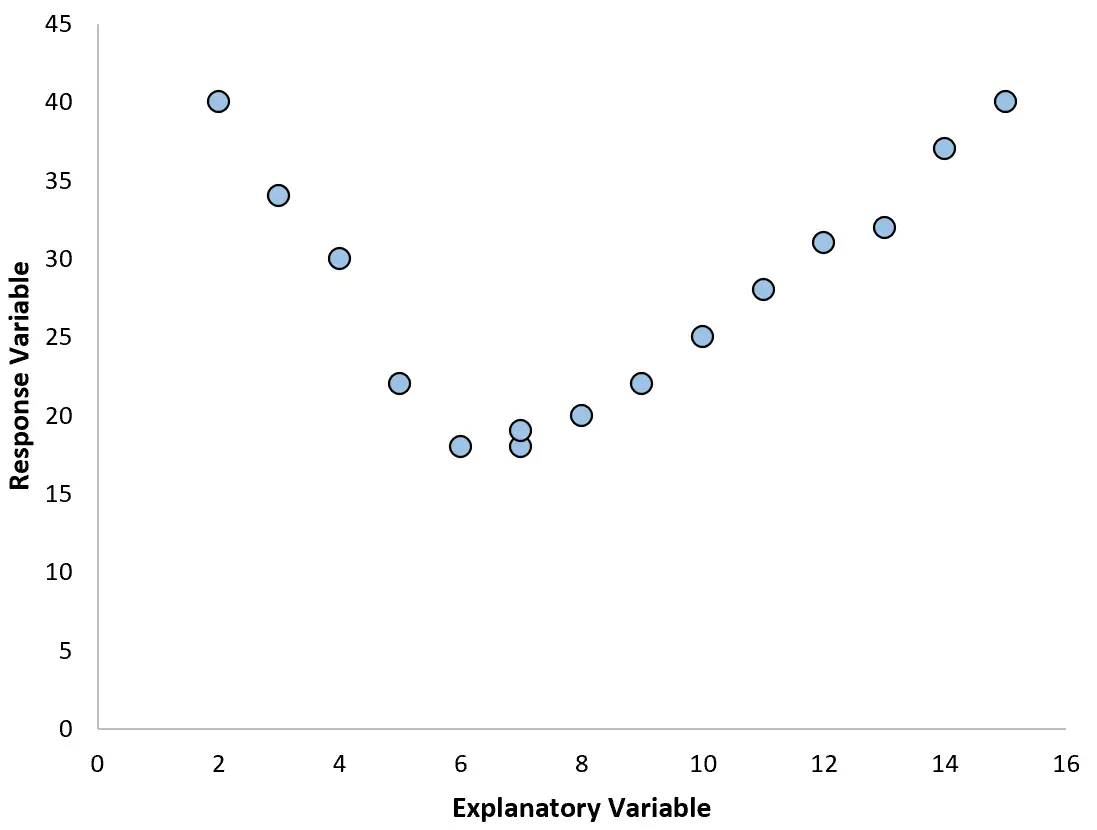
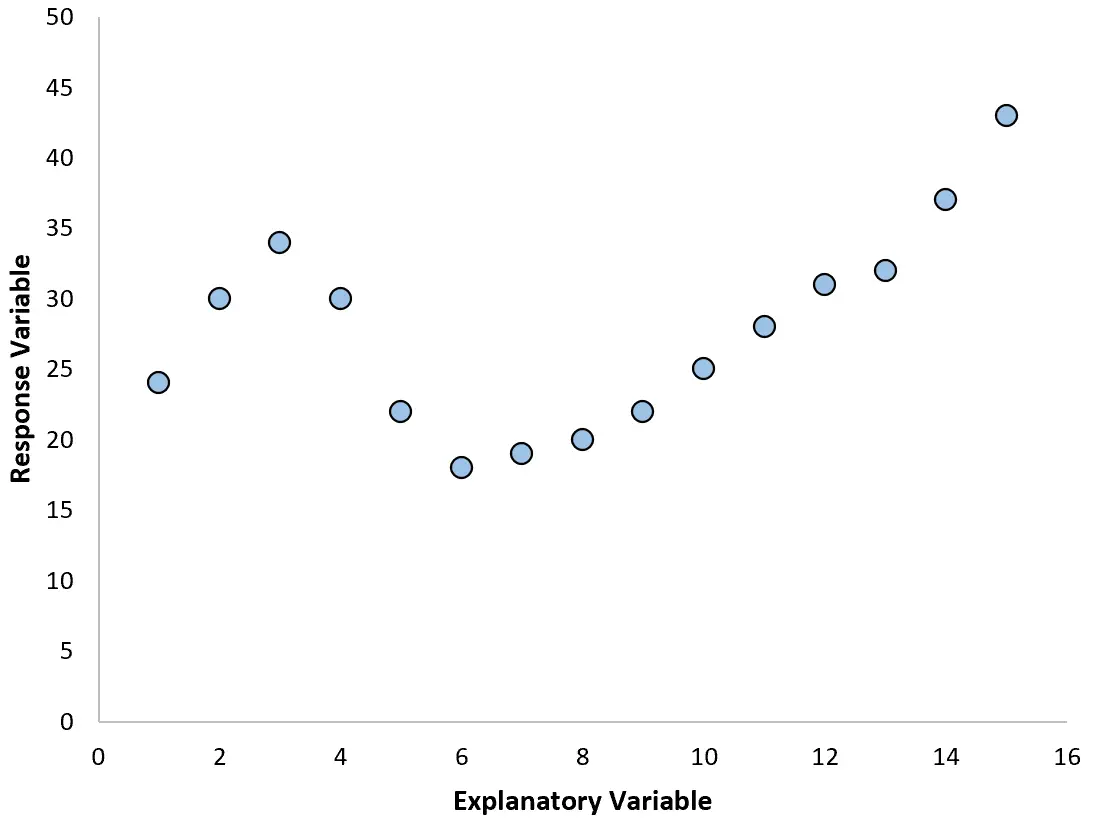
Dans ces cas, il est logique d’utiliser la régression polynomiale , qui peut rendre compte de la relation non linéaire entre les variables.
Ce didacticiel fournit un exemple étape par étape de la façon d’effectuer une régression polynomiale dans Google Sheets.
Étape 1 : Créer les données
Tout d’abord, créons un faux ensemble de données avec les valeurs suivantes :
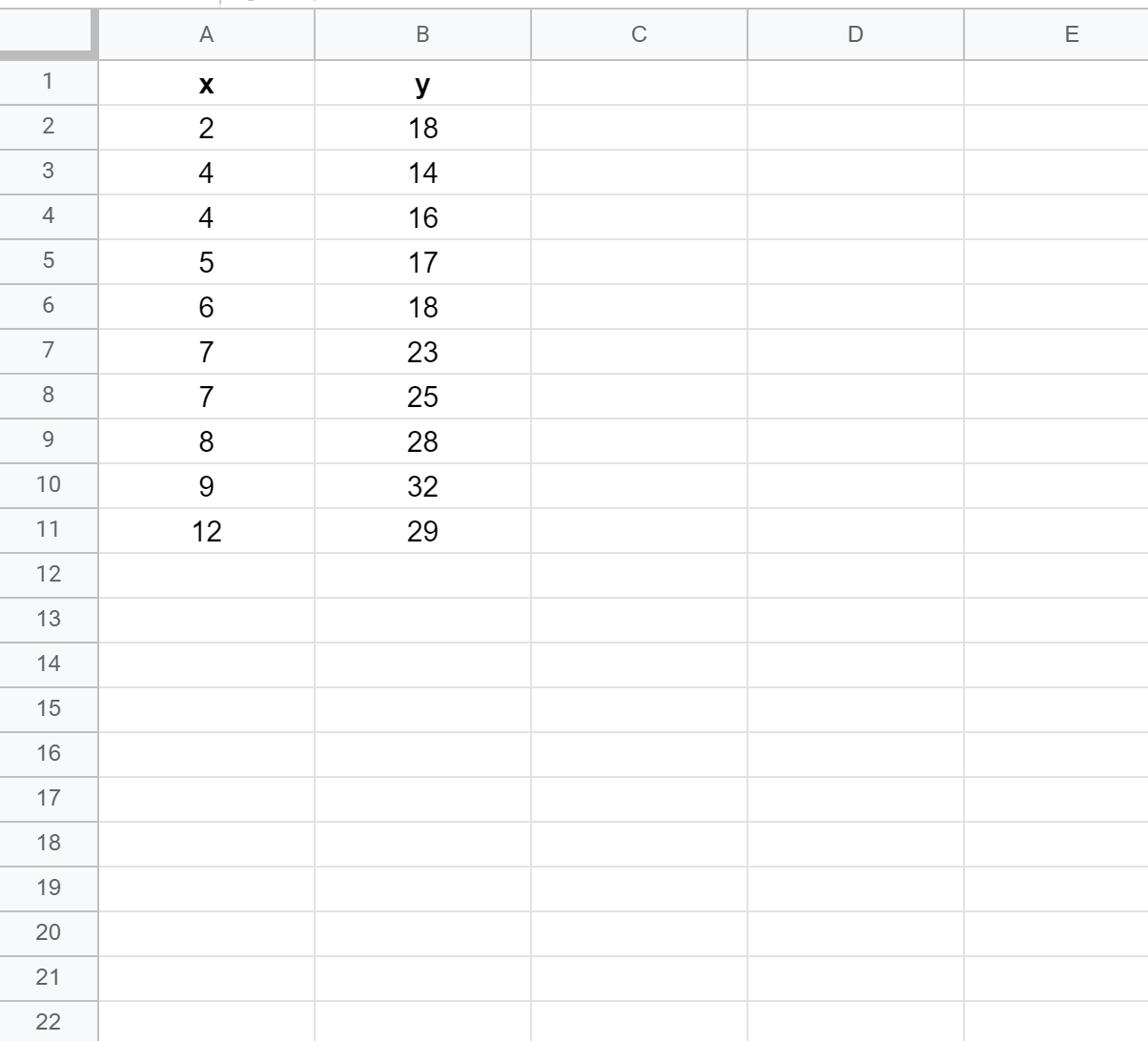
Étape 2 : Créer un nuage de points
Ensuite, nous allons créer un nuage de points pour visualiser les données.
Tout d’abord, mettez en surbrillance les cellules A2:B11 comme suit :
Ensuite, cliquez sur l’onglet Insérer , puis sur Graphique dans le menu déroulant :
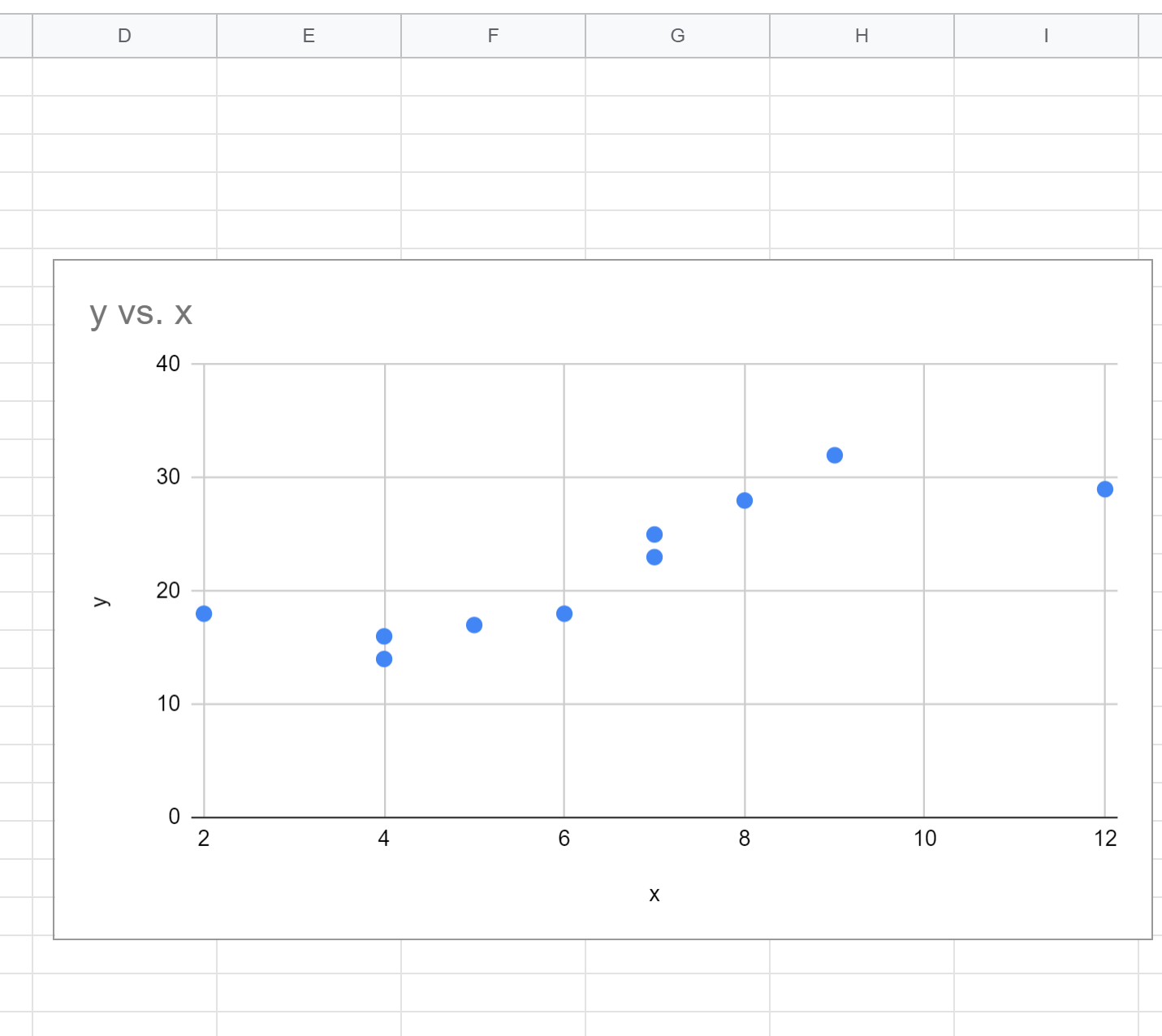
Par défaut, Google Sheets insérera un nuage de points :
Étape 3 : Trouver l’équation de régression polynomiale
Ensuite, double-cliquez n’importe où sur le nuage de points pour afficher la fenêtre de l’éditeur de graphiques sur la droite :
Ensuite, cliquez sur Série . Ensuite, faites défiler vers le bas et cochez la case à côté de Trendline et modifiez le Type en Polynomial . Pour Étiquette, choisissez Utiliser l’équation , puis cochez la case en regard de Afficher R 2 .
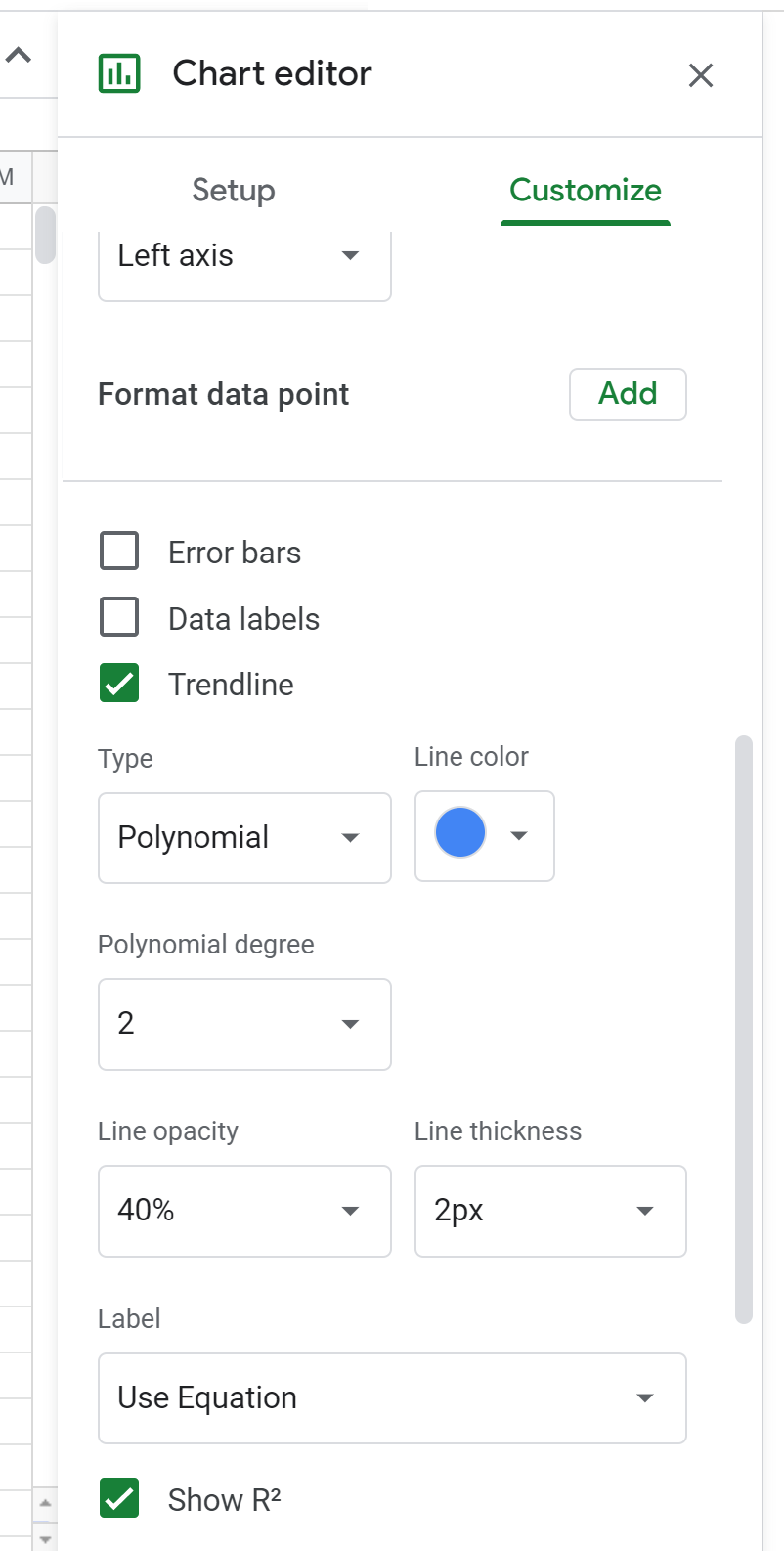
Cela entraînera l’affichage de la formule suivante au-dessus du nuage de points :
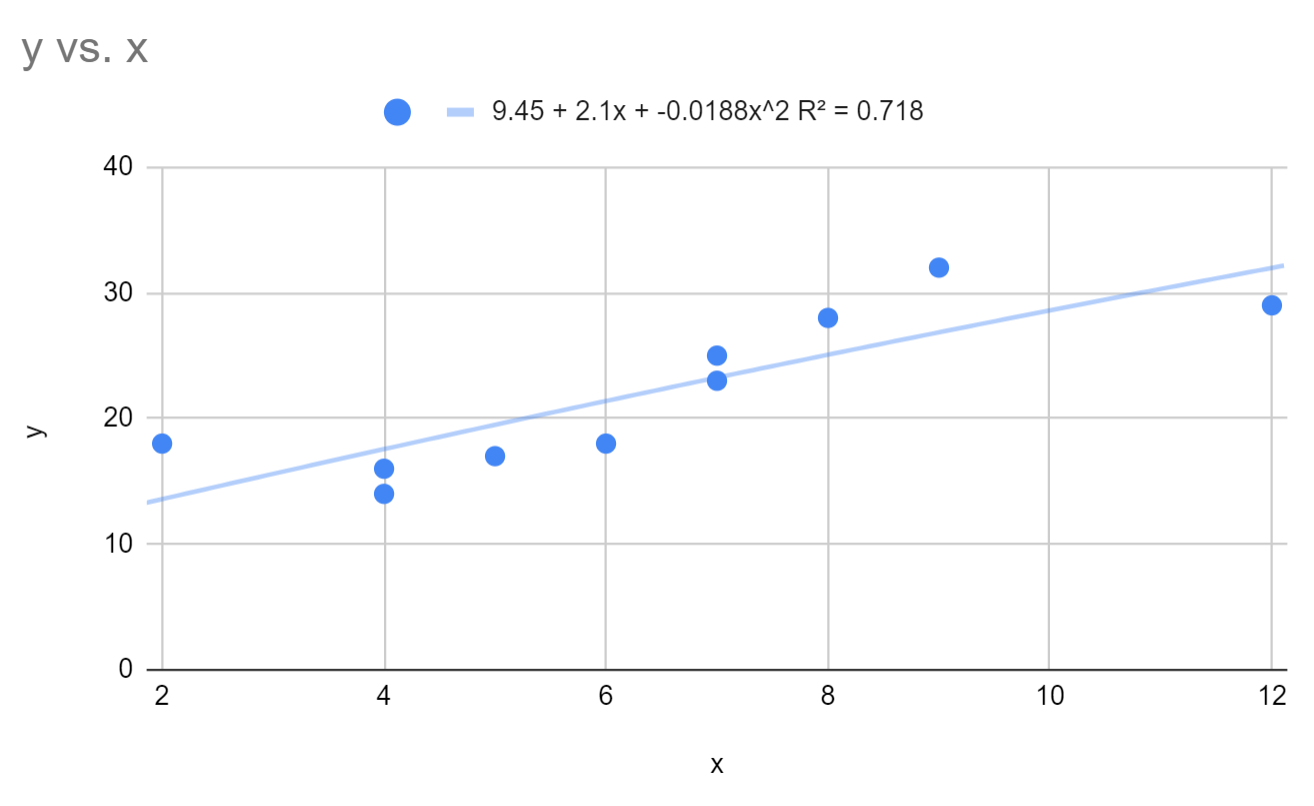
Nous pouvons voir que l’équation de régression polynomiale ajustée est :
y = 9,45 + 2,1x – 0,0188x 2
Le R au carré pour ce modèle est de 0,718 .
Rappelons que R au carré nous indique le pourcentage de variation de la variable de réponse qui peut être expliqué par les variables prédictives. Plus la valeur est élevée, meilleur est le modèle.
Ensuite, changez le degré du polynôme en 3 dans l’éditeur de graphiques :
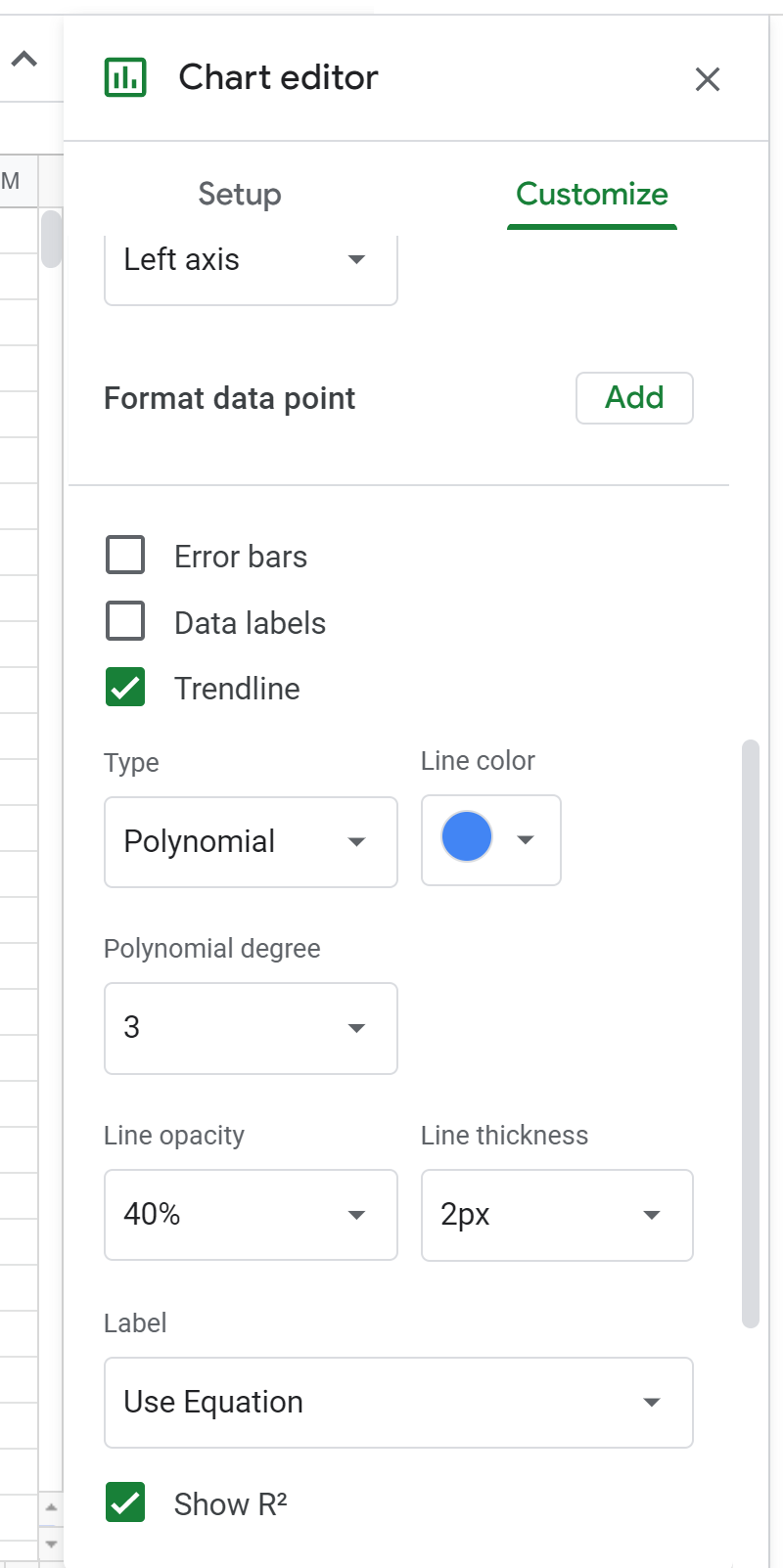
Cela entraînera l’affichage de la formule suivante au-dessus du nuage de points :
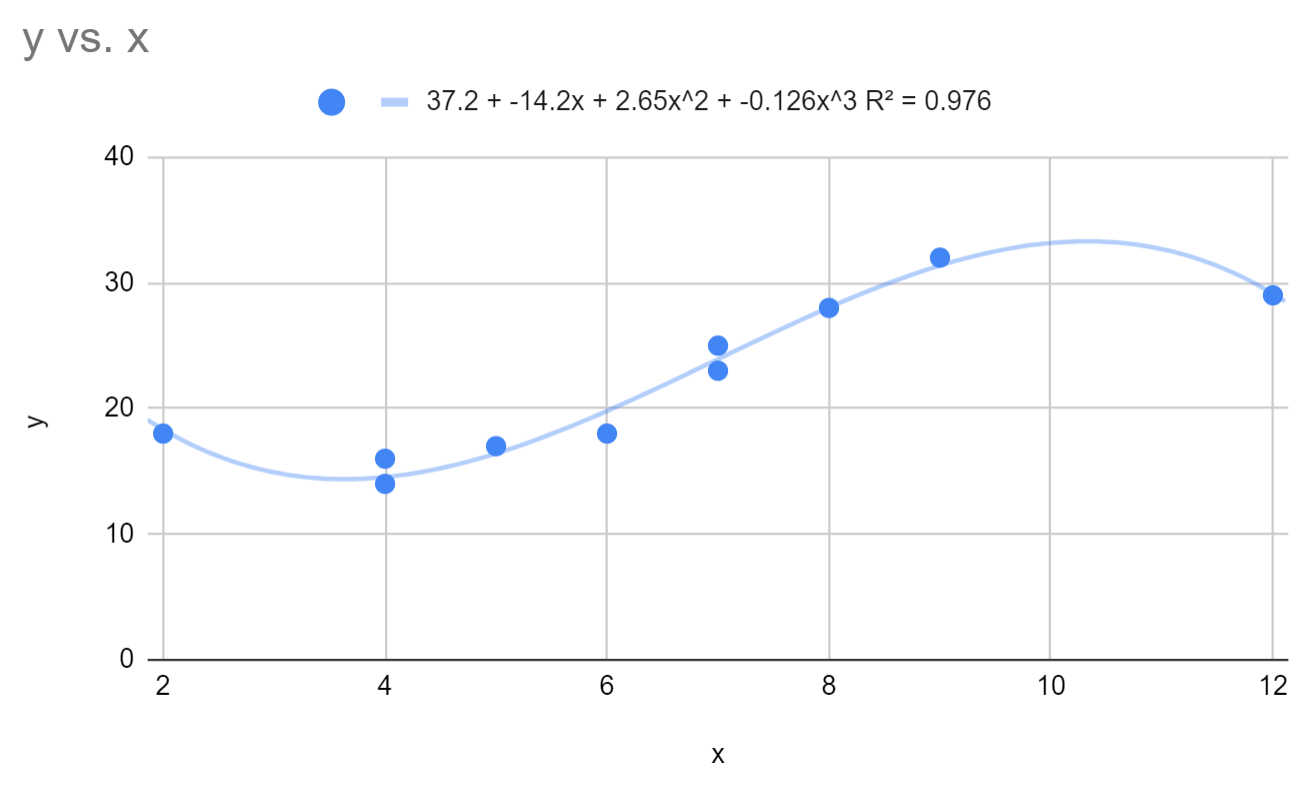
Cela fait changer l’équation de régression polynomiale ajustée en :
y = 37,2 – 14,2x + 2,64x 2 – 0,126x 3
Le R au carré pour ce modèle est de 0,976 .
Notez que le R au carré de ce modèle est nettement supérieur à celui du modèle de régression polynomiale avec un degré de 2. Cela suggère que ce modèle de régression est nettement meilleur pour capturer la tendance des données sous-jacentes.
Si vous modifiez le degré du polynôme à 4, le R au carré augmente à peine jusqu’à 0,981 . Cela suggère qu’un modèle de régression polynomiale de degré 3 est suffisant pour capturer la tendance de ces données.
Nous pouvons utiliser l’équation de régression ajustée pour trouver la valeur attendue de la variable de réponse en fonction d’une valeur donnée de la variable prédictive. Par exemple, si x = 4 alors la valeur attendue pour y serait :
y = 37,2 – 14,2(4) + 2,64(4) 2 – 0,126(4) 3 = 14,576
Vous pouvez trouver d’autres didacticiels Google Sheets sur cette page .
