Comment effectuer une régression polynomiale en Python

L’analyse de régression est utilisée pour quantifier la relation entre une ou plusieurs variables explicatives et une variable de réponse.

Le type d’analyse de régression le plus courant est la régression linéaire simple , utilisée lorsqu’une variable prédictive et une variable de réponse ont une relation linéaire.

Cependant, il arrive parfois que la relation entre une variable prédictive et une variable de réponse soit non linéaire.

Par exemple, la vraie relation peut être quadratique :

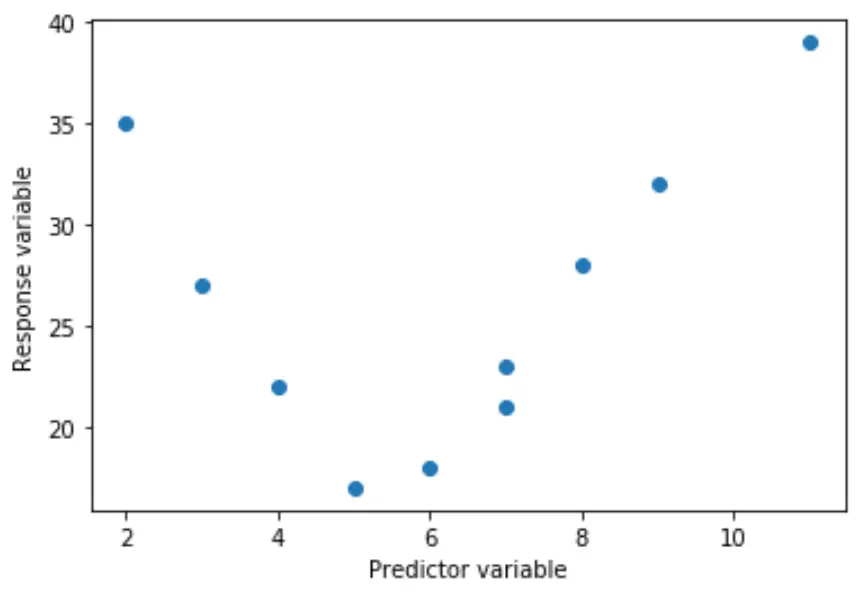
Ou il peut être cubique :

Dans ces cas, il est logique d’utiliser la régression polynomiale , qui peut rendre compte de la relation non linéaire entre les variables.

Ce didacticiel explique comment effectuer une régression polynomiale en Python.

Exemple : régression polynomiale en Python

Supposons que nous ayons la variable prédictive (x) et la variable de réponse (y) suivantes en Python :

x = [2, 3, 4, 5, 6, 7, 7, 8, 9, 11, 12]
y = [18, 16, 15, 17, 20, 23, 25, 28, 31, 30, 29]

Si nous créons un simple nuage de points de ces données, nous pouvons voir que la relation entre x et y n’est clairement pas linéaire :

import matplotlib.pyplot as plt

#create scatterplot 
plt.scatter(x, y)

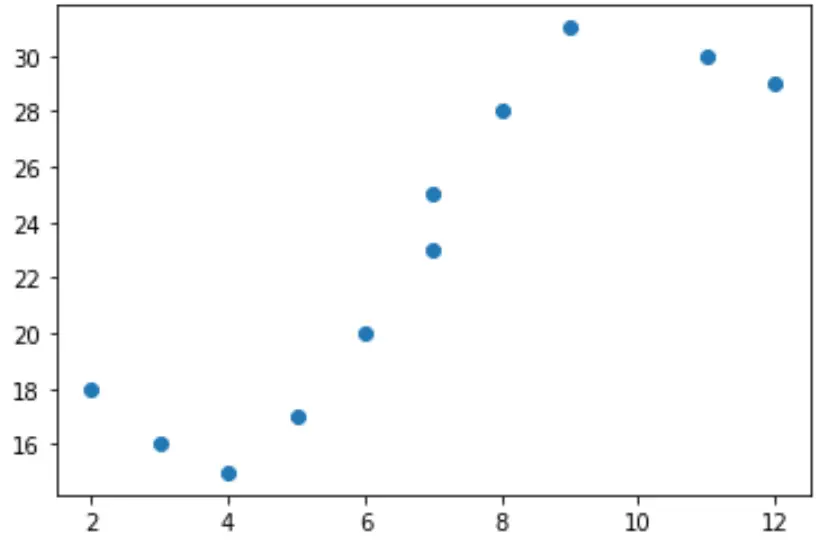
Il ne serait donc pas logique d’adapter un modèle de régression linéaire à ces données. Au lieu de cela, nous pouvons tenter d’ajuster un modèle de régression polynomiale avec un degré de 3 en utilisant la fonction numpy.polyfit() :

import numpy as np

#polynomial fit with degree = 3
model = np.poly1d(np.polyfit(x, y, 3))

#add fitted polynomial line to scatterplot
polyline = np.linspace(1, 12, 50)
plt.scatter(x, y)
plt.plot(polyline, model(polyline))
plt.show()

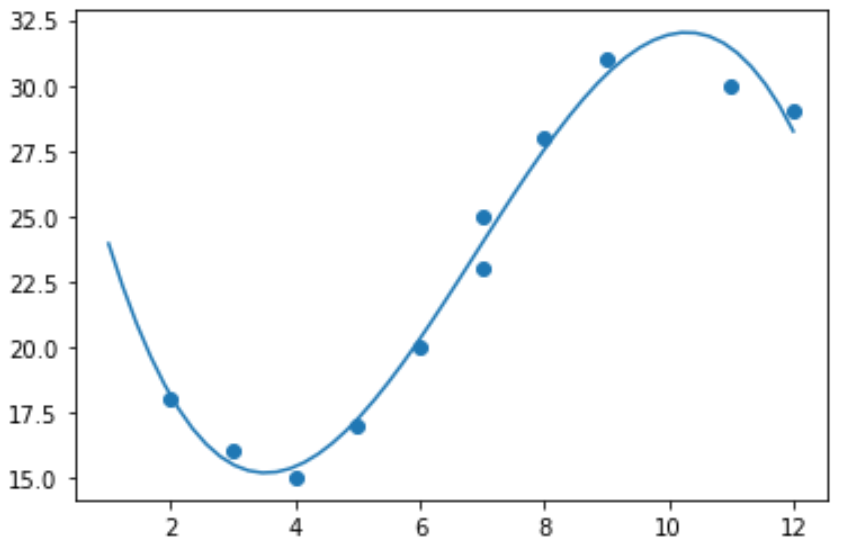
Nous pouvons obtenir l’équation de régression polynomiale ajustée en imprimant les coefficients du modèle :

print(model)

poly1d([ -0.10889554,   2.25592957, -11.83877127,  33.62640038])

L’équation de régression polynomiale ajustée est la suivante :

y = -0,109x ³ + 2,256x ² – 11,839x + 33,626

Cette équation peut être utilisée pour trouver la valeur attendue de la variable de réponse en fonction d’une valeur donnée de la variable explicative.

Par exemple, supposons que x = 4. La valeur attendue pour la variable de réponse, y, serait :

y = -0,109(4) ³ + 2,256(4) ² – 11,839(4) + 33,626= 15,39 .

Nous pouvons également écrire une courte fonction pour obtenir le R au carré du modèle, qui est la proportion de la variance de la variable de réponse qui peut être expliquée par les variables prédictives.

#define function to calculate r-squared
def polyfit(x, y, degree):
    results = {}
    coeffs = numpy.polyfit(x, y, degree)
    p = numpy.poly1d(coeffs)
    #calculate r-squared
    yhat = p(x)
    ybar = numpy.sum(y)/len(y)
    ssreg = numpy.sum((yhat-ybar)**2)
    sstot = numpy.sum((y - ybar)**2)
    results['r_squared'] = ssreg / sstot

    return results

#find r-squared of polynomial model with degree = 3
polyfit(x, y, 3)

{'r_squared': 0.9841113454245183}

Dans cet exemple, le R carré du modèle est 0,9841 .

Cela signifie que 98,41 % de la variation de la variable de réponse peut être expliquée par les variables prédictives.