Régression polynomiale dans R (étape par étape)
La régression polynomiale est une technique que nous pouvons utiliser lorsque la relation entre une variable prédictive et une variable de réponse est non linéaire.
Ce type de régression prend la forme :
Y = β 0 + β 1 X + β 2 X 2 + … + β h X h + ε
où h est le « degré » du polynôme.
Ce didacticiel fournit un exemple étape par étape de la façon d’effectuer une régression polynomiale dans R.
Étape 1 : Créer les données
Pour cet exemple, nous allons créer un ensemble de données contenant le nombre d’heures étudiées et la note de l’examen final pour une classe de 50 étudiants :
#make this example reproducible set.seed(1) #create dataset df <- data.frame(hours = runif(50, 5, 15), score=50) df$score = df$score + df$hours^3/150 + df$hours*runif(50, 1, 2) #view first six rows of data head(data) hours score 1 7.655087 64.30191 2 8.721239 70.65430 3 10.728534 73.66114 4 14.082078 86.14630 5 7.016819 59.81595 6 13.983897 83.60510
Étape 2 : Visualisez les données
Avant d’adapter un modèle de régression aux données, créons d’abord un nuage de points pour visualiser la relation entre les heures étudiées et la note de l’examen :
library(ggplot2) ggplot(df, aes(x=hours, y=score)) + geom_point()
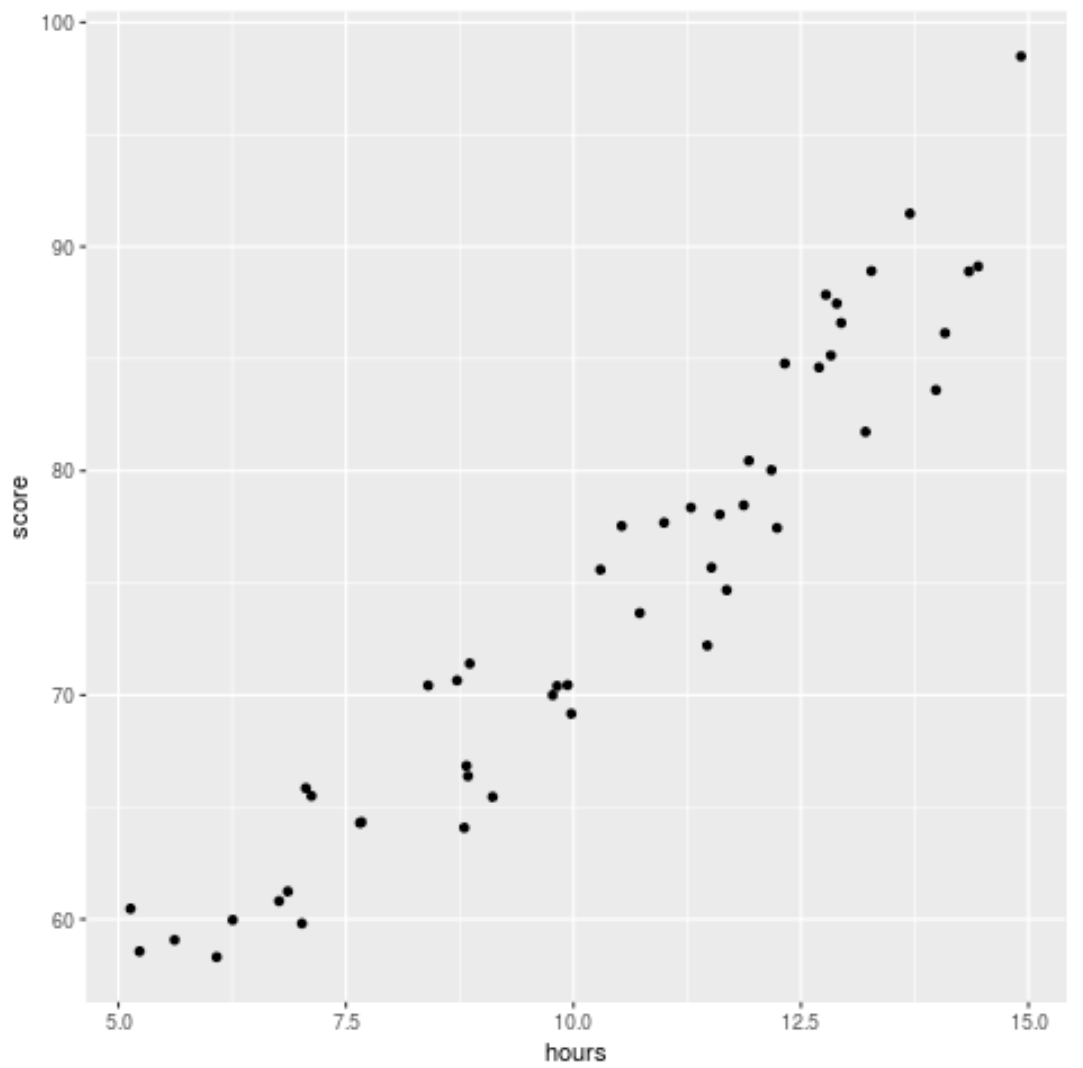
Nous pouvons voir que les données présentent une relation légèrement quadratique, ce qui indique que la régression polynomiale pourrait mieux s’adapter aux données que la simple régression linéaire.
Étape 3 : Ajuster les modèles de régression polynomiale
Ensuite, nous ajusterons cinq modèles de régression polynomiale différents avec des degrés h = 1…5 et utiliserons la validation croisée k fois avec k = 10 fois pour calculer le MSE de test pour chaque modèle :
#randomly shuffle data
df.shuffled <- df[sample(nrow(df)),]
#define number of folds to use for k-fold cross-validation
K <- 10
#define degree of polynomials to fit
degree <- 5
#create k equal-sized folds
folds <- cut(seq(1,nrow(df.shuffled)),breaks=K,labels=FALSE)
#create object to hold MSE's of models
mse = matrix(data=NA,nrow=K,ncol=degree)
#Perform K-fold cross validation
for(i in 1:K){
#define training and testing data
testIndexes <- which(folds==i,arr.ind=TRUE)
testData <- df.shuffled[testIndexes, ]
trainData <- df.shuffled[-testIndexes, ]
#use k-fold cv to evaluate models
for (j in 1:degree){
fit.train = lm(score ~ poly(hours,j), data=trainData)
fit.test = predict(fit.train, newdata=testData)
mse[i,j] = mean((fit.test-testData$score)^2)
}
}
#find MSE for each degree
colMeans(mse)
[1] 9.802397 8.748666 9.601865 10.592569 13.545547
À partir du résultat, nous pouvons voir le test MSE pour chaque modèle :
- Test MSE avec degré h = 1 : 9,80
- Test MSE avec degré h = 2 : 8,75
- Test MSE avec degré h = 3 : 9,60
- Test MSE avec degré h = 4 : 10,59
- Test MSE avec degré h = 5 : 13,55
Le modèle avec le MSE de test le plus bas s’est avéré être le modèle de régression polynomiale avec un degré h = 2.
Cela correspond à notre intuition du nuage de points d’origine : un modèle de régression quadratique correspond le mieux aux données.
Étape 4 : Analyser le modèle final
Enfin, on peut obtenir les coefficients du modèle le plus performant :
#fit best model best = lm(score ~ poly(hours,2, raw=T), data=df) #view summary of best model summary(best) Call: lm(formula = score ~ poly(hours, 2, raw = T), data = df) Residuals: Min 1Q Median 3Q Max -5.6589 -2.0770 -0.4599 2.5923 4.5122 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 54.00526 5.52855 9.768 6.78e-13 *** poly(hours, 2, raw = T)1 -0.07904 1.15413 -0.068 0.94569 poly(hours, 2, raw = T)2 0.18596 0.05724 3.249 0.00214 ** --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
À partir du résultat, nous pouvons voir que le modèle ajusté final est :
Score = 54,00526 – 0,07904*(heures) + 0,18596*(heures) 2
Nous pouvons utiliser cette équation pour estimer le score qu’un étudiant recevra en fonction du nombre d’heures étudiées.
Par exemple, un étudiant qui étudie 10 heures devrait obtenir une note de 71,81 :
Score = 54,00526 – 0,07904*(10) + 0,18596*(10) 2 = 71,81
Nous pouvons également tracer le modèle ajusté pour voir dans quelle mesure il s’adapte aux données brutes :
ggplot(df, aes(x=hours, y=score)) + geom_point() + stat_smooth(method='lm', formula = y ~ poly(x,2), size = 1) + xlab('Hours Studied') + ylab('Score')
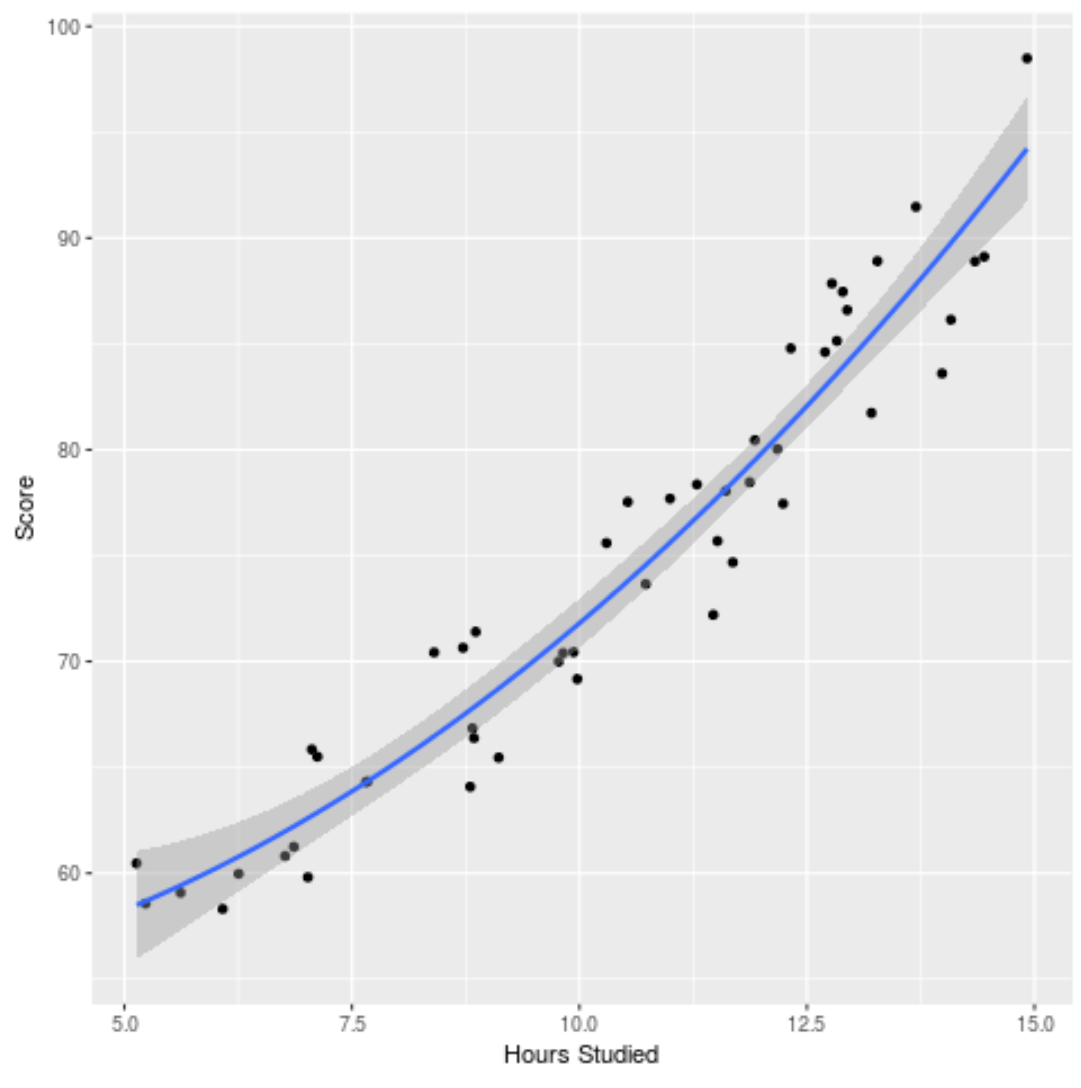
Vous pouvez trouver le code R complet utilisé dans cet exemple ici .
