Comment effectuer une régression polynomiale à l’aide de Scikit-Learn

La régression polynomiale est une technique que nous pouvons utiliser lorsque la relation entre une variable prédictive et une variable de réponse est non linéaire.

Ce type de régression prend la forme :

Y = β ₀ + β ₁ X + β ₂ X ² + … + β _h X ^h + ε

où h est le « degré » du polynôme.

L’exemple étape par étape suivant montre comment effectuer une régression polynomiale en Python à l’aide de sklearn.

Étape 1 : Créer les données

Tout d’abord, créons deux tableaux NumPy pour contenir les valeurs d’un prédicteur et d’une variable de réponse :

import matplotlib.pyplot as plt
import numpy as np

#define predictor and response variables
x = np.array([2, 3, 4, 5, 6, 7, 7, 8, 9, 11, 12])
y = np.array([18, 16, 15, 17, 20, 23, 25, 28, 31, 30, 29])

#create scatterplot to visualize relationship between x and y
plt.scatter(x, y)

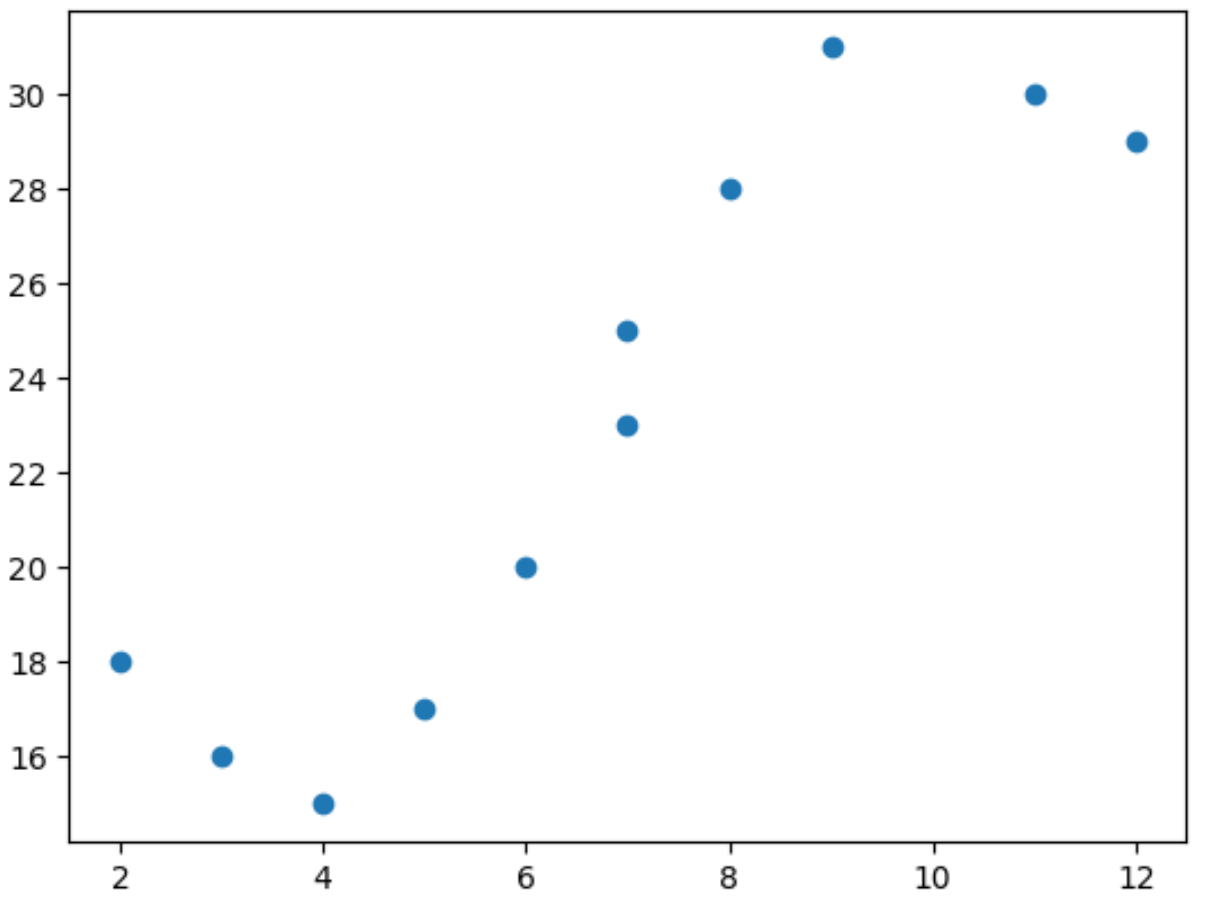
À partir du nuage de points, nous pouvons voir que la relation entre x et y n’est pas linéaire.

C’est donc une bonne idée d’adapter un modèle de régression polynomiale aux données pour capturer la relation non linéaire entre les deux variables.

Étape 2 : Ajuster le modèle de régression polynomiale

Le code suivant montre comment utiliser les fonctions de sklearn pour ajuster un modèle de régression polynomiale d’un degré de 3 à cet ensemble de données :

from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression

#specify degree of 3 for polynomial regression model
#include bias=False means don't force y-intercept to equal zero
poly = PolynomialFeatures(degree=3, include_bias=False)

#reshape data to work properly with sklearn
poly_features = poly.fit_transform(x.reshape(-1, 1))

#fit polynomial regression model
poly_reg_model = LinearRegression()
poly_reg_model.fit(poly_features, y)

#display model coefficients
print(poly_reg_model.intercept_, poly_reg_model.coef_)

33.62640037532282 [-11.83877127   2.25592957  -0.10889554]

En utilisant les coefficients du modèle affichés sur la dernière ligne, nous pouvons écrire l’équation de régression polynomiale ajustée comme suit :

y = -0,109x ³ + 2,256x ² – 11,839x + 33,626

Cette équation peut être utilisée pour trouver la valeur attendue de la variable de réponse en fonction d’une valeur donnée de la variable prédite.

Par exemple, si x vaut 4, la valeur attendue pour la variable de réponse, y, serait 15,39 :

y = -0,109(4) ³ + 2,256(4) ² – 11,839(4) + 33,626= 15,39

Remarque : Pour ajuster un modèle de régression polynomiale avec un degré différent, modifiez simplement la valeur de l’argument degré dans la fonction PolynomialFeatures() .

Étape 3 : Visualisez le modèle de régression polynomiale

Enfin, nous pouvons créer un tracé simple pour visualiser le modèle de régression polynomiale ajusté sur les points de données d’origine :

#use model to make predictions on response variable
y_predicted = poly_reg_model.predict(poly_features)

#create scatterplot of x vs. y
plt.scatter(x, y)

#add line to show fitted polynomial regression model
plt.plot(x, y_predicted, color='purple')

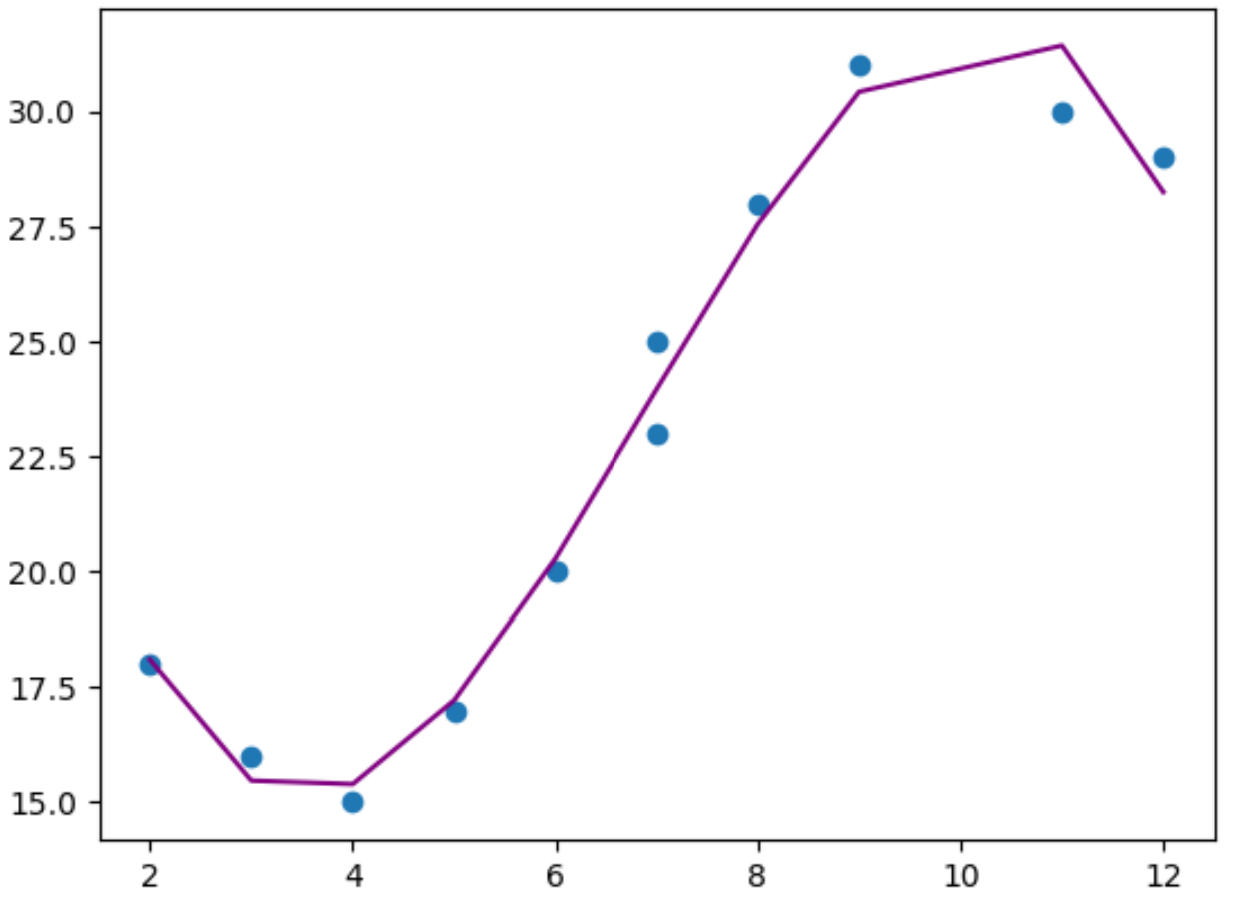
D’après le graphique, nous pouvons voir que le modèle de régression polynomiale semble bien s’adapter aux données sans surajustement .

Remarque : Vous pouvez trouver la documentation complète de la fonction sklearn PolynomialFeatures() ici .

Ressources additionnelles

Les didacticiels suivants expliquent comment effectuer d’autres tâches courantes à l’aide de sklearn :

Comment extraire les coefficients de régression de sklearn
Comment calculer la précision équilibrée à l’aide de sklearn
Comment interpréter le rapport de classification dans Sklearn