Comment effectuer une régression quadratique dans SPSS

Lorsque deux variables ont une relation linéaire, vous pouvez souvent utiliser une simple régression linéaire pour quantifier leur relation.

Cependant, la régression linéaire simple ne fonctionne pas bien lorsque deux variables ont une relation non linéaire. Dans ces cas, vous pouvez essayer d’utiliser la régression quadratique .

Ce didacticiel explique comment effectuer une régression quadratique dans SPSS.

Exemple : régression quadratique dans SPSS

Supposons que nous souhaitions comprendre la relation entre le nombre d’heures travaillées et le bonheur. Nous disposons des données suivantes sur le nombre d’heures travaillées par semaine et le niveau de bonheur déclaré (sur une échelle de 0 à 100) pour 16 personnes différentes :

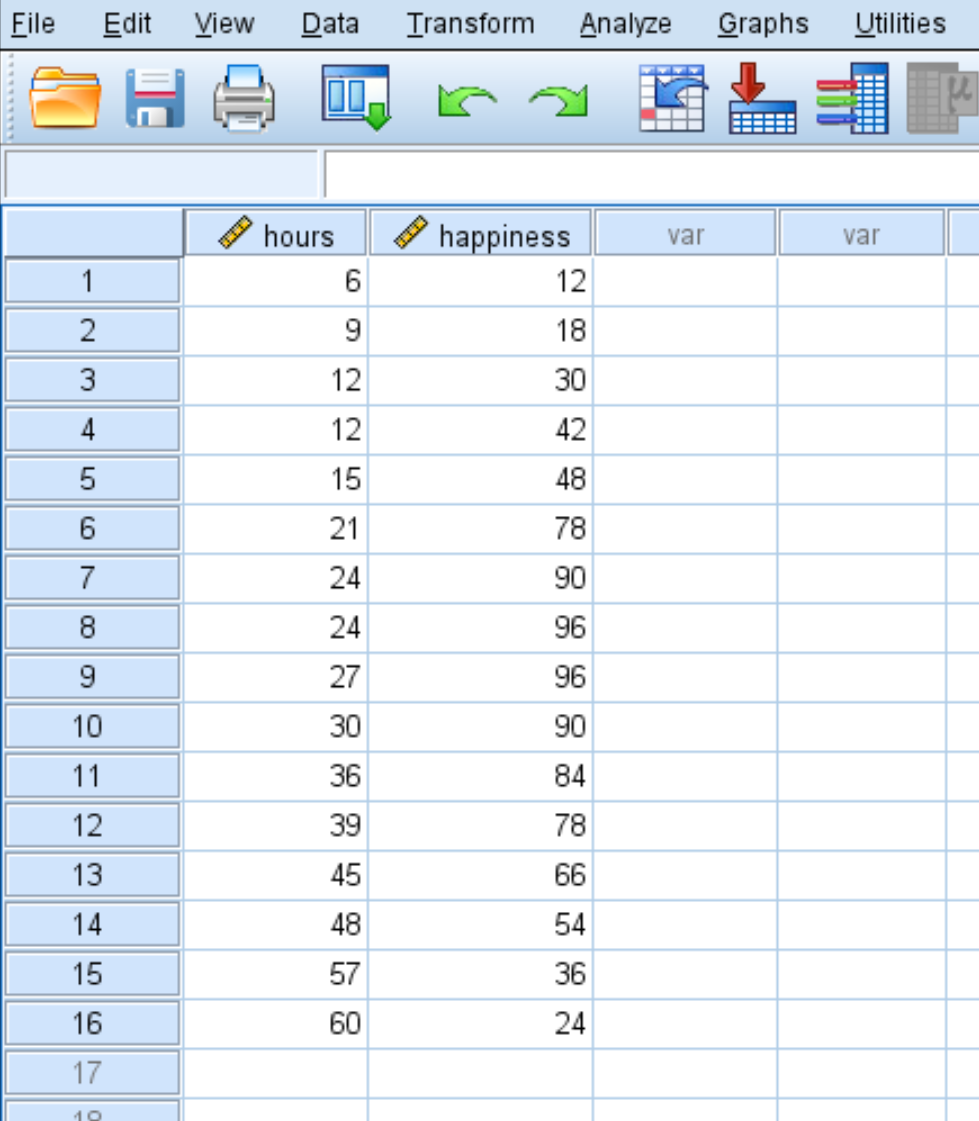
Utilisez les étapes suivantes pour effectuer une régression quadratique dans SPSS.

Étape 1 : Visualisez les données.

Avant d’effectuer une régression quadratique, créons un nuage de points pour visualiser la relation entre les heures travaillées et le bonheur afin de vérifier que les deux variables ont réellement une relation quadratique.

Cliquez sur l’onglet Graphiques , puis sur Chart Builder :

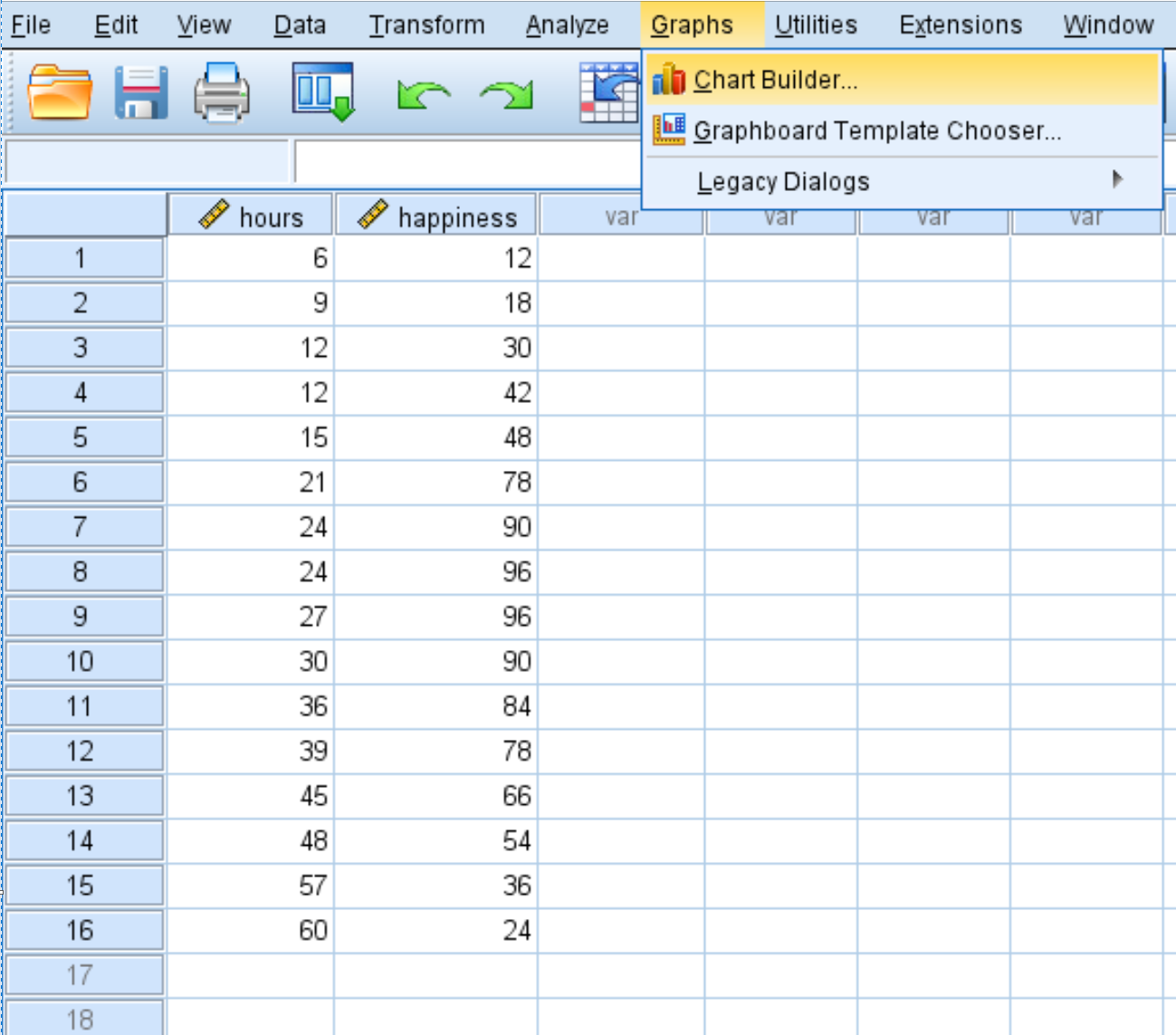
Dans la nouvelle fenêtre qui apparaît, choisissez Scatter/Dot dans la liste Choisir dans . Faites ensuite glisser le graphique intitulé Simple Scatter dans la fenêtre d’édition principale. Faites glisser les heures variables sur l’axe des x et le bonheur sur l’axe des y. Cliquez ensuite sur OK .

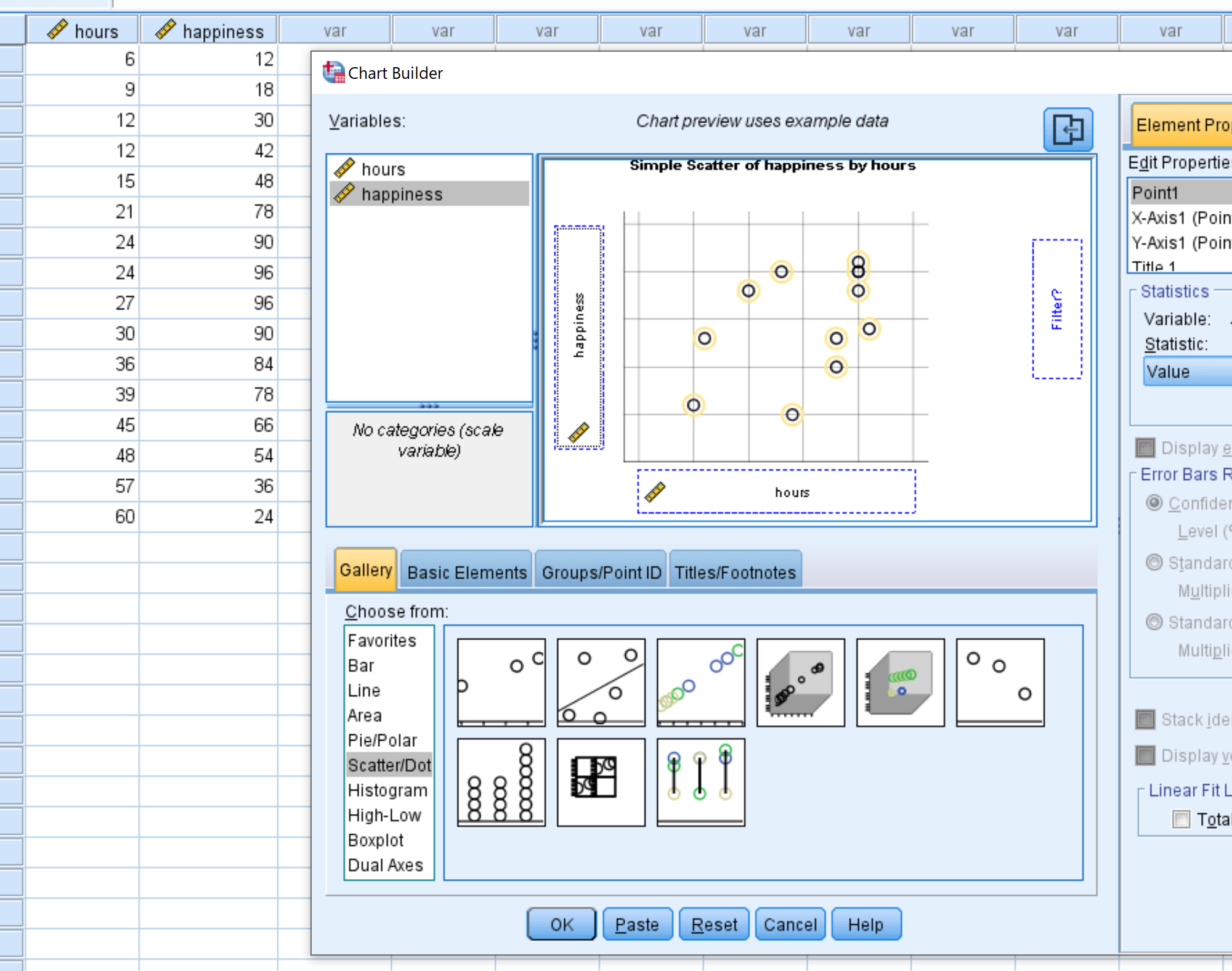
Le nuage de points suivant apparaîtra :

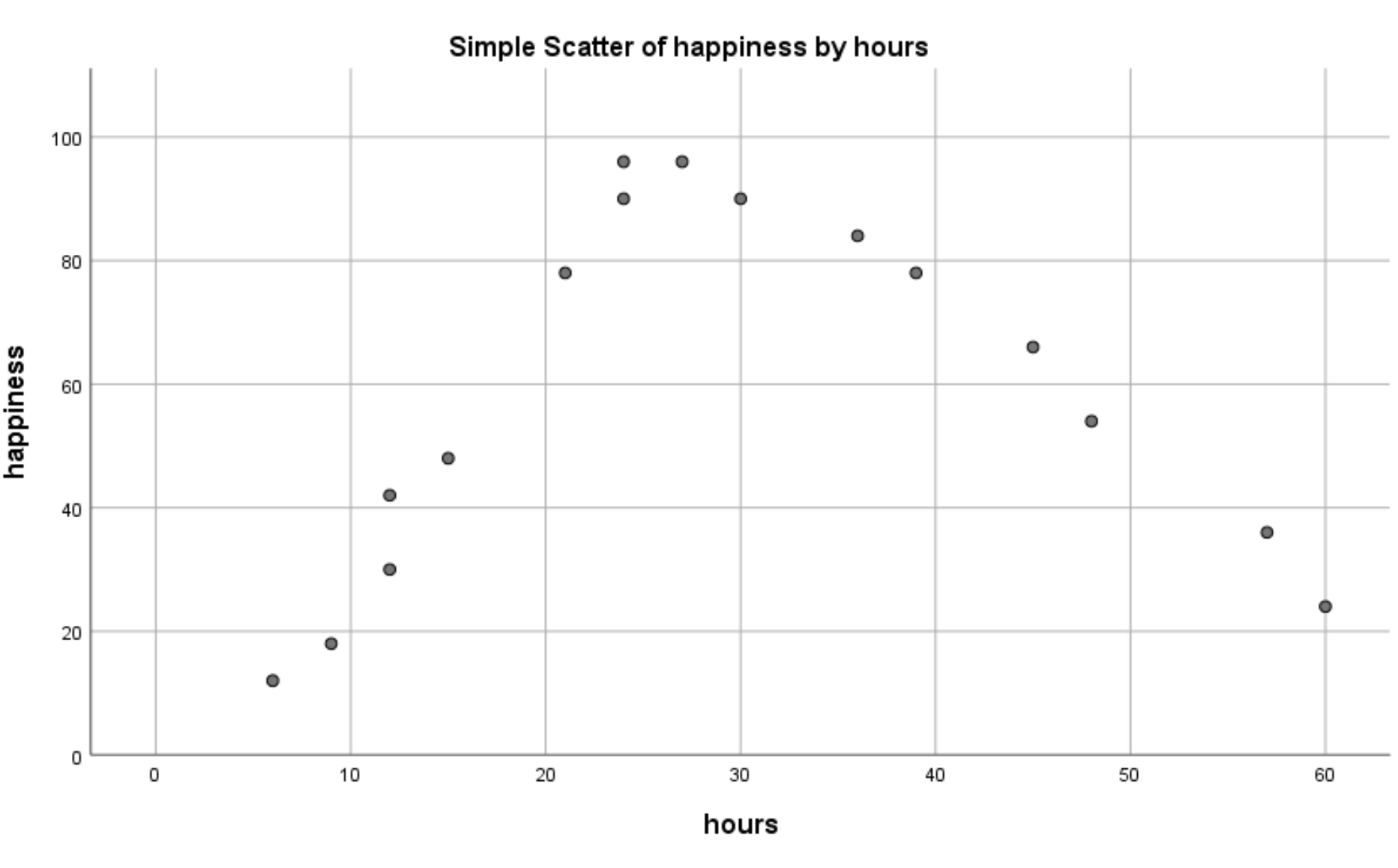
On voit bien qu’il existe une relation non linéaire entre les heures travaillées et le bonheur. Cela nous indique que la régression quadratique est une technique appropriée à utiliser dans cette situation.

Étape 2 : Créez une nouvelle variable.

Avant de pouvoir effectuer une régression quadratique, nous devons créer une variable prédictive pour les heures ² .

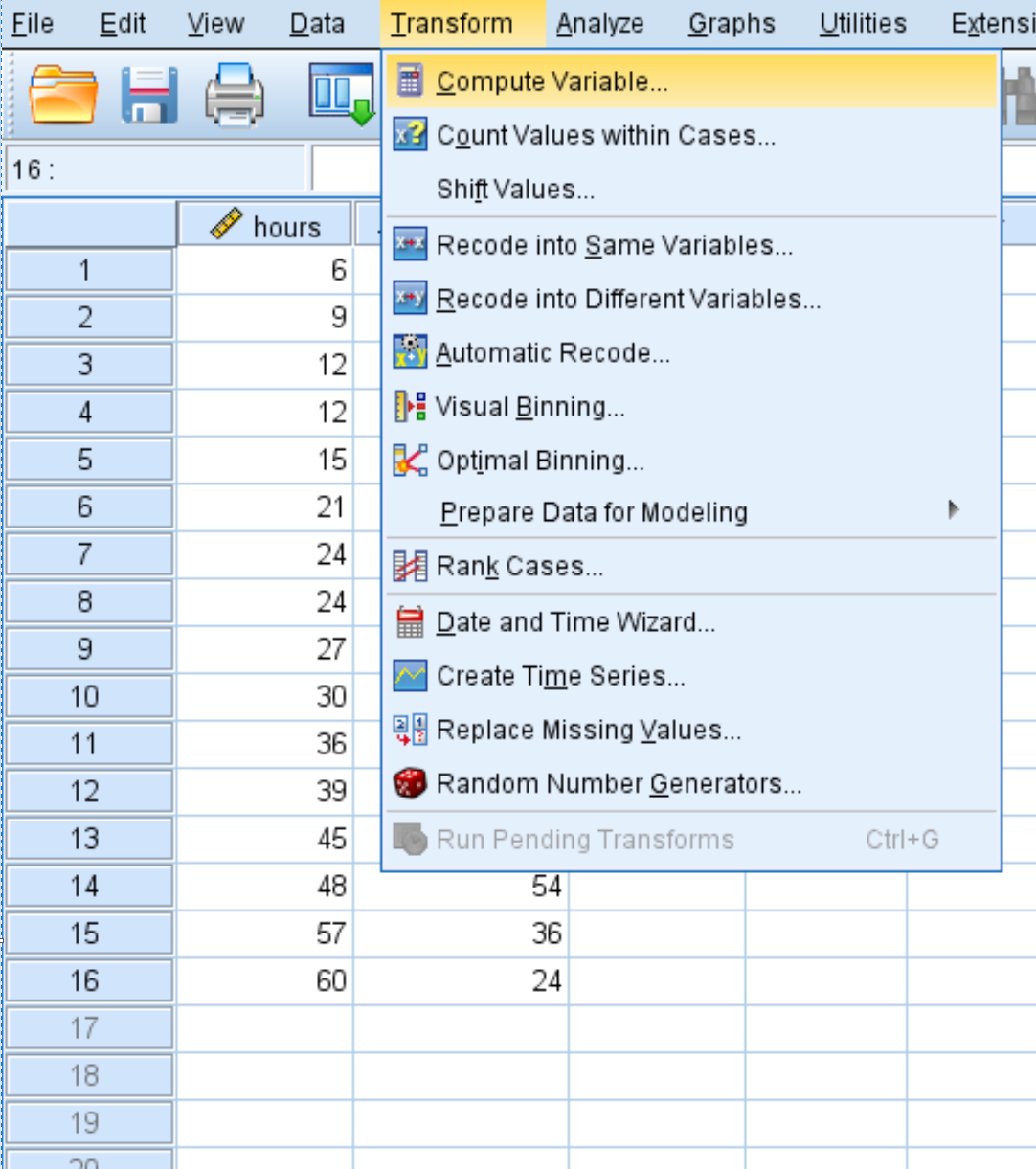
Cliquez sur l’onglet Transformation , puis sur Calculer la variable :

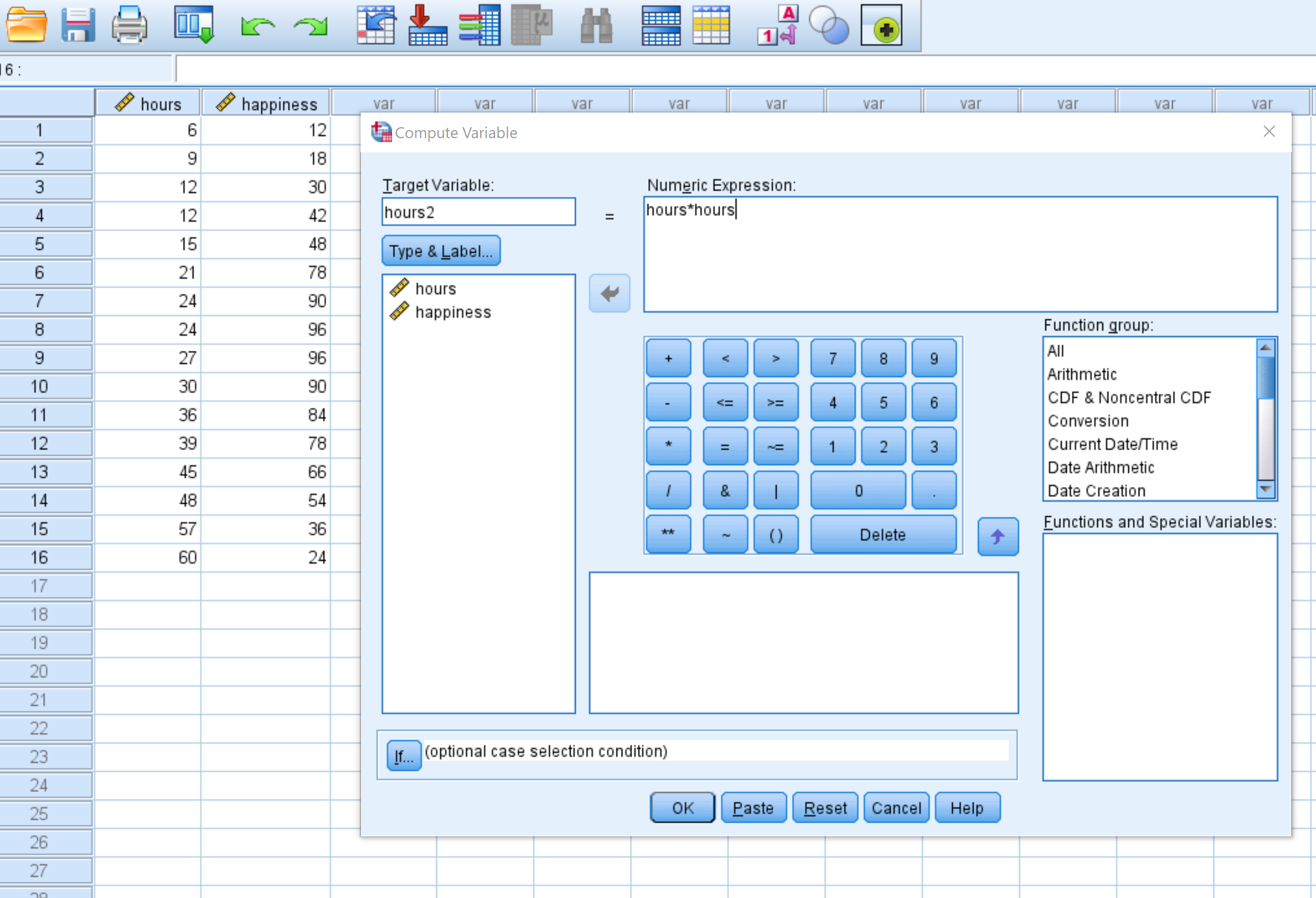
Dans la nouvelle fenêtre qui apparaît, nommez la variable cible hours2 et définissez-la comme hours*hours :

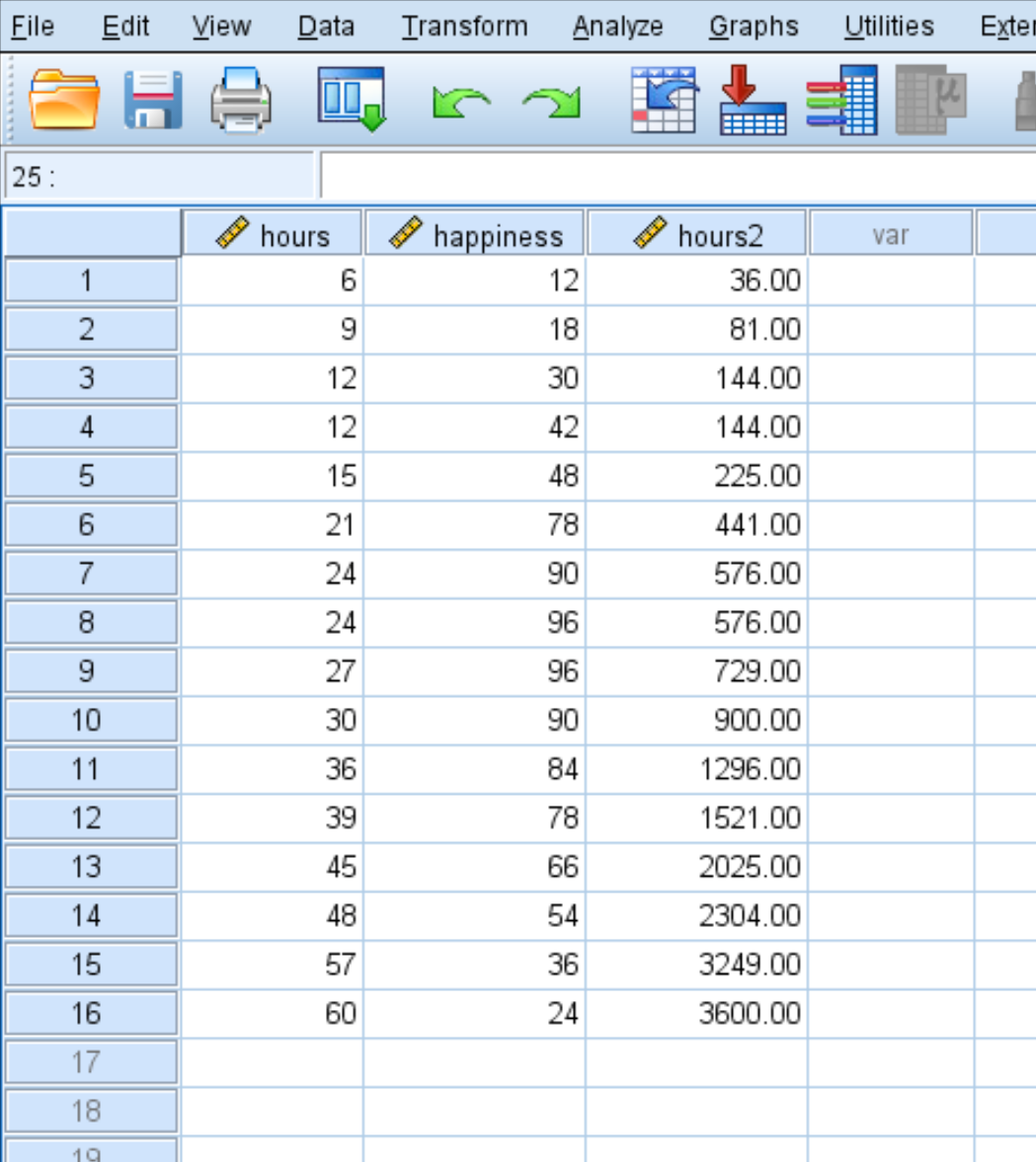
Une fois que vous aurez cliqué sur OK , la variable hours2 apparaîtra dans une nouvelle colonne :

Étape 3 : Effectuez une régression quadratique.

Ensuite, nous effectuerons une régression quadratique. Cliquez sur l’onglet Analyser , puis Régression , puis Linéaire :

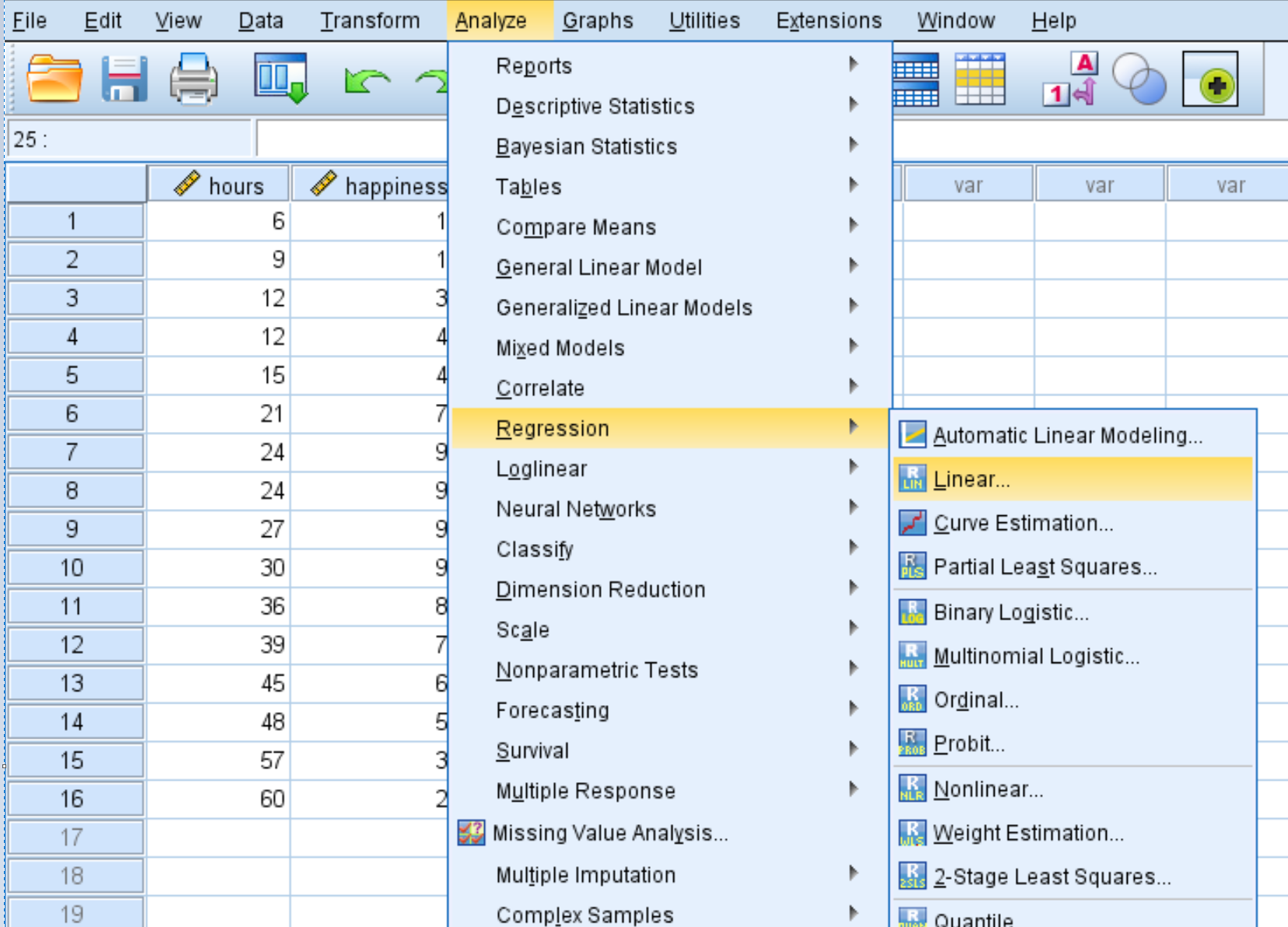
Dans la nouvelle fenêtre qui apparaît, faites glisser le bonheur dans la case intitulée Dépendant. Faites glisser les heures et les heures2 dans la zone intitulée Indépendant(s). Cliquez ensuite sur OK .

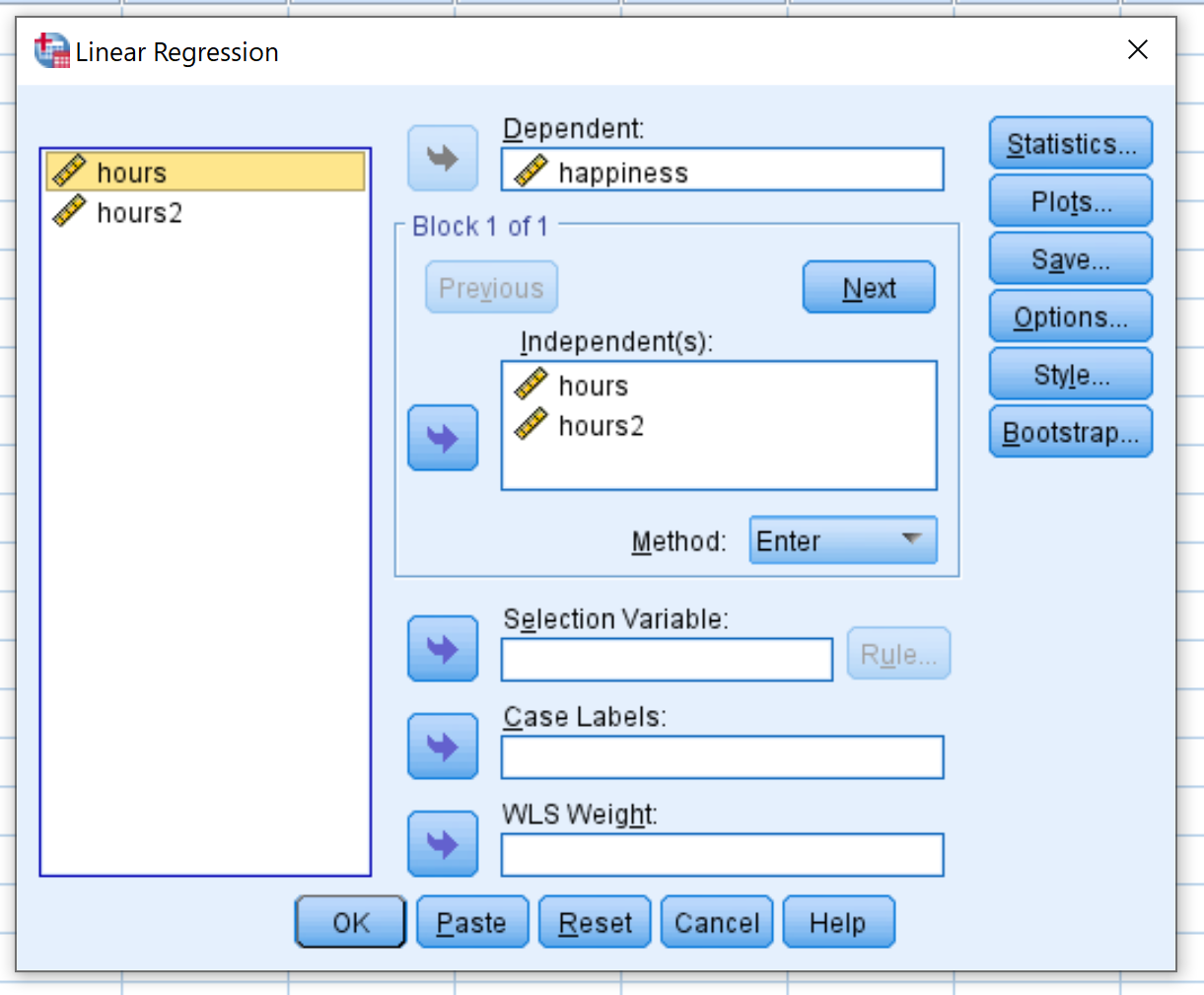
Étape 4 : Interprétez les résultats.

Une fois que vous avez cliqué sur OK , les résultats de la régression quadratique apparaîtront dans une nouvelle fenêtre.

Le premier tableau qui nous intéresse s’intitule Model Summary :

Voici comment interpréter les chiffres les plus pertinents de ce tableau :

• R Carré : Il s’agit de la proportion de la variance de la variable de réponse qui peut être expliquée par les variables explicatives. Dans cet exemple, 90,9 % de la variation du bonheur peut s’expliquer par les variables heures et heures ² .
• Norme. Erreur d’estimation : l’ erreur type est la distance moyenne entre les valeurs observées et la droite de régression. Dans cet exemple, les valeurs observées s’éloignent en moyenne de 9,519 unités de la droite de régression.

Le tableau suivant qui nous intéresse s’intitule ANOVA :

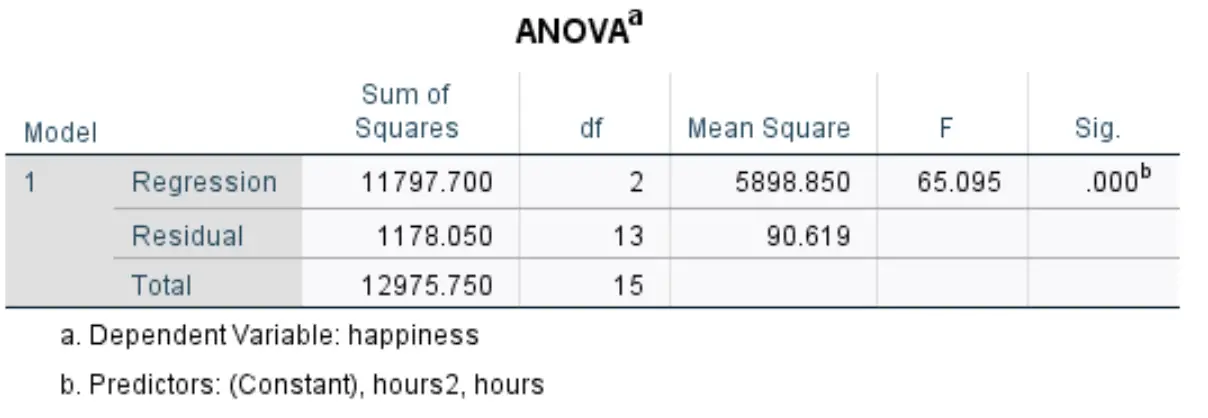
Voici comment interpréter les chiffres les plus pertinents de ce tableau :

• F : Il s’agit de la statistique F globale pour le modèle de régression, calculée comme Régression quadratique moyenne / Résidu quadratique moyen.
• Sig : Il s’agit de la valeur p associée à la statistique F globale. Cela nous indique si le modèle de régression dans son ensemble est statistiquement significatif ou non. Dans ce cas, la valeur p est égale à 0,000, ce qui indique que les variables explicatives heures et heures ² combinées ont une association statistiquement significative avec le résultat de l’examen.

Le tableau suivant qui nous intéresse s’intitule Coefficients :

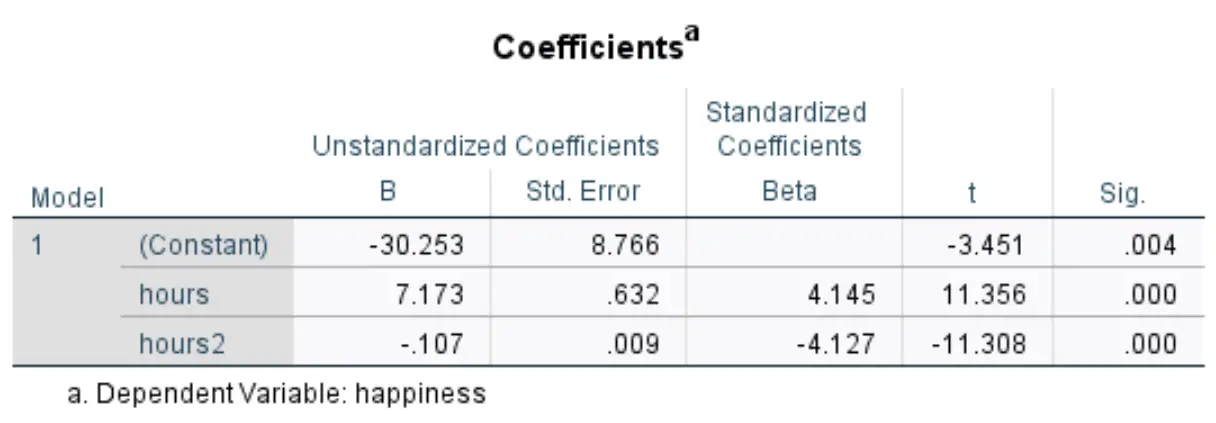
Nous pouvons utiliser les valeurs de la colonne Non standardisé B pour former l’équation de régression estimée pour cet ensemble de données :

Niveau de bonheur estimé = -30,253 + 7,173*(heures) – 0,107*(heures ² )

Nous pouvons utiliser cette équation pour trouver le niveau de bonheur estimé d’un individu en fonction du nombre d’heures travaillées par semaine. Par exemple, une personne qui travaille 60 heures par semaine devrait avoir un niveau de bonheur de 14,97 :

Niveau de bonheur estimé = -30,253 + 7,173*(60) – 0,107*(60 ² ) = 14,97 .

À l’inverse, une personne qui travaille 30 heures par semaine devrait avoir un niveau de bonheur de 88,65 :

Niveau de bonheur estimé = -30,253 + 7,173*(30) – 0,107*(30 ² ) = 88,65 .

Étape 5 : Rapportez les résultats.

Enfin, nous souhaitons rapporter les résultats de notre régression quadratique. Voici un exemple de la façon de procéder :

Une régression quadratique a été réalisée pour quantifier la relation entre le nombre d’heures travaillées par un individu et son niveau de bonheur correspondant (mesuré de 0 à 100). Un échantillon de 16 personnes a été utilisé dans l’analyse.

Les résultats ont montré qu’il existait une relation statistiquement significative entre les variables explicatives heures et heures ² et la variable de réponse bonheur (F(2, 13) = 65,095, p < 0,000).

Ensemble, ces deux variables explicatives représentaient 90,9 % de la variabilité du bonheur.

L’équation de régression s’est avérée être :

Niveau de bonheur estimé = -30,253 + 7,173 (heures) – 0,107 (heures ² )