Comment effectuer une régression quantile en Python

La régression linéaire est une méthode que nous pouvons utiliser pour comprendre la relation entre une ou plusieurs variables prédictives et une variable de réponse .

Généralement, lorsque nous effectuons une régression linéaire, nous souhaitons estimer la valeur moyenne de la variable de réponse.

Cependant, nous pourrions plutôt utiliser une méthode connue sous le nom de régression quantile pour estimer toute valeur quantile ou centile de la valeur de réponse, telle que le 70e centile, le 90e centile, le 98e centile, etc.

Ce didacticiel fournit un exemple étape par étape de la façon d’utiliser cette fonction pour effectuer une régression quantile en Python.

Étape 1 : Chargez les packages nécessaires

Tout d’abord, nous allons charger les packages et fonctions nécessaires :

import numpy as np
import pandas as pd
import statsmodels.api as sm
import statsmodels.formula.api as smf
import matplotlib.pyplot as plt

Étape 2 : Créer les données

Pour cet exemple, nous allons créer un ensemble de données contenant les heures étudiées et les résultats des examens obtenus pour 100 étudiants dans une université :

#make this example reproducible
np.random.seed(0)

#create dataset
obs = 100

hours = np.random.uniform(1, 10, obs)
score = 60 + 2*hours + np.random.normal(loc=0, scale=.45*hours, size=100)

df = pd.DataFrame({'hours': hours, 'score': score})

#view first five rows
df.head()

hours	score
0	5.939322	68.764553
1	7.436704	77.888040
2	6.424870	74.196060
3	5.903949	67.726441
4	4.812893	72.849046

Étape 3 : Effectuer une régression quantile

Ensuite, nous ajusterons un modèle de régression quantile en utilisant les heures étudiées comme variable prédictive et les résultats à l’examen comme variable de réponse.

Nous utiliserons le modèle pour prédire le 90e centile attendu des résultats aux examens en fonction du nombre d’heures étudiées :

#fit the model
model = smf.quantreg('score ~ hours', df).fit(q=0.9)

#view model summary
print(model.summary())

                         QuantReg Regression Results                          
==============================================================================
Dep. Variable:                  score   Pseudo R-squared:               0.6057
Model:                       QuantReg   Bandwidth:                       3.822
Method:                 Least Squares   Sparsity:                        10.85
Date:                Tue, 29 Dec 2020   No. Observations:                  100
Time:                        15:41:44   Df Residuals:                       98
                                        Df Model:                            1
==============================================================================
                 coef    std err          t      P>|t|      [0.025      0.975]
------------------------------------------------------------------------------
Intercept     59.6104      0.748     79.702      0.000      58.126      61.095
hours          2.8495      0.128     22.303      0.000       2.596       3.103
==============================================================================

À partir du résultat, nous pouvons voir l’équation de régression estimée :

90e percentile de la note de l’examen = 59,6104 + 2,8495*(heures)

Par exemple, le 90e percentile des scores de tous les étudiants qui étudient 8 heures devrait être de 82,4 :

90e percentile de la note de l’examen = 59,6104 + 2,8495*(8) = 82,4 .

La sortie affiche également les limites de confiance supérieure et inférieure pour l’interception et les heures de la variable prédictive.

Étape 4 : Visualisez les résultats

Nous pouvons également visualiser les résultats de la régression en créant un nuage de points avec l’équation de régression quantile ajustée superposée sur le graphique :

#define figure and axis
fig, ax = plt.subplots(figsize=(8, 6))

#get y values
get_y = lambda a, b: a + b * hours
y = get_y(model.params['Intercept'], model.params['hours'])

#plot data points with quantile regression equation overlaid
ax.plot(hours, y, color='black')
ax.scatter(hours, score, alpha=.3)
ax.set_xlabel('Hours Studied', fontsize=14)
ax.set_ylabel('Exam Score', fontsize=14)

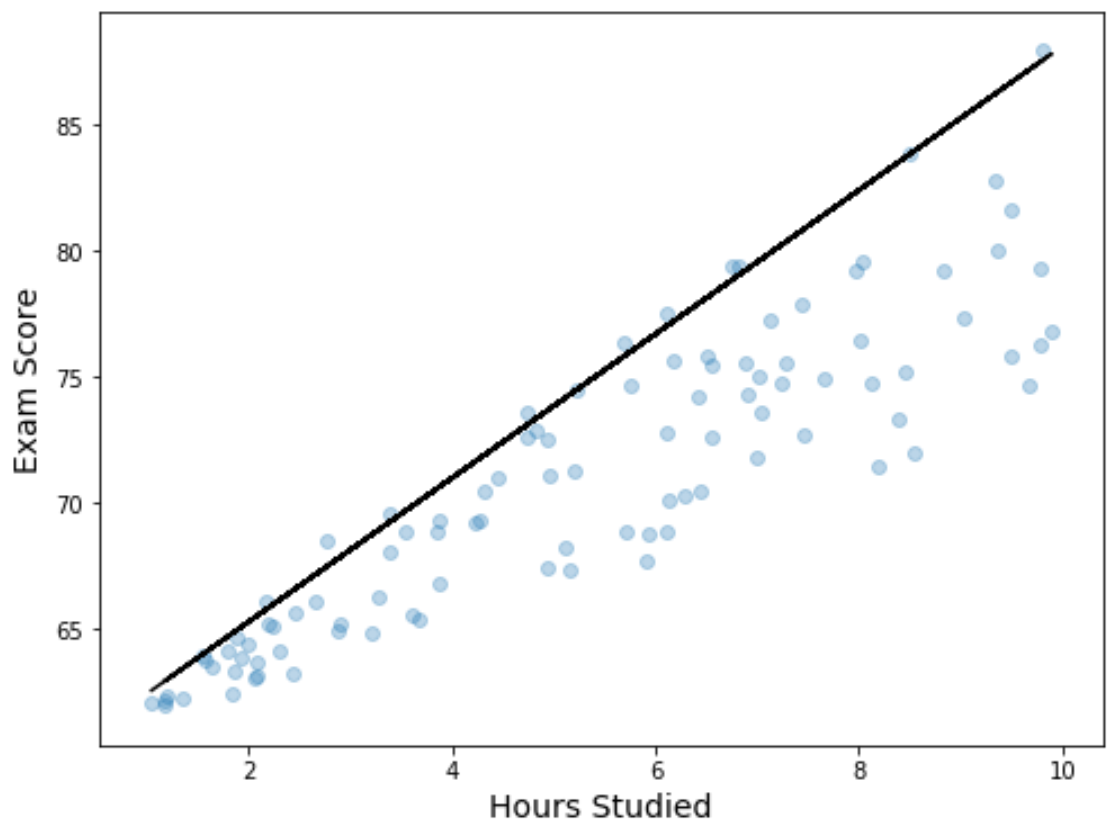
Contrairement à une simple ligne de régression linéaire, notez que cette ligne ajustée ne représente pas la « ligne de meilleur ajustement » pour les données. Au lieu de cela, il passe par le 90e percentile estimé à chaque niveau de la variable prédictive.

Ressources additionnelles

Comment effectuer une régression linéaire simple en Python
Comment effectuer une régression quadratique en Python