Comment effectuer une régression quantile dans R
La régression linéaire est une méthode que nous pouvons utiliser pour comprendre la relation entre une ou plusieurs variables prédictives et une variable de réponse .
Généralement, lorsque nous effectuons une régression linéaire, nous souhaitons estimer la valeur moyenne de la variable de réponse.
Cependant, nous pourrions plutôt utiliser une méthode connue sous le nom de régression quantile pour estimer toute valeur quantile ou centile de la valeur de réponse, telle que le 70e centile, le 90e centile, le 98e centile, etc.
Pour effectuer une régression quantile dans R, nous pouvons utiliser la fonction rq() du package quantreg , qui utilise la syntaxe suivante :
library(quantreg) model <- rq(y ~ x, data = dataset, tau = 0.5)
où:
- y : la variable de réponse
- x : la ou les variables prédictives
- data : le nom de l’ensemble de données
- tau : Le centile à trouver. La valeur par défaut est la médiane (tau = 0,5), mais vous pouvez la définir sur n’importe quel nombre compris entre 0 et 1.
Ce didacticiel fournit un exemple étape par étape de la façon d’utiliser cette fonction pour effectuer une régression quantile dans R.
Étape 1 : Saisissez les données
Pour cet exemple, nous allons créer un ensemble de données contenant les heures étudiées et les résultats des examens obtenus pour 100 étudiants différents dans une université :
#make this example reproducible set.seed(0) #create data frame hours <- runif(100, 1, 10) score <- 60 + 2*hours + rnorm(100, mean=0, sd=.45*hours) df <- data.frame(hours, score) #view first six rows head(df) hours score 1 9.070275 79.22682 2 3.389578 66.20457 3 4.349115 73.47623 4 6.155680 70.10823 5 9.173870 78.12119 6 2.815137 65.94716
Étape 2 : Effectuer une régression quantile
Ensuite, nous ajusterons un modèle de régression quantile en utilisant les heures étudiées comme variable prédictive et les résultats à l’examen comme variable de réponse.
Nous utiliserons le modèle pour prédire le 90e centile attendu des résultats aux examens en fonction du nombre d’heures étudiées :
library(quantreg) #fit model model <- rq(score ~ hours, data = df, tau = 0.9) #view summary of model summary(model) Call: rq(formula = score ~ hours, tau = 0.9, data = df) tau: [1] 0.9 Coefficients: coefficients lower bd upper bd (Intercept) 60.25185 59.27193 62.56459 hours 2.43746 1.98094 2.76989
À partir du résultat, nous pouvons voir l’équation de régression estimée :
90e percentile de la note de l’examen = 60,25 + 2,437*(heures)
Par exemple, le 90e percentile des scores de tous les étudiants qui étudient 8 heures devrait être de 79,75 :
90e percentile de la note de l’examen = 60,25 + 2,437*(8) = 79,75 .
La sortie affiche également les limites de confiance supérieure et inférieure pour l’interception et les heures de la variable prédictive.
Étape 3 : Visualisez les résultats
Nous pouvons également visualiser les résultats de la régression en créant un nuage de points avec l’équation de régression quantile ajustée superposée sur le graphique :
library(ggplot2) #create scatterplot with quantile regression line ggplot(df, aes(hours,score)) + geom_point() + geom_abline(intercept=coef(model)[1], slope=coef(model)[2])
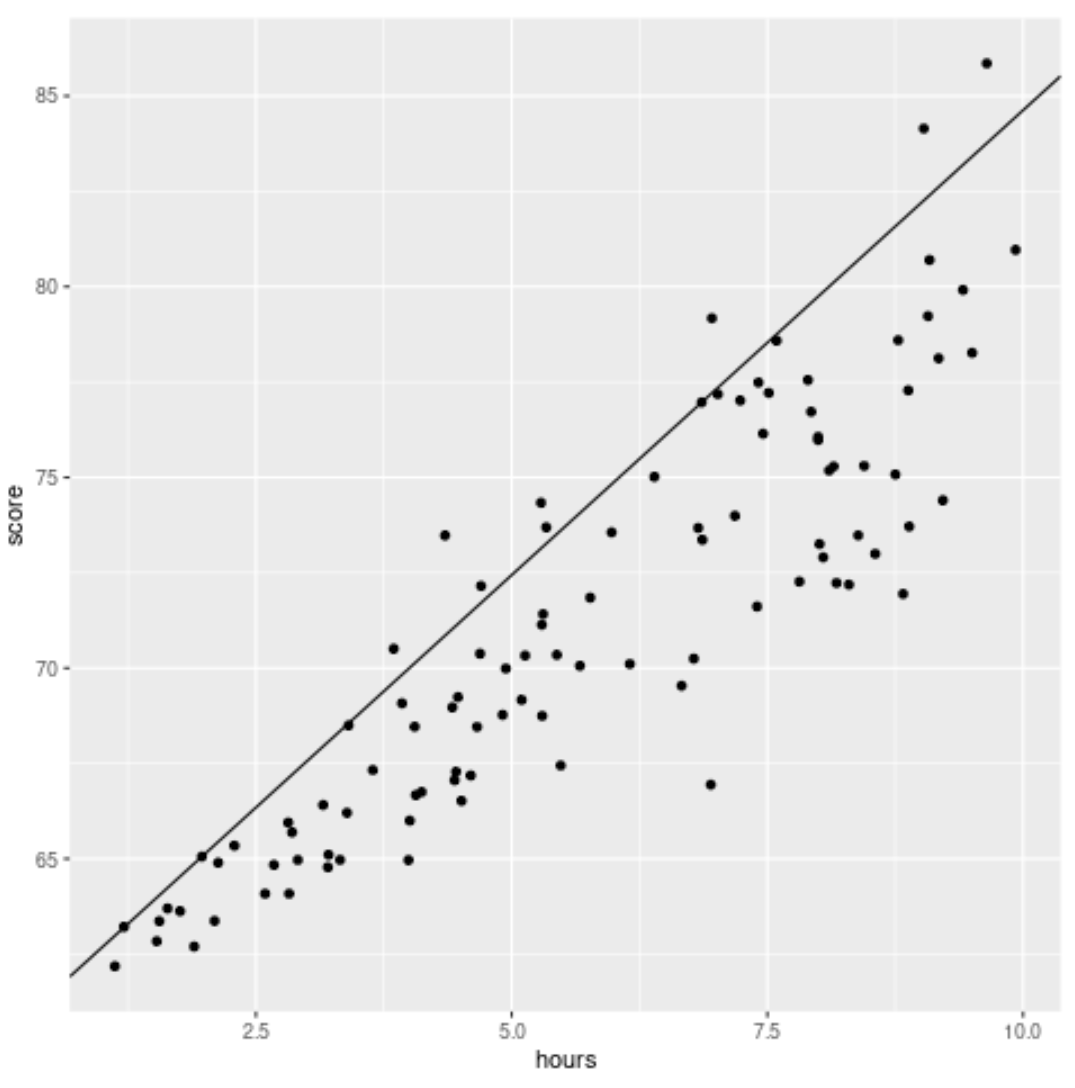
Contrairement à une droite de régression linéaire traditionnelle, notez que cette droite ajustée ne traverse pas le cœur des données. Au lieu de cela, il passe par le 90e percentile estimé à chaque niveau de la variable prédictive.
Nous pouvons voir la différence entre l’équation de régression quantile ajustée et l’équation de régression linéaire simple en ajoutant l’argument geom_smooth() :
library(ggplot2) #create scatterplot with quantile regression line and simple linear regression line ggplot(df, aes(hours,score)) + geom_point() + geom_abline(intercept=coef(model)[1], slope=coef(model)[2]) + geom_smooth(method="lm", se=F)
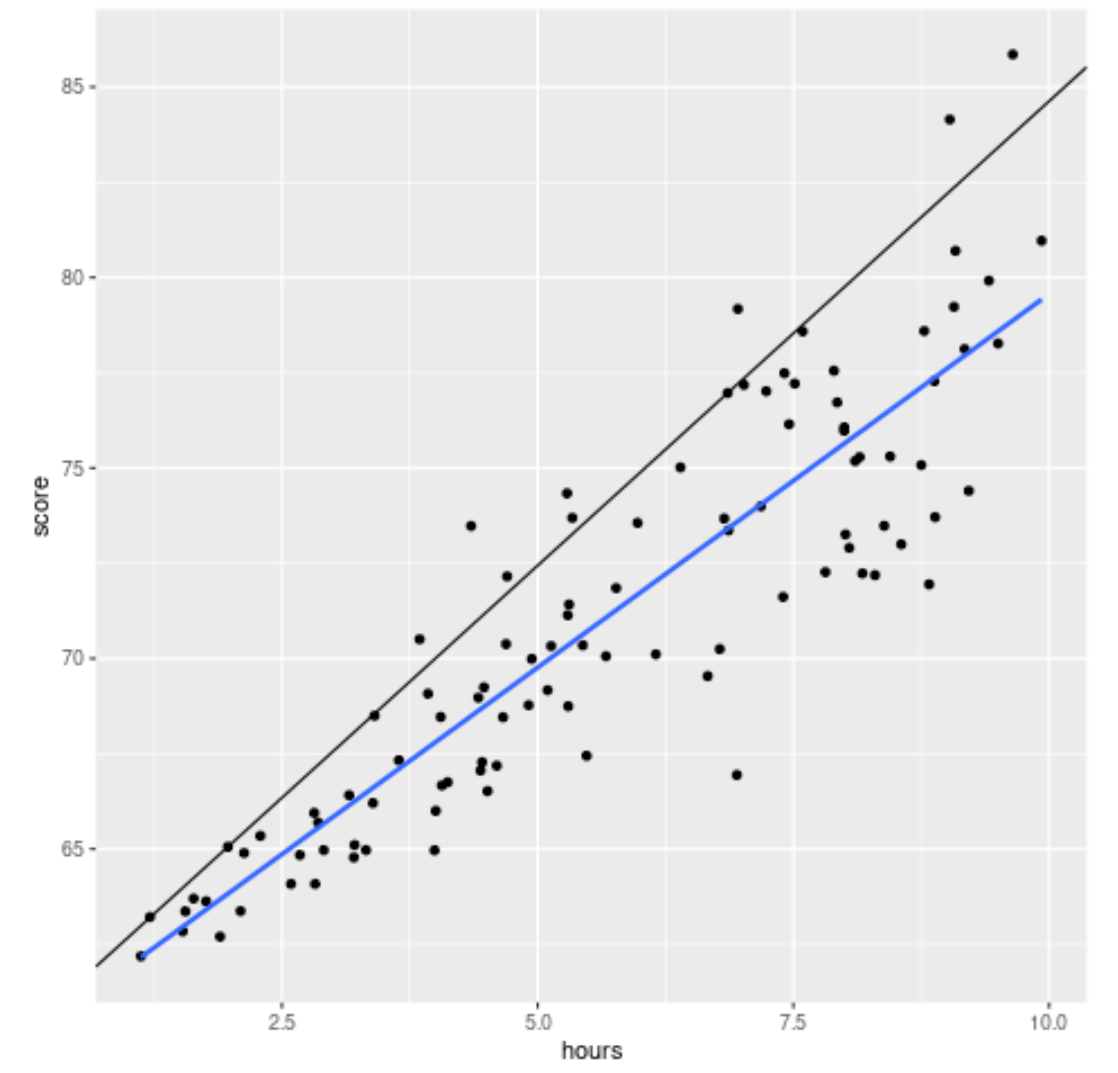
La ligne noire affiche la ligne de régression quantile ajustée pour le 90e centile et la ligne bleue affiche la ligne de régression linéaire simple, qui estime la valeur moyenne de la variable de réponse.
Comme prévu, la simple ligne de régression linéaire traverse les données et nous montre la valeur moyenne estimée des résultats aux examens à chaque niveau d’heures.
Ressources additionnelles
Les didacticiels suivants expliquent comment effectuer d’autres tâches courantes dans R :
Comment effectuer une régression linéaire simple dans R
Comment effectuer une régression linéaire multiple dans R
Comment effectuer une régression quadratique dans R
