Comment effectuer une régression robuste dans R (étape par étape)

La régression robuste est une méthode que nous pouvons utiliser comme alternative à la régression des moindres carrés ordinaire lorsqu’il existe des valeurs aberrantes ou des observations influentes dans l’ensemble de données avec lequel nous travaillons.

Pour effectuer une régression robuste dans R, nous pouvons utiliser la fonction rlm() du package MASS , qui utilise la syntaxe suivante :

L’exemple étape par étape suivant montre comment effectuer une régression robuste dans R pour un ensemble de données donné.

Étape 1 : Créer les données

Tout d’abord, créons un faux ensemble de données avec lequel travailler :

#create data
df <- data.frame(x1=c(1, 3, 3, 4, 4, 6, 6, 8, 9, 3,
                      11, 16, 16, 18, 19, 20, 23, 23, 24, 25),
                 x2=c(7, 7, 4, 29, 13, 34, 17, 19, 20, 12,
                      25, 26, 26, 26, 27, 29, 30, 31, 31, 32),
                  y=c(17, 170, 19, 194, 24, 2, 25, 29, 30, 32,
                      44, 60, 61, 63, 63, 64, 61, 67, 59, 70))

#view first six rows of data
head(df)

  x1 x2   y
1  1  7  17
2  3  7 170
3  3  4  19
4  4 29 194
5  4 13  24
6  6 34   2

Étape 2 : Effectuer une régression des moindres carrés ordinaires

Ajustons ensuite un modèle de régression des moindres carrés ordinaire et créons un tracé des résidus standardisés .

En pratique, on considère souvent tout résidu standardisé dont la valeur absolue est supérieure à 3 comme une valeur aberrante.

#fit ordinary least squares regression model
ols <- lm(y~x1+x2, data=df)

#create plot of y-values vs. standardized residuals
plot(df$y, rstandard(ols), ylab='Standardized Residuals', xlab='y') 
abline(h=0)

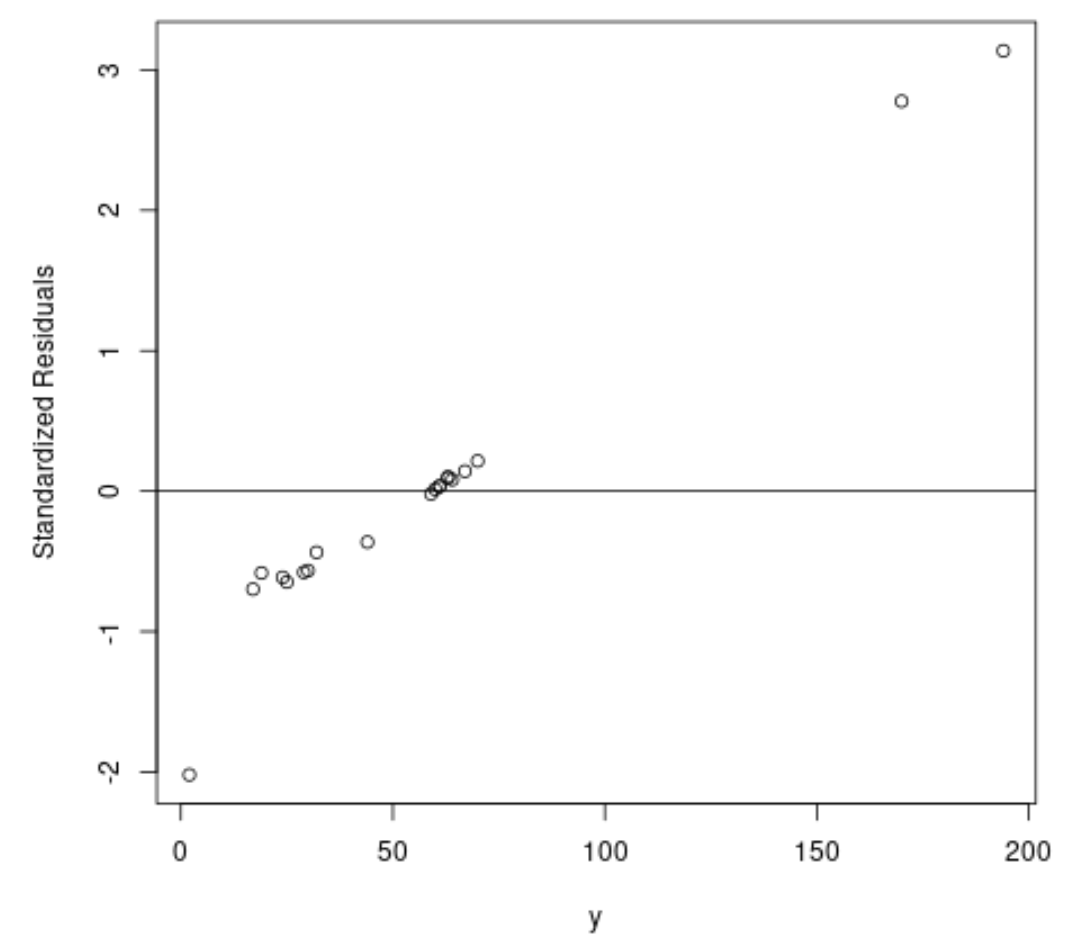
Sur le graphique, nous pouvons voir qu’il existe deux observations avec des résidus standardisés autour de 3.

Cela indique qu’il existe deux valeurs aberrantes potentielles dans l’ensemble de données et que nous pourrions donc bénéficier d’une régression robuste à la place.

Étape 3 : Effectuer une régression robuste

Utilisons ensuite la fonction rlm() pour ajuster un modèle de régression robuste :

library(MASS)

#fit robust regression model
robust <- rlm(y~x1+x2, data=df)

Pour déterminer si ce modèle de régression robuste offre un meilleur ajustement aux données par rapport au modèle OLS, nous pouvons calculer l’erreur type résiduelle de chaque modèle.

L’erreur type résiduelle (RSE) est un moyen de mesurer l’écart type des résidus dans un modèle de régression. Plus la valeur du RSE est faible, plus un modèle est capable de s’adapter aux données.

Le code suivant montre comment calculer le RSE pour chaque modèle :

#find residual standard error of ols model
summary(ols)$sigma

[1] 49.41848

#find residual standard error of ols model
summary(robust)$sigma

[1] 9.369349

Nous pouvons voir que le RSE du modèle de régression robuste est bien inférieur à celui du modèle de régression des moindres carrés ordinaire, ce qui nous indique que le modèle de régression robuste offre un meilleur ajustement aux données.

Ressources additionnelles

Comment effectuer une régression linéaire simple dans R
Comment effectuer une régression linéaire multiple dans R
Comment effectuer une régression polynomiale dans R