Comment effectuer une régression spline dans R (avec exemple)

La régression spline est un type de régression utilisé lorsqu’il existe des points ou des « nœuds » où le modèle dans les données change brusquement et où la régression linéaire et la régression polynomiale ne sont pas suffisamment flexibles pour s’adapter aux données.

L’exemple suivant, étape par étape, montre comment effectuer une régression spline dans R.

Étape 1 : Créer les données

Tout d’abord, créons un ensemble de données dans R avec deux variables et créons un nuage de points pour visualiser la relation entre les variables :

#create data frame
df <- data.frame(x=1:20,
                 y=c(2, 4, 7, 9, 13, 15, 19, 16, 13, 10,
                     11, 14, 15, 15, 16, 15, 17, 19, 18, 20))

#view head of data frame
head(df)

  x  y
1 1  2
2 2  4
3 3  7
4 4  9
5 5 13
6 6 15

#create scatterplot
plot(df$x, df$y, cex=1.5, pch=19)

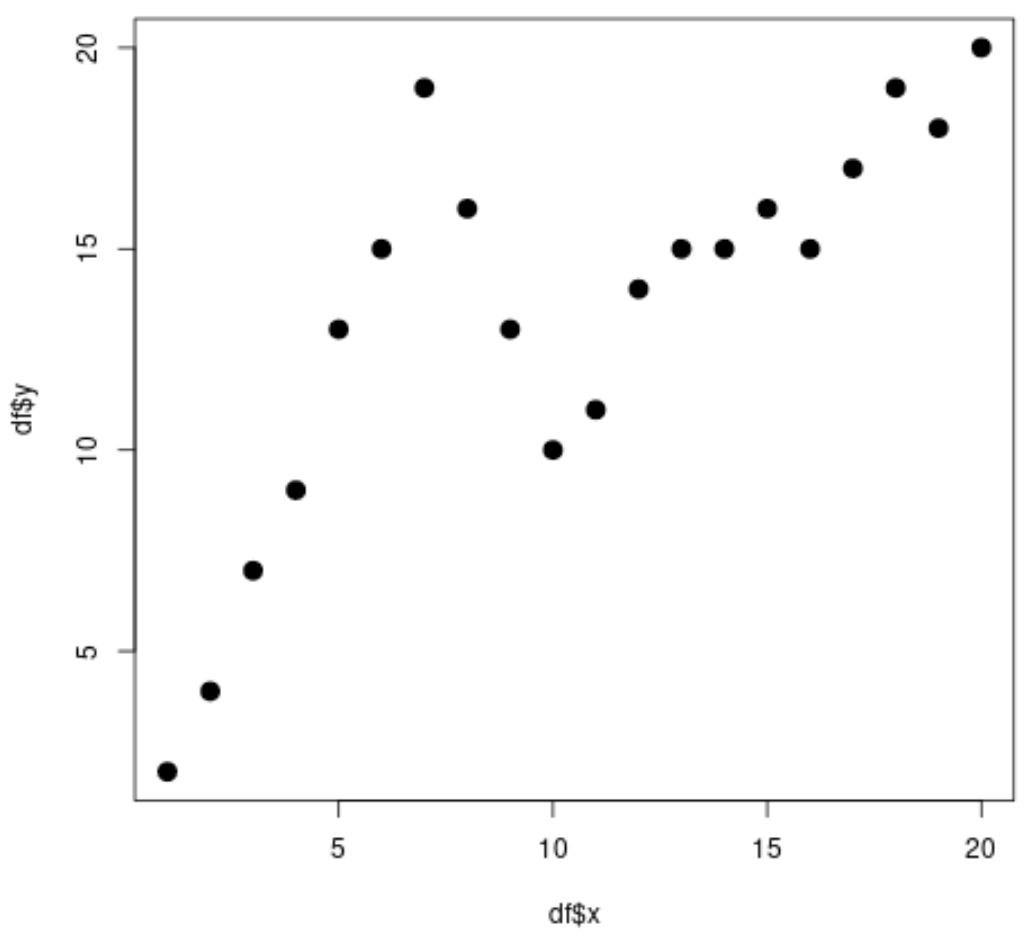
De toute évidence, la relation entre x et y est non linéaire et il semble y avoir deux points ou « nœuds » où le modèle dans les données change brusquement à x = 7 et x = 10.

Étape 2 : Ajuster le modèle de régression linéaire simple

Utilisons ensuite la fonction lm() pour ajuster un modèle de régression linéaire simple à cet ensemble de données et traçons la droite de régression ajustée sur le nuage de points :

#fit simple linear regression model
linear_fit <- lm(df$y ~ df$x)

#view model summary
summary(linear_fit)

Call:
lm(formula = df$y ~ df$x)

Residuals:
    Min      1Q  Median      3Q     Max 
-5.2143 -1.6327 -0.3534  0.6117  7.8789 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)   6.5632     1.4643   4.482 0.000288 ***
df$x          0.6511     0.1222   5.327  4.6e-05 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.152 on 18 degrees of freedom
Multiple R-squared:  0.6118,	Adjusted R-squared:  0.5903 
F-statistic: 28.37 on 1 and 18 DF,  p-value: 4.603e-05

#create scatterplot
plot(df$x, df$y, cex=1.5, pch=19)

#add regression line to scatterplot
abline(linear_fit)

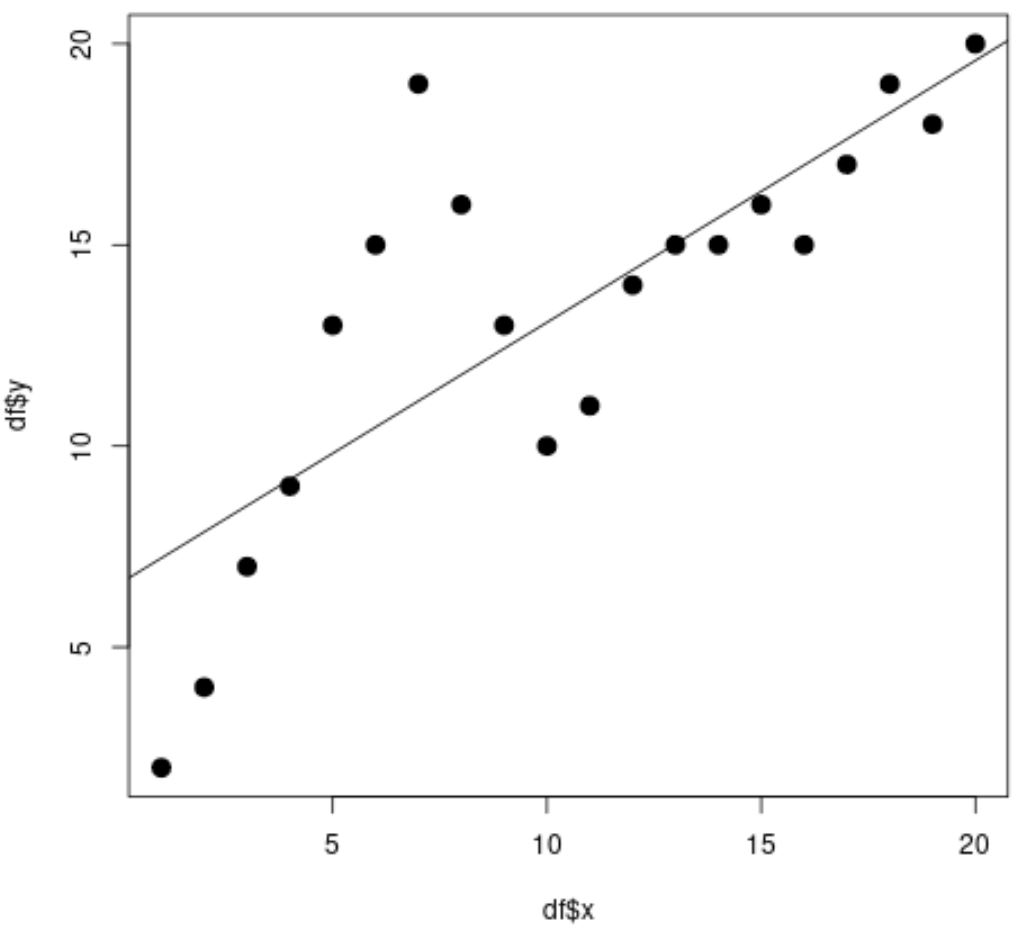
À partir du nuage de points, nous pouvons voir que la simple ligne de régression linéaire ne correspond pas bien aux données.

À partir des résultats du modèle, nous pouvons également voir que la valeur R-carré ajustée est de 0,5903 .

Nous comparerons cela à la valeur R-carré ajustée d’un modèle spline.

Étape 3 : Ajuster le modèle de régression spline

Utilisons ensuite la fonction bs() du package splines pour ajuster un modèle de régression spline avec deux nœuds, puis traçons le modèle ajusté sur le nuage de points :

library(splines)

#fit spline regression model
spline_fit <- lm(df$y ~ bs(df$x, knots=c(7, 10)))

#view summary of spline regression model
summary(spline_fit)

Call:
lm(formula = df$y ~ bs(df$x, knots = c(7, 10)))

Residuals:
     Min       1Q   Median       3Q      Max 
-2.84883 -0.94928  0.08675  0.78069  2.61073 

Coefficients:
                            Estimate Std. Error t value Pr(>|t|)    
(Intercept)                    2.073      1.451   1.429    0.175    
bs(df$x, knots = c(7, 10))1    2.173      3.247   0.669    0.514    
bs(df$x, knots = c(7, 10))2   19.737      2.205   8.949 3.63e-07 ***
bs(df$x, knots = c(7, 10))3    3.256      2.861   1.138    0.274    
bs(df$x, knots = c(7, 10))4   19.157      2.690   7.121 5.16e-06 ***
bs(df$x, knots = c(7, 10))5   16.771      1.999   8.391 7.83e-07 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.568 on 14 degrees of freedom
Multiple R-squared:  0.9253,	Adjusted R-squared:  0.8987 
F-statistic:  34.7 on 5 and 14 DF,  p-value: 2.081e-07

#calculate predictions using spline regression model
x_lim <- range(df$x)
x_grid <- seq(x_lim[1], x_lim[2])
preds <- predict(spline_fit, newdata=list(x=x_grid))

#create scatter plot with spline regression predictions
plot(df$x, df$y, cex=1.5, pch=19)
lines(x_grid, preds)

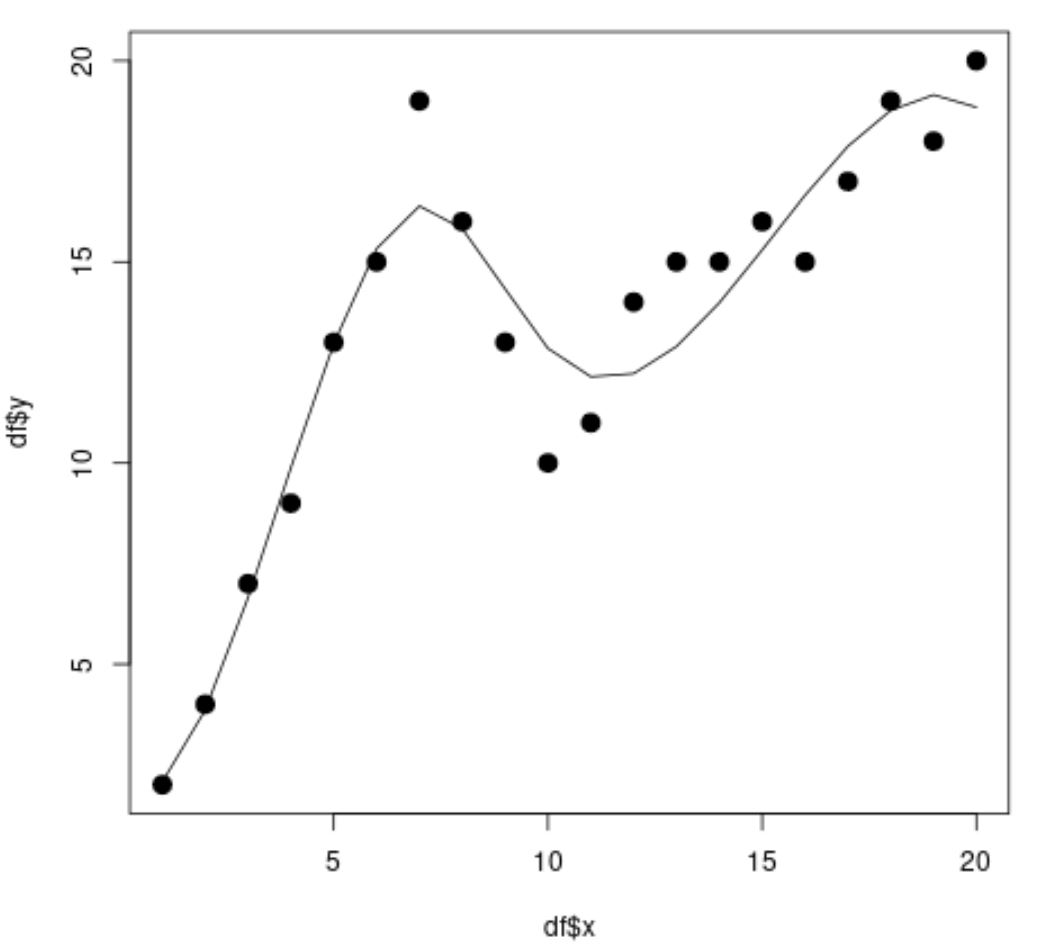
À partir du nuage de points, nous pouvons voir que le modèle de régression spline est capable de s’adapter assez bien aux données.

À partir des résultats du modèle, nous pouvons également voir que la valeur R-carré ajustée est de 0,8987 .

La valeur R au carré ajustée pour ce modèle est beaucoup plus élevée que le modèle de régression linéaire simple, ce qui nous indique que le modèle de régression spline est capable de mieux ajuster les données.

Notez que pour cet exemple nous avons choisi que les nœuds soient situés à x=7 et x=10.

En pratique, vous devrez choisir vous-même l’emplacement des nœuds en fonction de l’endroit où les modèles dans les données semblent changer et en fonction de votre expertise dans le domaine.

Ressources additionnelles

Les didacticiels suivants expliquent comment effectuer d’autres tâches courantes dans R :

Comment effectuer une régression linéaire multiple dans R
Comment effectuer une régression exponentielle dans R
Comment effectuer une régression des moindres carrés pondérés dans R