La relation entre la moyenne & Écart type (avec exemple)
La moyenne représente la valeur moyenne dans un ensemble de données.
Il est calculé comme suit :
Moyenne de l’échantillon = Σx i / n
où:
- Σ : Un symbole qui signifie « somme »
- x i : La i ème observation dans un ensemble de données
- n : le nombre total d’observations dans l’ensemble de données
L’ écart type représente la répartition des valeurs dans un ensemble de données par rapport à la moyenne.
Il est calculé comme suit :
Écart type de l’échantillon = √ Σ(x i – x bar ) 2 / (n-1)
où:
- Σ : Un symbole qui signifie « somme »
- x i : la ième valeur de l’échantillon
- x bar : La moyenne de l’échantillon
- n : La taille de l’échantillon
Notez la relation entre la moyenne et l’écart type : la moyenne est utilisée dans la formule pour calculer l’écart type .
En fait, nous ne pouvons pas calculer l’écart type d’un échantillon à moins de connaître la moyenne de l’échantillon.
L’exemple suivant montre comment calculer la moyenne de l’échantillon et l’écart type de l’échantillon pour un ensemble de données dans la pratique.
Exemple : Calcul de la moyenne et de l’écart type pour un ensemble de données
Supposons que nous ayons l’ensemble de données suivant qui montre les points marqués par 10 joueurs de basket différents :
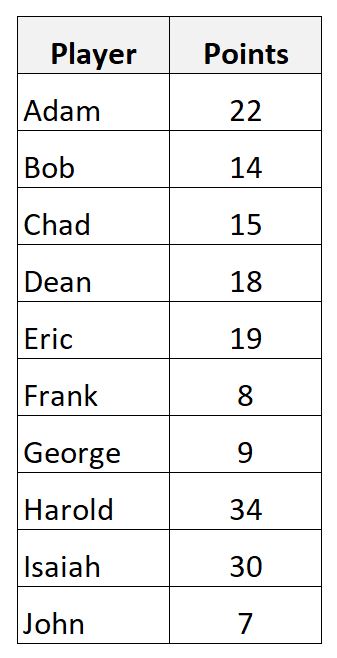Nous pouvons calculer la moyenne de l’échantillon des points marqués en utilisant la formule suivante :
- Moyenne de l’échantillon = Σx i / n
- Moyenne de l’échantillon = (22+14+15+18+19+8+9+34+30+7) / 10
- Moyenne de l’échantillon = 17,6
La moyenne de l’échantillon des points marqués est de 17,6 . Cela représente le nombre moyen de points marqués parmi tous les joueurs.
Une fois que nous connaissons la moyenne de l’échantillon, nous pouvons l’insérer dans la formule pour calculer l’écart type de l’échantillon :
- Écart type de l’échantillon = √ Σ(x i – x bar ) 2 / (n-1)
- Écart type de l’échantillon = √ ((22-17,6) 2 + (14-17,6) 2 + (15-17,6) 2 + (18-17,6) 2 + (19-17,6) 2 + (8-17,6) 2 + (9 -17,6) 2 + (34-17,6) 2 + (30-17,6) 2 + (7-17,6) 2 ) / (10-1)
- Écart type de l’échantillon = 9,08
L’écart type de l’échantillon est de 9,08 . Cela représente la distance moyenne entre chaque valeur de points et la moyenne des points de l’échantillon.
Il est utile de connaître à la fois la moyenne et l’écart type d’un ensemble de données, car chaque métrique nous dit quelque chose de différent.
La moyenne nous donne une idée de l’endroit où se situe la valeur « centrale » d’un ensemble de données.
L’ écart type nous donne une idée de la répartition des valeurs autour de la moyenne dans un ensemble de données. Plus la valeur de l’écart type est élevée, plus les valeurs sont dispersées dans un échantillon.
En connaissant ces deux valeurs, nous pouvons en savoir beaucoup sur la distribution des valeurs dans un ensemble de données.
Ressources additionnelles
Les didacticiels suivants fournissent des informations supplémentaires sur la moyenne et l’écart type :
Pourquoi la moyenne est-elle importante en statistiques ?
Pourquoi l’écart type est-il important dans les statistiques ?
Comment calculer la moyenne et l’écart type dans Excel
à propos de l'auteur
Dr. Benjamin Anderson
Il est un professeur de statistiques à la retraite devenu éducateur dévoué sur Statorials. Avec une vaste expérience et une expertise dans le domaine des statistiques, je m'engage à partager mes connaissances pour responsabiliser les étudiants grâce à Statorials. Lire plus