Répartition des fréquences

Cet article explique ce que sont les distributions de fréquences et comment elles sont réalisées. Vous trouverez également des exemples étape par étape de distributions de fréquences et, en plus, vous pourrez vous entraîner avec des exercices résolus.

Qu’est-ce qu’une distribution de fréquence ?

En statistiques, la distribution de fréquence est un tableau dans lequel les différentes valeurs d’un échantillon sont regroupées en lignes et dans chaque colonne un type de fréquence de chaque valeur est affiché. Par conséquent, la distribution de fréquences sert à montrer tous les types de fréquences dans un ensemble de données.

Plus précisément, une distribution de fréquence comprend une fréquence absolue, une fréquence absolue cumulée, une fréquence relative et une fréquence relative cumulée.

L’une des caractéristiques des distributions de fréquence est qu’elles sont très utiles pour résumer un échantillon statistique d’une variable quantitative et d’une variable qualitative.

Comment faire une distribution de fréquence

Pour réaliser une distribution de fréquence, vous devez suivre les étapes suivantes :

1. Organisez les données en différentes catégories et créez un tableau dans lequel chaque ligne correspond à une catégorie.
2. Calculez la fréquence absolue de chaque catégorie dans la deuxième colonne du tableau.
3. Calculez la fréquence absolue cumulée de chaque catégorie dans la troisième colonne du tableau.
4. Calculez la fréquence relative de chaque catégorie dans la quatrième colonne du tableau.
5. Calculez la fréquence relative cumulée de chaque catégorie dans la cinquième colonne du tableau.
6. En option, deux colonnes peuvent être ajoutées dans lesquelles la fréquence relative et la fréquence relative cumulée sont calculées en pourcentage, pour cela il vous suffit de multiplier les deux colonnes par 100.

Exemple de distribution de fréquence

Une fois que nous avons vu la définition de la distribution de fréquence et la théorie sur la façon dont elle est construite, dans cette section, un exemple est résolu étape par étape.

• Les notes obtenues dans la matière statistique dans une classe de 30 étudiants sont les suivantes. Construisez une distribution de fréquence de l’ensemble de données.

Puisque tous les nombres ne peuvent être que des entiers, il s’agit d’une variable discrète. Il n’est donc pas nécessaire de regrouper les données en intervalles.

Donc, pour faire une distribution de fréquence, nous devons construire un tableau dans lequel chaque valeur différente sera une ligne, puis nous devons trouver la fréquence absolue de chaque valeur :

Notez que la somme de toutes les fréquences absolues équivaut au nombre total de données. Si cette règle n’est pas respectée, cela signifie que vous avez oublié de renseigner certaines informations.

Maintenant que nous connaissons la fréquence absolue, nous devons calculer la fréquence absolue cumulée. Pour ce calcul nous avons deux options : soit on additionne la fréquence absolue de la valeur plus toutes les fréquences absolues des plus petites valeurs, soit au contraire, on additionne la fréquence absolue de la valeur plus la fréquence absolue cumulée de la valeur précédente .

La fréquence absolue cumulée de la dernière valeur correspond toujours au nombre total de données, vous pouvez utiliser cette astuce pour vérifier que les calculs sont corrects.

Ensuite, nous devons déterminer la fréquence relative, qui est calculée en divisant la fréquence absolue par le nombre total de données (30) :

Gardez à l’esprit que la somme de toutes les fréquences relatives est toujours égale à 1, sinon cela signifie qu’un certain calcul de la distribution des fréquences est erroné.

Finalement, il suffit d’extraire la fréquence relative cumulée. Pour ce faire, il faut additionner la fréquence relative de la valeur en question plus toutes les fréquences relatives précédentes ou, ce qui revient au même, la fréquence relative accumulée précédente :

En bref, la distribution de fréquences avec toutes les fréquences des données problématiques est la suivante :

Distribution de fréquence pour les données groupées

Pour faire une distribution de fréquence pour des données regroupées en intervalles , la seule différence est que l’ensemble de données doit d’abord être regroupé en différents intervalles, mais le reste des calculs se fait de la même manière que dans une distribution de fréquence sans regrouper les données.

A titre d’exemple, un problème de construction d’une distribution de fréquence pour des données groupées est résolu ci-dessous.

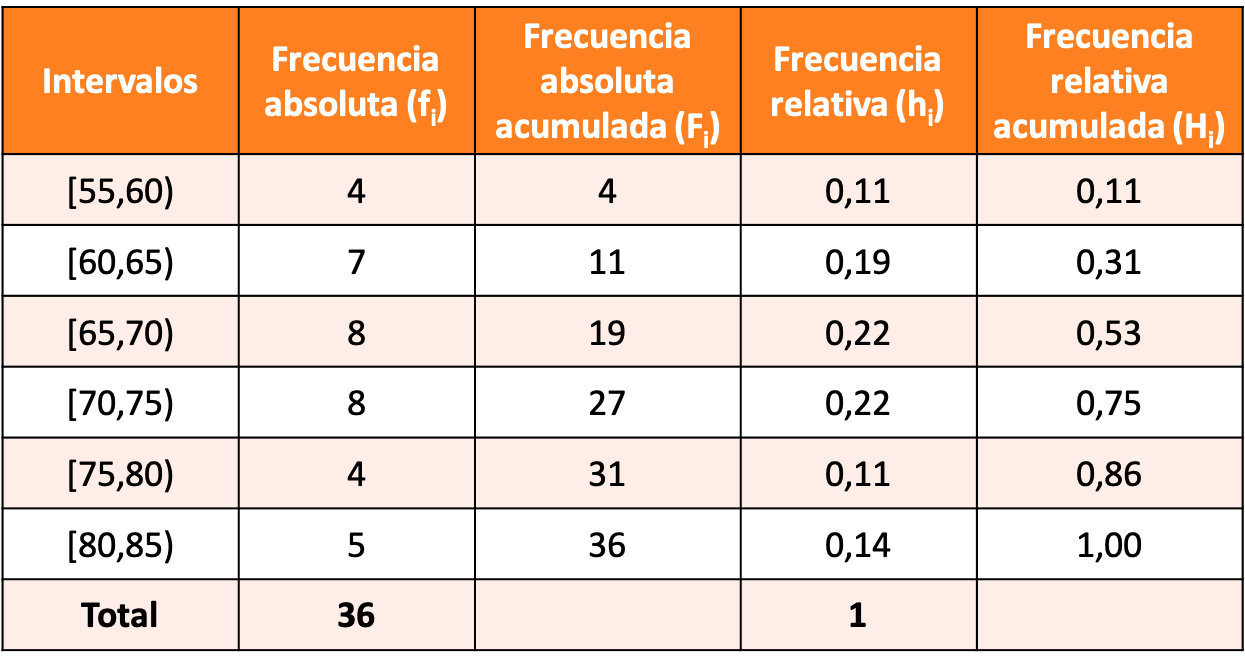
• La taille de 20 personnes a été mesurée et les résultats notés ci-dessous ont été obtenus. Créez une distribution de fréquence en séparant les données en intervalles.

Les données de cet échantillon suivent une distribution continue, puisque les nombres peuvent être décimaux et peuvent donc prendre n’importe quelle valeur. Par conséquent, nous ferons la distribution de fréquence regroupant les données en intervalles.

Bien qu’il existe plusieurs règles mathématiques pour créer les intervalles d’un échantillon, dans ce cas nous créerons simplement des intervalles d’une largeur de 10 dixièmes.

Ainsi, après avoir calculé tous les types de fréquences pour chaque intervalle (la procédure est la même que dans l’exemple ci-dessus), la répartition des fréquences avec les données regroupées en intervalles est la suivante :

Exercices résolus de distributions de fréquences

Exercice 1

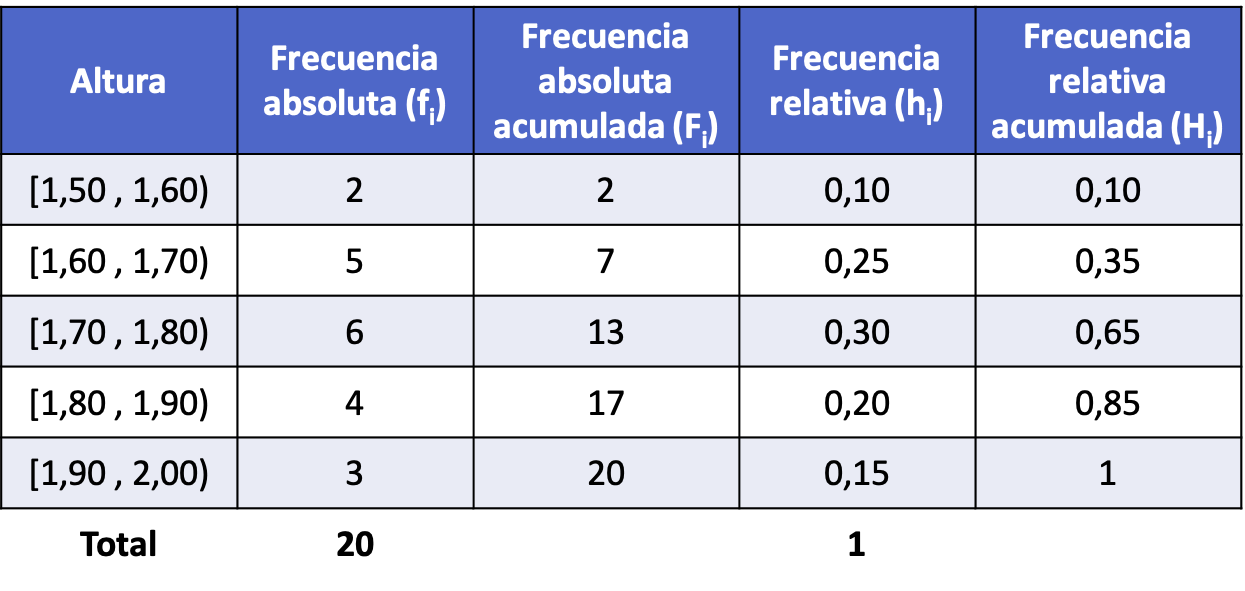
On a demandé à 20 personnes combien de fois elles vont au cinéma par mois et voici les résultats :

Faites une distribution de fréquence avec l’échantillon de données obtenu.

La répartition des fréquences avec les calculs de tous types de fréquences est la suivante :

Exercice 2

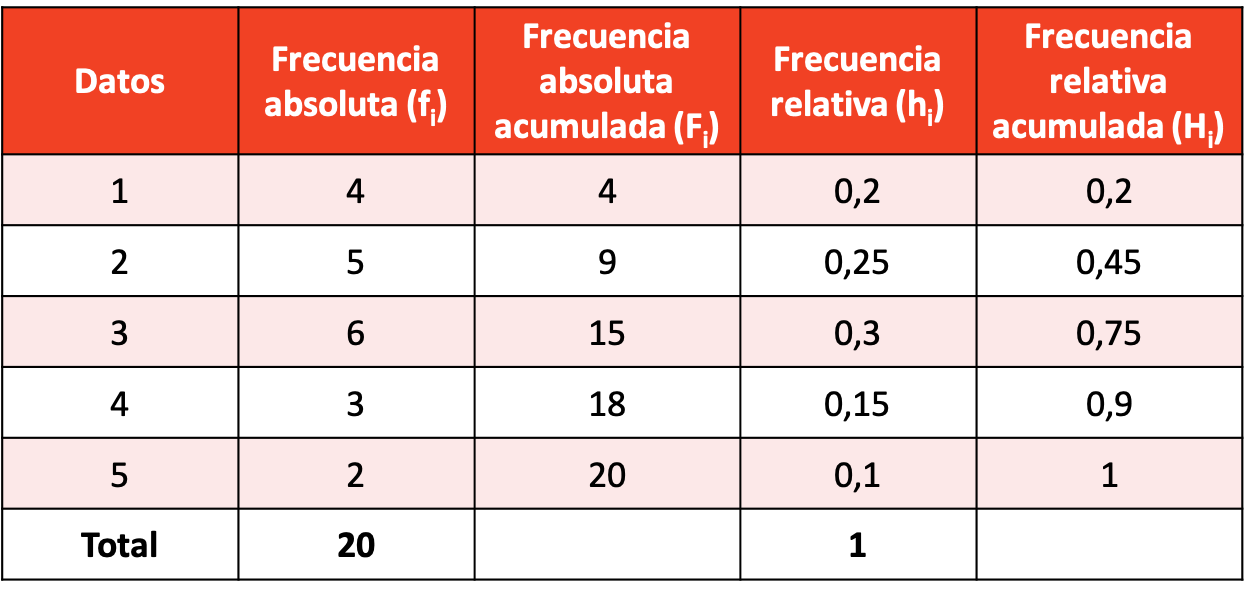
Vous souhaitez faire une étude statistique sur le poids des ouvriers dans une entreprise de 36 salariés. Voici les poids des ouvriers exprimés en kilogrammes :

Construisez une distribution de fréquence avec des données groupées en faisant des intervalles de 5 unités et laissez le premier intervalle être [55,60).

La solution de l’exercice est la distribution de fréquence suivante :