Qu’est-ce que la distribution Erlang ?
La distribution d’Erlang est une distribution de probabilité créée à l’origine par AK Erlang pour modéliser le nombre d’appels téléphoniques qu’un opérateur d’un poste de commutation peut recevoir simultanément.
La distribution est utilisée dans l’ingénierie du trafic téléphonique, les systèmes de files d’attente, la biologie mathématique et d’autres domaines pour modéliser une variété de phénomènes du monde réel.
Propriétés de la distribution Erlang
La distribution d’Erlang a la fonction de densité de probabilité suivante :
f(x; k, μ) = x k-1 e -x/μ / μ k (k-1) !
où:
- k : Le paramètre de forme. Ce doit être un entier positif.
- μ : Le paramètre d’échelle. Ce doit être un nombre réel positif.
Il s’avère que la distribution d’Erlang est un cas particulier de la distribution Gamma lorsque le paramètre de forme k est limité aux seuls entiers réels positifs.
Notez que le paramètre d’échelle est l’inverse du paramètre de taux, λ, c’est-à-dire μ = 1/λ.
La distribution Erlang a les propriétés suivantes :
- Moyenne : k/λ
- Mode : (k-1)/λ
- Écart : k/λ 2
- Asymétrie : 2/√k
- Aplatissement : 6/k
La distribution Erlang a les relations suivantes avec d’autres distributions :
- Lorsque le paramètre de forme k est égal à 1, la distribution d’Erlang est égale à la distribution exponentielle .
- Lorsque le paramètre d’échelle μ est égal à 2, la distribution d’Erlang est égale à une distribution du Chi carré à 2 degrés de liberté.
Visualiser la distribution Erlang
Le graphique suivant montre la forme de la distribution Erlang lorsqu’elle prend différents paramètres :
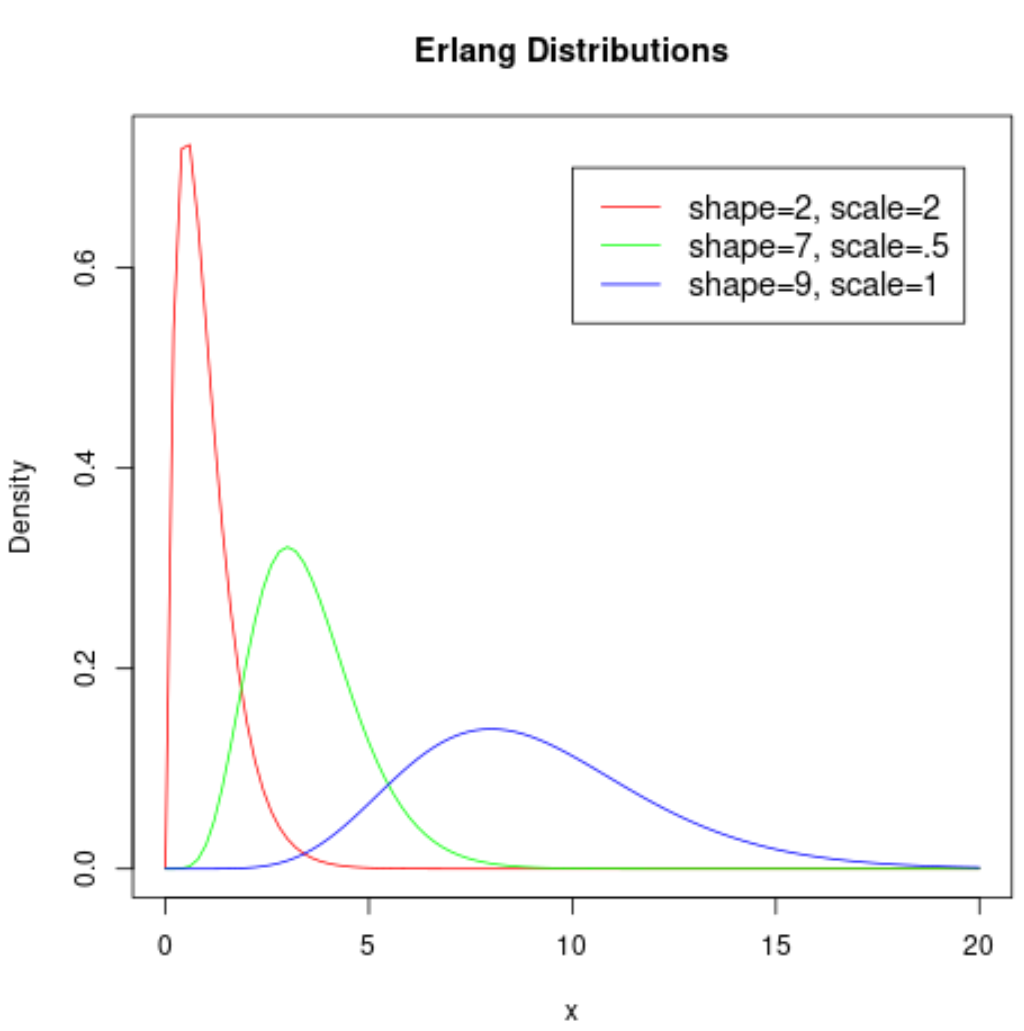
Il est intéressant de voir à quel point la forme de la distribution change en fonction des valeurs utilisées pour les paramètres de forme et d’échelle.
Remarque : Vous pouvez trouver le code R utilisé pour générer le tracé des distributions Erlang ici .
Cas d’utilisation
La distribution Erlang est utilisée dans divers contextes du monde réel, notamment :
1. Centres d’appels
La distribution Erlang est utilisée pour modéliser le temps entre les appels entrants dans un centre d’appels ainsi que le nombre d’appels attendu.
Cela permet aux centres d’appels de savoir quelle devrait être leur capacité en personnel à différents moments de la journée afin de pouvoir traiter les appels entrants en temps opportun sans perdre d’argent en dotant trop d’employés au cours d’un quart de travail donné.
2. Paramètres médicaux
La distribution Erlang est largement utilisée pour modéliser la distribution de la durée du cycle cellulaire, qui a de nombreuses applications différentes en milieu médical.
3. Paramètres de vente au détail
La distribution Erlang est utilisée par les détaillants pour modéliser la fréquence des délais d’achat par les consommateurs.
Cela donne aux détaillants et autres entreprises une idée de la fréquence à laquelle un consommateur donné est censé leur acheter un produit ou un service. Cela aide les entreprises à contrôler les stocks ainsi qu’à recruter du personnel.
Ressources additionnelles
Une introduction à la distribution normale
Une introduction à la distribution binomiale
Une introduction à la distribution de Poisson
à propos de l'auteur
Dr. Benjamin Anderson
Il est un professeur de statistiques à la retraite devenu éducateur dévoué sur Statorials. Avec une vaste expérience et une expertise dans le domaine des statistiques, je m'engage à partager mes connaissances pour responsabiliser les étudiants grâce à Statorials. Lire plus