Que sont les résidus de Pearson ? (Définition & #038; Exemple)
Les résidus de Pearson sont utilisés dans un test d’indépendance du chi carré pour analyser la différence entre le nombre de cellules observé et le nombre de cellules attendu dans un tableau de contingence.
La formule pour calculer un résidu de Pearson est la suivante :
r ij = (O ij – E ij ) / √ E ij
où:
- r ij : Le résidu de Pearson pour la cellule de la i ème colonne et de la j ème ligne
- O ij : La valeur observée pour la cellule de la i ème colonne et de la j ème ligne
- E ij : La valeur attendue pour la cellule de la i ème colonne et de la j ème ligne
Une mesure similaire est le résiduel de Pearson standardisé (ajusté) , qui est calculé comme suit :
r ij = (O ij – E ij ) / √ E ij (1-n i+ )(1-n +j )
où:
- r ij : Le résidu de Pearson pour la cellule de la i ème colonne et de la j ème ligne
- O ij : La valeur observée pour la cellule de la i ème colonne et de la j ème ligne
- E ij : La valeur attendue pour la cellule de la i ème colonne et de la j ème ligne
- p i+ : Le total de la ligne divisé par le total général
- p + j : Le total de la colonne divisé par le total général
Les résidus de Pearson standardisés sont normalement distribués avec une moyenne de 0 et un écart type de 1. Tout résidu de Pearson standardisé avec une valeur absolue supérieure à certains seuils (par exemple 2 ou 3) indique un manque d’ajustement.
L’exemple suivant montre comment calculer les résidus de Pearson dans la pratique.
Exemple : Calcul des résidus de Pearson
Supposons que les chercheurs souhaitent utiliser un test d’indépendance du chi carré pour déterminer si le sexe est associé ou non à la préférence pour un parti politique.
Ils décident de prélever un échantillon aléatoire simple de 500 électeurs et de les interroger sur leur préférence en matière de parti politique.
Le tableau de contingence suivant présente les résultats de l’enquête :
| Républicain | Démocrate | Indépendant | Total | |
| Mâle | 120 | 90 | 40 | 250 |
| Femelle | 110 | 95 | 45 | 250 |
| Total | 230 | 185 | 85 | 500 |
Avant de calculer les résidus de Pearson, nous devons d’abord calculer les comptes attendus pour chaque cellule du tableau de contingence. Pour ce faire, nous pouvons utiliser la formule suivante :
Valeur attendue = (somme des lignes * somme des colonnes) / somme du tableau.
Par exemple, la valeur attendue pour les hommes républicains est : (230*250) / 500 = 115 .
Nous pouvons répéter cette formule pour obtenir la valeur attendue pour chaque cellule du tableau :
| Républicain | Démocrate | Indépendant | Total | |
| Mâle | 115 | 92,5 | 42,5 | 250 |
| Femelle | 115 | 92,5 | 42,5 | 250 |
| Total | 230 | 185 | 85 | 500 |
Ensuite, nous pouvons calculer le résidu de Pearson pour chaque cellule du tableau.
Par exemple, le résidu de Pearson pour la cellule contenant les hommes républicains serait calculé comme suit :
- r ij = (O ij – E ij ) / √ E ij
- r ij = (120 – 115) / √ 115
- r ij = 0,466
Nous pouvons répéter cette formule pour obtenir le résidu de Pearson pour chaque cellule du tableau :
| Républicain | Démocrate | Indépendant | |
| Mâle | 0,446 | -0,259 | -0,383 |
| Femelle | -0,446 | 0,259 | 0,383 |
Ensuite, nous pouvons calculer le résiduel standardisé de Pearson pour chaque cellule du tableau.
Par exemple, le résiduel standardisé de Pearson pour la cellule contenant les hommes républicains serait calculé comme suit :
- r ij = (O ij – E ij ) / √ E ij (1-p i+ )(1-p +j )
- r ij = (120 – 115) / √ 115(1-250/500)(1-230/500)
- r ij = 0,897
Nous pouvons répéter cette formule pour obtenir le résiduel standardisé de Pearson pour chaque cellule du tableau :
| Républicain | Démocrate | Indépendant | |
| Mâle | 0,897 | -0,463 | -0,595 |
| Femelle | -0,897 | 0,463 | 0,595 |
Nous pouvons voir qu’aucun des résidus standardisés de Pearson n’a une valeur absolue supérieure à 3, ce qui indique qu’aucune des cellules ne contribue à un manque d’ajustement significatif.
Si nous utilisons ce calculateur en ligne pour effectuer un test d’indépendance du chi carré, nous constaterons que la valeur p du test est 0,649198 .
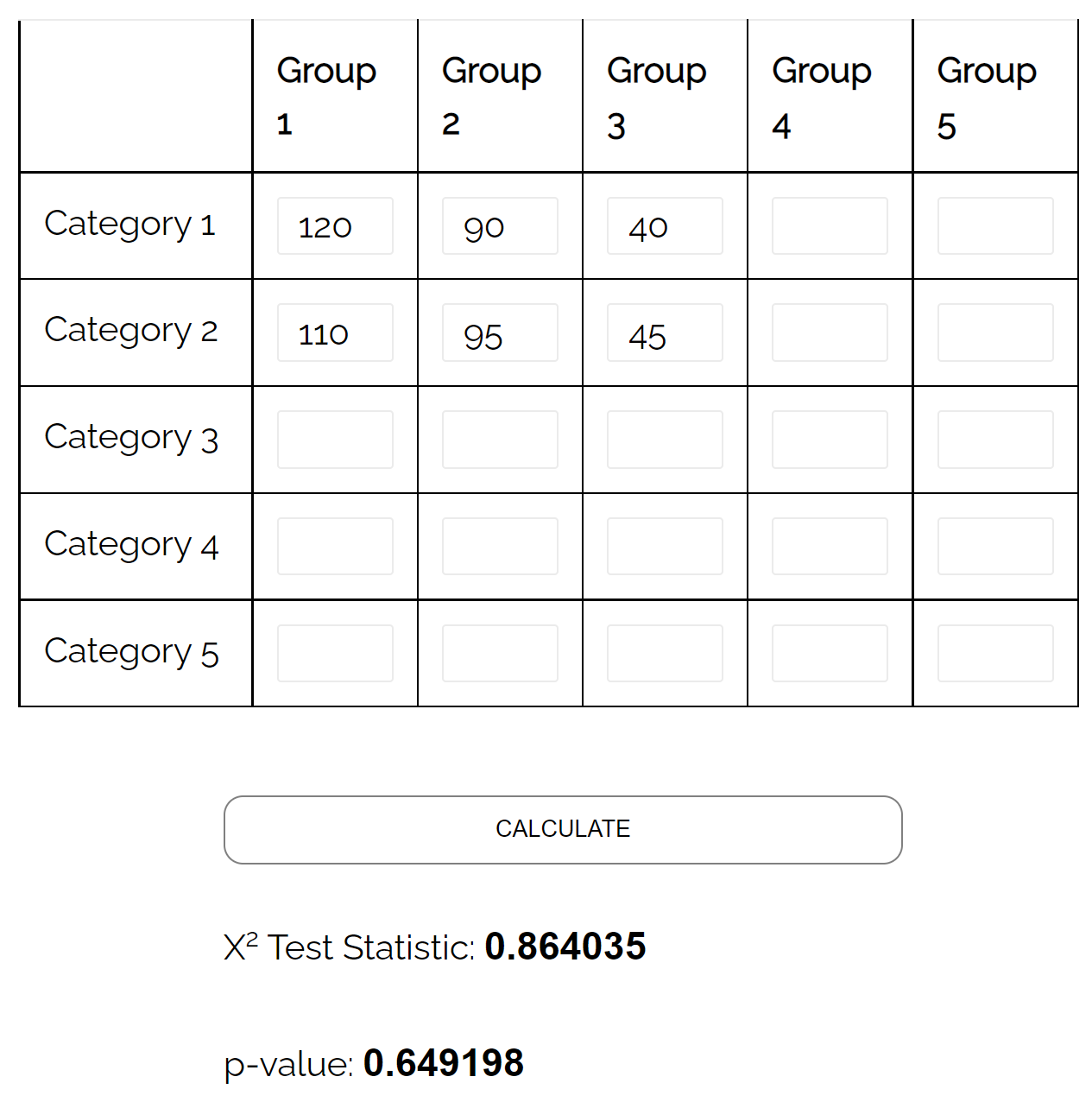
Puisque cette valeur p n’est pas inférieure à 0,05, nous ne disposons pas de preuves suffisantes pour affirmer qu’il existe une association entre le sexe et la préférence pour le parti politique.
Ressources additionnelles
Les didacticiels suivants expliquent comment effectuer un test d’indépendance du chi carré à l’aide de différents logiciels statistiques :
Une introduction au test d’indépendance du chi carré
Comment effectuer un test d’indépendance du chi carré dans Excel
Comment effectuer un test d’indépendance du chi carré dans R
Calculatrice du test du chi carré d’indépendance
