Que sont les résidus standardisés ?

Un résidu est la différence entre une valeur observée et une valeur prédite dans un modèle de régression .

Il est calculé comme suit :

Résiduel = Valeur observée – Valeur prédite

Si nous traçons les valeurs observées et superposons la droite de régression ajustée, les résidus pour chaque observation seraient la distance verticale entre l’observation et la droite de régression :

Un type de résidu que nous utilisons souvent pour identifier les valeurs aberrantes dans un modèle de régression est appelé résidu standardisé .

Il est calculé comme suit :

r _je = e _je / s(e _je ) = e _je / RSE√ 1-h _ii

où:

• e _i : Le i ^ème résidu
• RSE : l’erreur type résiduelle du modèle
• h _ii : Le levier de la ^ième observation

En pratique, on considère souvent tout résidu standardisé dont la valeur absolue est supérieure à 3 comme une valeur aberrante.

Cela ne signifie pas nécessairement que nous supprimerons ces observations du modèle, mais nous devrions au moins les étudier plus en profondeur pour vérifier qu’elles ne résultent pas d’une erreur de saisie de données ou d’un autre événement étrange.

Remarque : Parfois, les résidus standardisés sont également appelés « résidus étudiés en interne ».

Exemple : Comment calculer les résidus standardisés

Supposons que nous ayons l’ensemble de données suivant avec 12 observations au total :

Si nous utilisons un logiciel statistique (comme R , Excel , Python , Stata , etc.) pour ajuster une ligne de régression linéaire à cet ensemble de données, nous constaterons que la ligne de meilleur ajustement s’avère être :

y = 29,63 + 0,7553x

En utilisant cette ligne, nous pouvons calculer la valeur prédite pour chaque valeur Y en fonction de la valeur de X. Par exemple, la valeur prédite de la première observation serait :

y = 29,63 + 0,7553*(8) = 35,67

Nous pouvons alors calculer le résidu pour cette observation comme suit :

Résiduel = Valeur observée – Valeur prédite = 41 – 35,67 = 5,33

Nous pouvons répéter ce processus pour trouver le résidu pour chaque observation :

Nous pouvons également utiliser un logiciel statistique pour constater que l’erreur type résiduelle du modèle est de 4,44 .

Et, bien que cela dépasse le cadre de ce didacticiel, nous pouvons utiliser un logiciel pour trouver la statistique de levier (h _ii ) pour chaque observation :

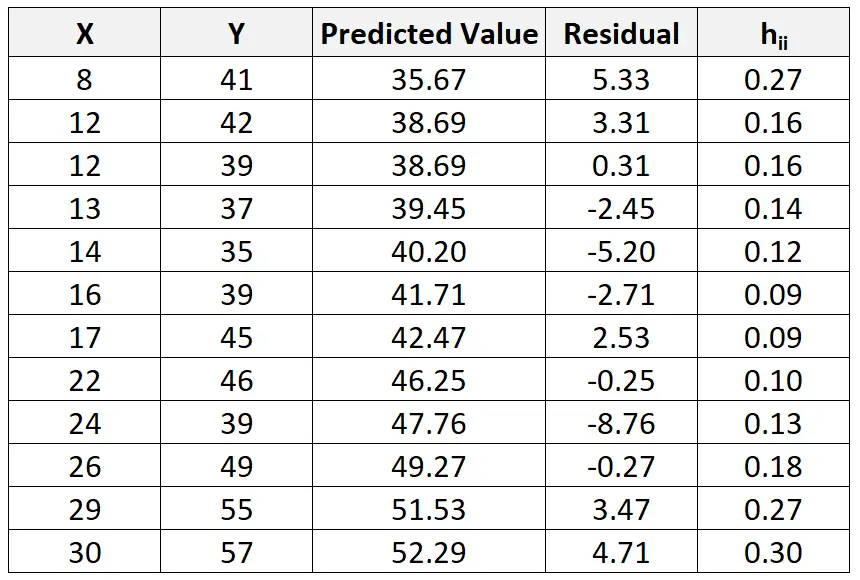
On peut alors utiliser la formule suivante pour calculer le résidu standardisé pour chaque observation :

r _je = e _je / RSE√ 1-h _ii

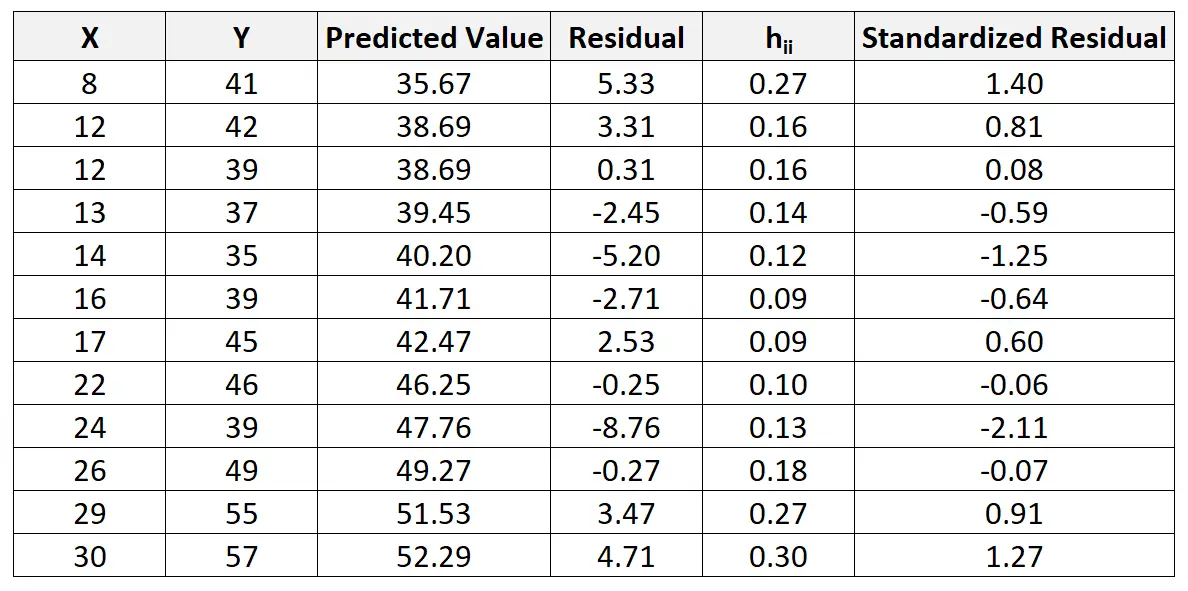
Par exemple, le résidu standardisé pour la première observation est calculé comme suit :

r _je = 5,33 / 4,44√ 1-0,27 = 1,404

Nous pouvons répéter ce processus pour trouver le résidu standardisé pour chaque observation :

Nous pouvons ensuite créer un nuage de points rapide des valeurs prédictives par rapport aux résidus standardisés pour voir visuellement si l’un des résidus standardisés dépasse un seuil de valeur absolue de 3 :

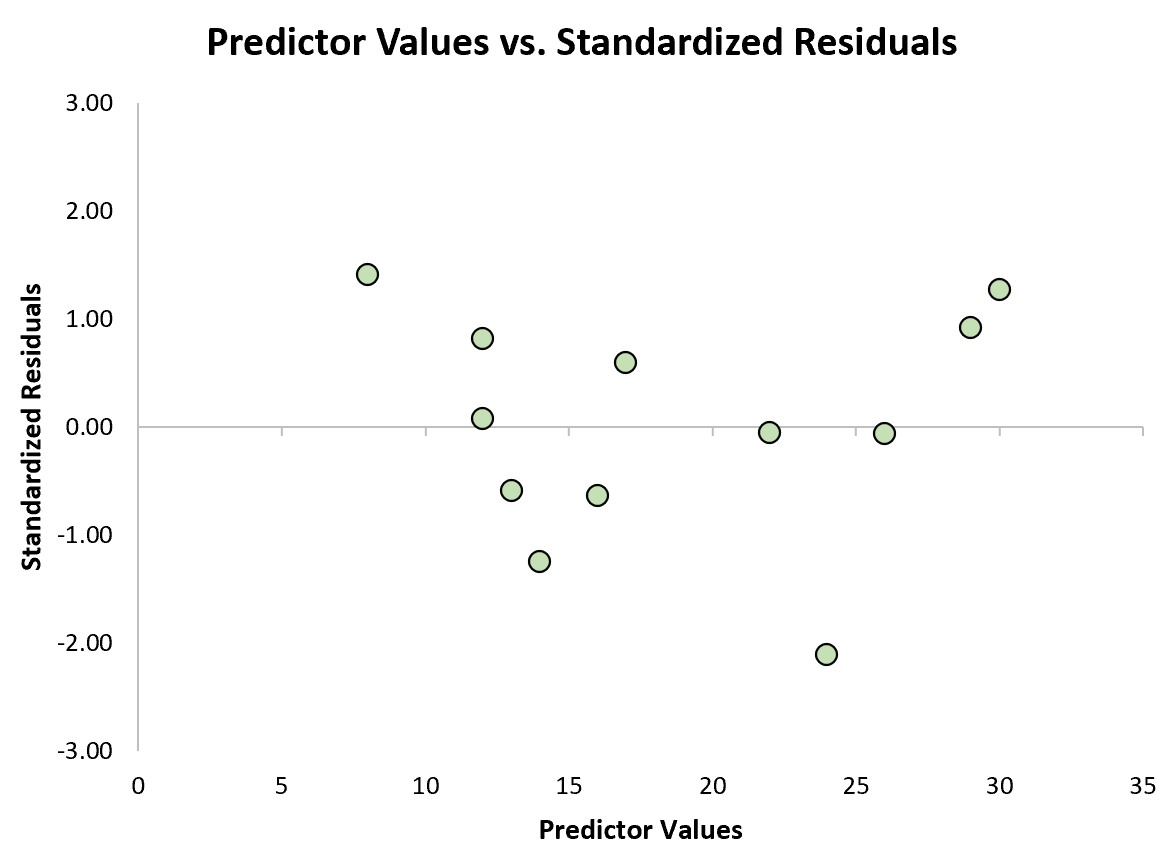
D’après le graphique, nous pouvons voir qu’aucun des résidus standardisés ne dépasse une valeur absolue de 3. Ainsi, aucune des observations ne semble être aberrante.

Il convient de noter que dans certains cas, les chercheurs considèrent comme aberrantes les observations dont les résidus standardisés dépassent une valeur absolue de 2.

C’est à vous de décider, en fonction du domaine dans lequel vous travaillez et du problème spécifique sur lequel vous travaillez, si vous souhaitez utiliser une valeur absolue de 2 ou 3 comme seuil des valeurs aberrantes.

Ressources additionnelles

Les didacticiels suivants fournissent des informations supplémentaires sur les résidus standardisés :

Que sont les résidus dans les statistiques ?
Comment calculer les résidus standardisés dans Excel
Comment calculer les résidus standardisés dans R
Comment calculer les résidus standardisés en Python