Sélection aléatoire ou attribution aléatoire

La sélection aléatoire et l’assignation aléatoire sont deux techniques statistiques couramment utilisées, mais souvent confondues.

La sélection aléatoire fait référence au processus de sélection aléatoire d’individus dans une population qui seront impliqués dans une étude.

L’assignation aléatoire fait référence au processus d’ attribution aléatoire des individus participant à une étude à un groupe de traitement ou à un groupe témoin.

Vous pouvez considérer la sélection aléatoire comme le processus que vous utilisez pour « obtenir » les individus dans une étude et vous pouvez considérer l’assignation aléatoire comme ce que vous « faites » avec ces individus une fois qu’ils sont sélectionnés pour faire partie de l’étude.

L’importance de la sélection aléatoire et de l’attribution aléatoire

Lorsqu’une étude utilise la sélection aléatoire , elle sélectionne des individus dans une population à l’aide d’un processus aléatoire. Par exemple, si une population compte 1 000 individus, nous pourrions utiliser un ordinateur pour sélectionner au hasard 100 de ces individus dans une base de données. Cela signifie que chaque individu a la même probabilité d’être sélectionné pour faire partie de l’étude, ce qui augmente les chances d’obtenir un échantillon représentatif – un échantillon présentant des caractéristiques similaires à celles de la population globale.

En utilisant un échantillon représentatif dans notre étude, nous sommes en mesure de généraliser les résultats de notre étude à la population. En termes statistiques, cela s’appelle avoir une validité externe – il est valable d’externaliser nos résultats à la population globale.

Lorsqu’une étude utilise l’assignation aléatoire , elle assigne au hasard les individus à un groupe de traitement ou à un groupe témoin. Par exemple, si nous avons 100 individus dans une étude, nous pourrions utiliser un générateur de nombres aléatoires pour attribuer au hasard 50 individus à un groupe témoin et 50 individus à un groupe de traitement.

En utilisant l’assignation aléatoire, nous augmentons les chances que les deux groupes aient des caractéristiques à peu près similaires, ce qui signifie que toute différence observée entre les deux groupes peut être attribuée au traitement. Cela signifie que l’étude a une validité interne : il est valable d’attribuer toute différence entre les groupes au traitement lui-même, par opposition aux différences entre les individus des groupes.

Exemples de sélection aléatoire et d’attribution aléatoire

Il est possible qu’une étude utilise à la fois la sélection aléatoire et l’assignation aléatoire, ou une seule de ces techniques, ou aucune des deux techniques. Une étude solide est celle qui utilise les deux techniques.

Les exemples suivants montrent comment une étude pourrait utiliser les deux, l’une ou aucune de ces techniques, ainsi que les effets qui en découlent.

Exemple 1 : Utilisation à la fois de la sélection aléatoire et de l’attribution aléatoire

Étude : Les chercheurs veulent savoir si un nouveau régime entraîne une perte de poids plus importante qu’un régime standard dans une certaine communauté de 10 000 personnes. Ils recrutent 100 personnes pour participer à l’étude en utilisant un ordinateur pour sélectionner au hasard 100 noms dans une base de données. Une fois qu’ils ont les 100 individus, ils utilisent à nouveau un ordinateur pour assigner au hasard 50 individus à un groupe témoin (par exemple s’en tenir à leur régime alimentaire standard) et 50 individus à un groupe de traitement (par exemple suivre le nouveau régime). Ils enregistrent la perte de poids totale de chaque individu après un mois.

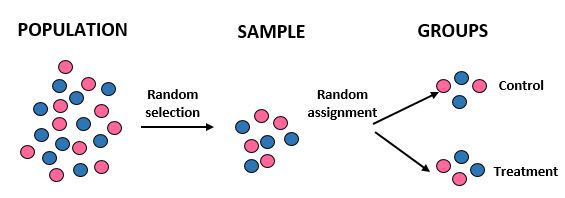
Résultats : Les chercheurs ont utilisé une sélection aléatoire pour obtenir leur échantillon et leur assignation aléatoire lorsqu’ils ont placé les individus dans un groupe de traitement ou un groupe témoin. Ce faisant, ils sont en mesure de généraliser les résultats de l’étude à la population globale et d’attribuer les différences de perte de poids moyenne entre les deux groupes au nouveau régime.

Exemple 2 : Utiliser uniquement la sélection aléatoire

Étude : Les chercheurs veulent savoir si un nouveau régime entraîne une perte de poids plus importante qu’un régime standard dans une certaine communauté de 10 000 personnes. Ils recrutent 100 personnes pour participer à l’étude en utilisant un ordinateur pour sélectionner au hasard 100 noms dans une base de données. Cependant, ils décident de répartir les individus dans des groupes basés uniquement sur leur sexe. Les femmes sont affectées au groupe témoin et les hommes au groupe de traitement. Ils enregistrent la perte de poids totale de chaque individu après un mois.

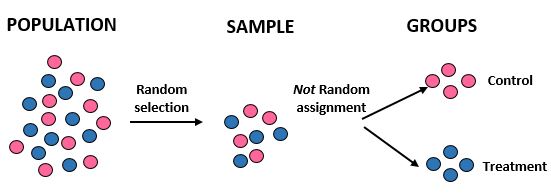
Résultats : Les chercheurs ont utilisé une sélection aléatoire pour obtenir leur échantillon, mais ils n’ont pas eu recours à l’assignation aléatoire lorsqu’ils ont placé les individus dans un groupe de traitement ou dans un groupe témoin. Au lieu de cela, ils ont utilisé un facteur spécifique – le sexe – pour décider à quel groupe attribuer les individus. Ce faisant, ils sont en mesure de généraliser les résultats de l’étude à la population globale, mais ils ne sont pas en mesure d’attribuer au nouveau régime les différences de perte de poids moyenne entre les deux groupes. La validité interne de l’étude a été compromise car la différence de perte de poids pourrait en réalité être simplement due au sexe plutôt qu’au nouveau régime.

Exemple 3 : Utiliser uniquement l’attribution aléatoire

Étude : Les chercheurs veulent savoir si un nouveau régime entraîne une perte de poids plus importante qu’un régime standard dans une certaine communauté de 10 000 personnes. Ils recrutent 100 athlètes masculins pour participer à l’étude. Ensuite, ils utilisent un programme informatique pour attribuer au hasard 50 athlètes masculins à un groupe témoin et 50 au groupe de traitement. Ils enregistrent la perte de poids totale de chaque individu après un mois.

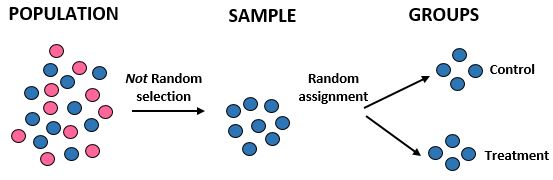
Résultats : Les chercheurs n’ont pas utilisé de sélection aléatoire pour obtenir leur échantillon puisqu’ils ont spécifiquement choisi 100 athlètes masculins. Pour cette raison, leur échantillon n’est pas représentatif de la population globale et leur validité externe est donc compromise – ils ne pourront pas généraliser les résultats de l’étude à la population globale. Cependant, ils ont utilisé une répartition aléatoire, ce qui signifie qu’ils peuvent attribuer toute différence de perte de poids au nouveau régime.

Exemple 4 : utiliser aucune des deux techniques

Étude : Les chercheurs veulent savoir si un nouveau régime entraîne une perte de poids plus importante qu’un régime standard dans une certaine communauté de 10 000 personnes. Ils recrutent 50 athlètes masculins et 50 athlètes féminines pour participer à l’étude. Ensuite, ils assignent toutes les athlètes féminines au groupe témoin et tous les athlètes masculins au groupe de traitement. Ils enregistrent la perte de poids totale de chaque individu après un mois.

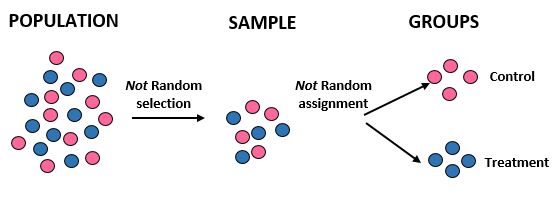
Résultats : Les chercheurs n’ont pas utilisé de sélection aléatoire pour obtenir leur échantillon puisqu’ils ont spécifiquement choisi 100 athlètes. Pour cette raison, leur échantillon n’est pas représentatif de la population globale et leur validité externe est donc compromise – ils ne pourront pas généraliser les résultats de l’étude à la population globale. En outre, ils divisent les individus en groupes en fonction du sexe plutôt que de recourir à une assignation aléatoire, ce qui signifie que leur validité interne est également compromise – les différences de perte de poids pourraient être dues au sexe plutôt qu’au régime alimentaire.