Comment interpréter Sig. Valeurs (bilatérales) dans SPSS

Souvent, lorsque vous effectuez des tests statistiques dans SPSS, la table de sortie contient un Sig. valeur (bilatérale) .

Cette valeur représente la valeur p bilatérale du test.

Si cette valeur est inférieure à votre niveau de signification (les choix courants sont 0,05 ou 0,01), vous pouvez alors rejeter l’hypothèse nulle de votre test.

Ce didacticiel fournit des exemples sur la façon d’interpréter le Sig. valeur (bilatérale) de différents tests statistiques.

Exemple 1 : test t sur un échantillon

Un test t sur un échantillon est utilisé pour tester si la moyenne d’une population est égale ou non à une certaine valeur.

Par exemple, supposons qu’un botaniste veuille savoir si la hauteur moyenne d’une certaine espèce de plante est égale à 15 pouces. Elle prélève un échantillon aléatoire de 12 plantes et enregistre chacune de leurs hauteurs en pouces.

Elle utilise ensuite cet échantillon pour effectuer un test t sur un échantillon avec les hypothèses nulles et alternatives suivantes :

• H ₀ : μ = 15 (la moyenne réelle de la population est égale à 15 pouces)
• H _A : μ ≠ 15 (la moyenne réelle de la population n’est pas égale à 15 pouces)

Elle effectue ce test t sur un échantillon dans SPSS et obtient les résultats suivants :

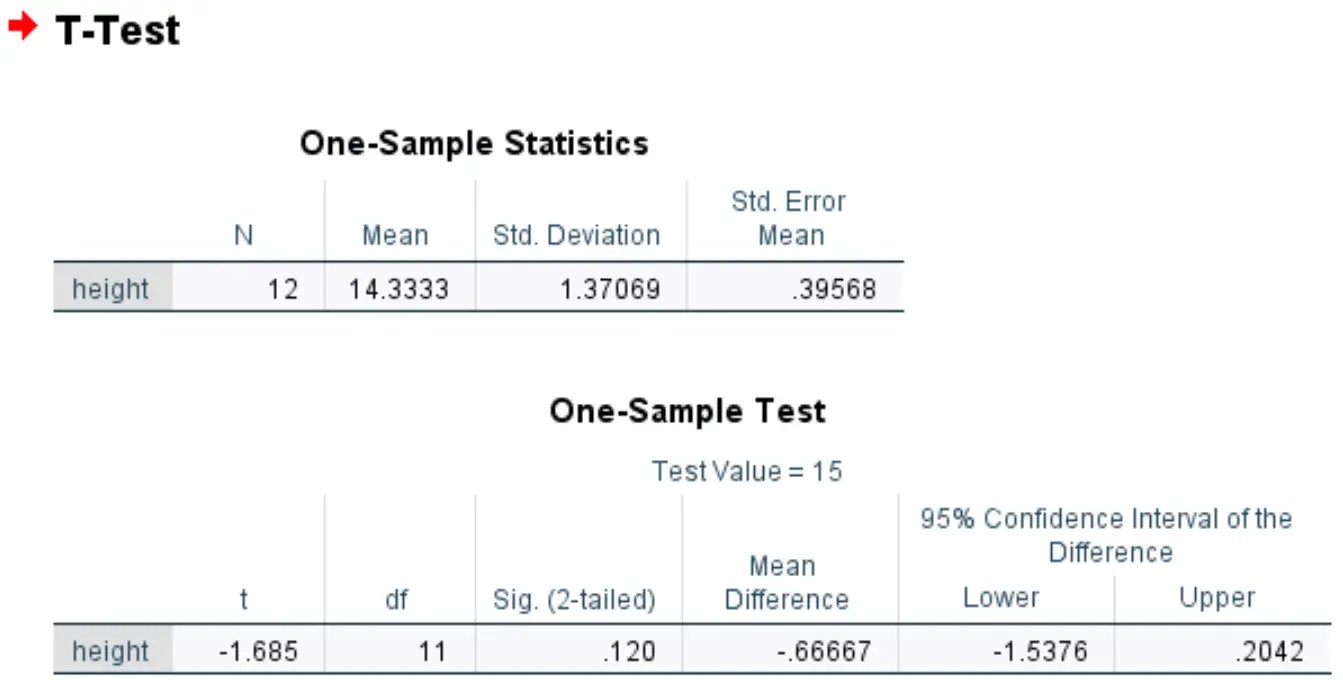
Le Sig. La valeur (bilatérale) est 0,120 .

Cela représente la valeur p bilatérale qui correspond à une valeur de -1,685 avec 11 degrés de liberté.

Puisque la valeur p du test (0,120) n’est pas inférieure à 0,05, nous ne parvenons pas à rejeter l’hypothèse nulle.

En d’autres termes, nous n’avons pas suffisamment de preuves pour affirmer que la véritable hauteur moyenne de cette espèce de plante est différente de 15 pouces.

Exemple 2 : test t à deux échantillons

Un test t à deux échantillons est utilisé pour tester si les valeurs moyennes de deux populations sont égales ou non.

Par exemple, supposons que les chercheurs souhaitent savoir si un nouveau traitement du carburant entraîne une modification du kilométrage moyen par gallon d’une voiture donnée. Pour tester cela, ils mènent une expérience dans laquelle 12 voitures reçoivent le nouveau traitement de carburant et 12 voitures ne le reçoivent pas.

Les chercheurs effectuent un test t à deux échantillons avec les hypothèses nulles et alternatives suivantes :

• H ₀ : μ ₁ = μ ₂ (le mpg moyen entre les deux populations est égal)
• H ₁ : μ ₁ ≠ μ ₂ (le mpg moyen entre les deux populations n’est pas égal)

Ils effectuent un test t à deux échantillons dans SPSS et obtiennent les résultats suivants :

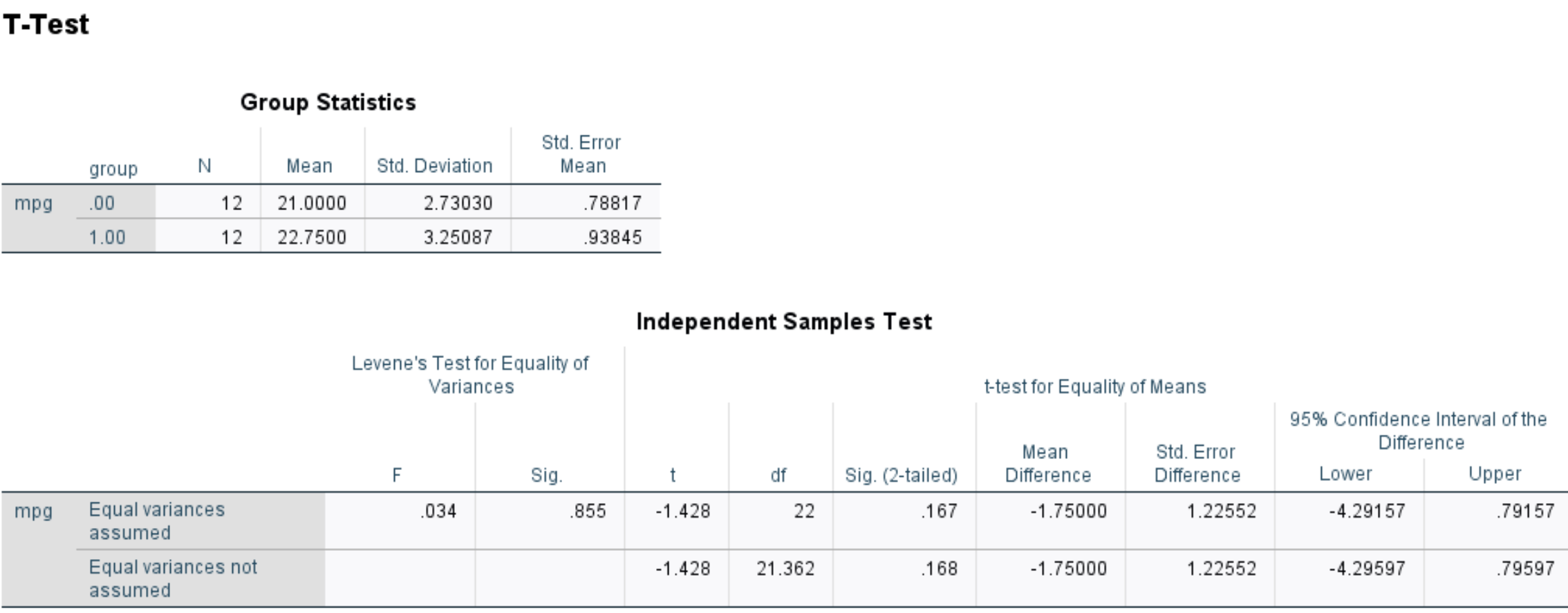
Le Sig. La valeur (bilatérale) est 0,167 .

Cela représente la valeur p bilatérale qui correspond à une valeur de -1,428 avec 22 degrés de liberté.

Puisque la valeur p du test (0,167) n’est pas inférieure à 0,05, nous ne parvenons pas à rejeter l’hypothèse nulle.

En d’autres termes, nous n’avons pas suffisamment de preuves pour affirmer que le véritable mpg moyen est différent entre les voitures qui reçoivent un traitement et celles qui ne le font pas.

Ressources additionnelles

Les didacticiels suivants expliquent comment effectuer divers tests statistiques dans SPSS :

Comment effectuer un test t sur un échantillon dans SPSS
Comment effectuer un test t à deux échantillons dans SPSS
Comment effectuer un test t pour échantillons appariés dans SPSS