Comment calculer la corrélation de classement de Spearman dans Google Sheets
En statistique, la corrélation fait référence à la force et à la direction d’une relation entre deux variables. La valeur d’un coefficient de corrélation peut aller de -1 à 1, avec les interprétations suivantes :
- -1 : une relation négative parfaite entre deux variables
- 0 : aucune relation entre deux variables
- 1 : une relation positive parfaite entre deux variables
Un type spécial de corrélation est appelé corrélation de rang de Spearman , qui est utilisé pour mesurer la corrélation entre deux variables classées. (par exemple, le rang de la note à l’examen de mathématiques d’un élève par rapport au rang de sa note à l’examen de sciences dans une classe).
Ce tutoriel explique comment calculer la corrélation de rang de Spearman entre deux variables dans Google Sheets.
Exemple : corrélation de classement de Spearman dans Google Sheets
Effectuez les étapes suivantes pour calculer la corrélation de rang de Spearman entre la note à l’examen de mathématiques et la note à l’examen de sciences de 10 élèves d’une classe particulière.
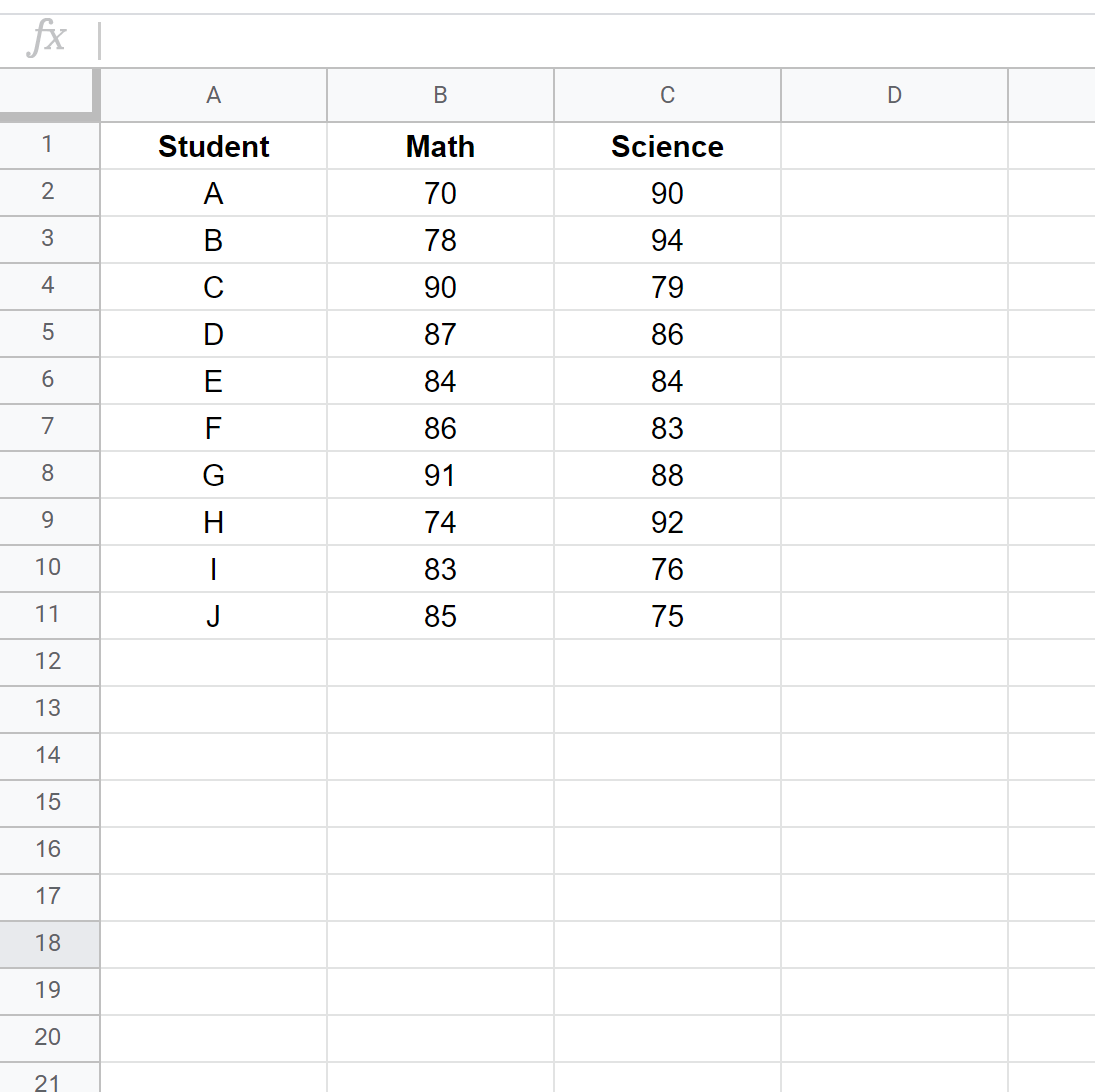
Étape 1 : Saisissez les données.
Saisissez les résultats des examens de chaque étudiant dans deux colonnes distinctes :
Étape 2 : Calculez les classements pour chaque note d’examen.
Ensuite, nous calculerons le classement pour chaque note d’examen. Utilisez les formules suivantes dans les cellules D2 et E2 pour calculer les classements en mathématiques et en sciences du premier élève :
Cellule D2 : =RANK.AVG(B2, $B$2 :$B$11, 0)
Cellule E2 : =RANK.AVG(C2, $C$2 :$C$11, 0)
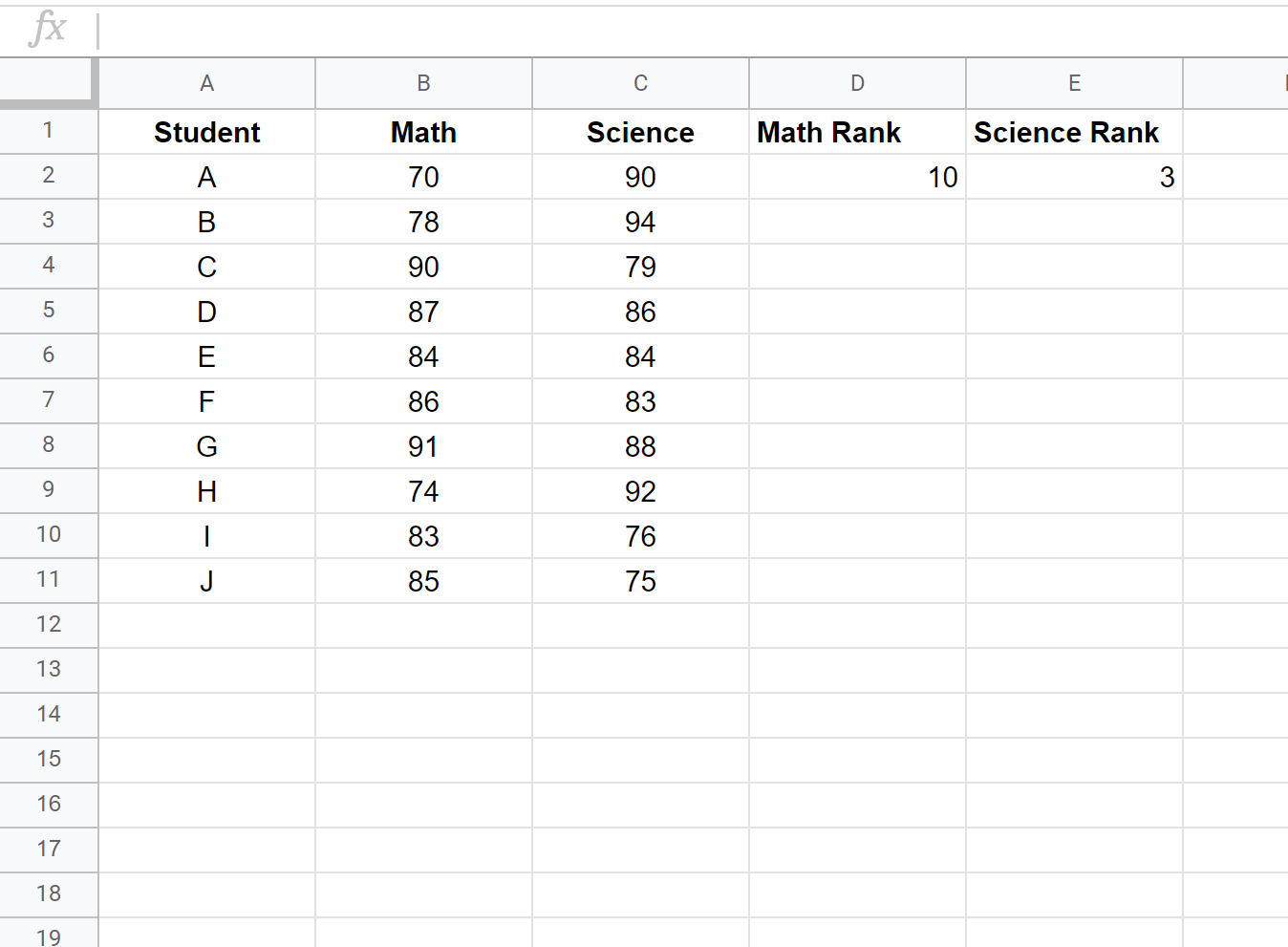
Ensuite, mettez en surbrillance les cellules restantes à remplir :
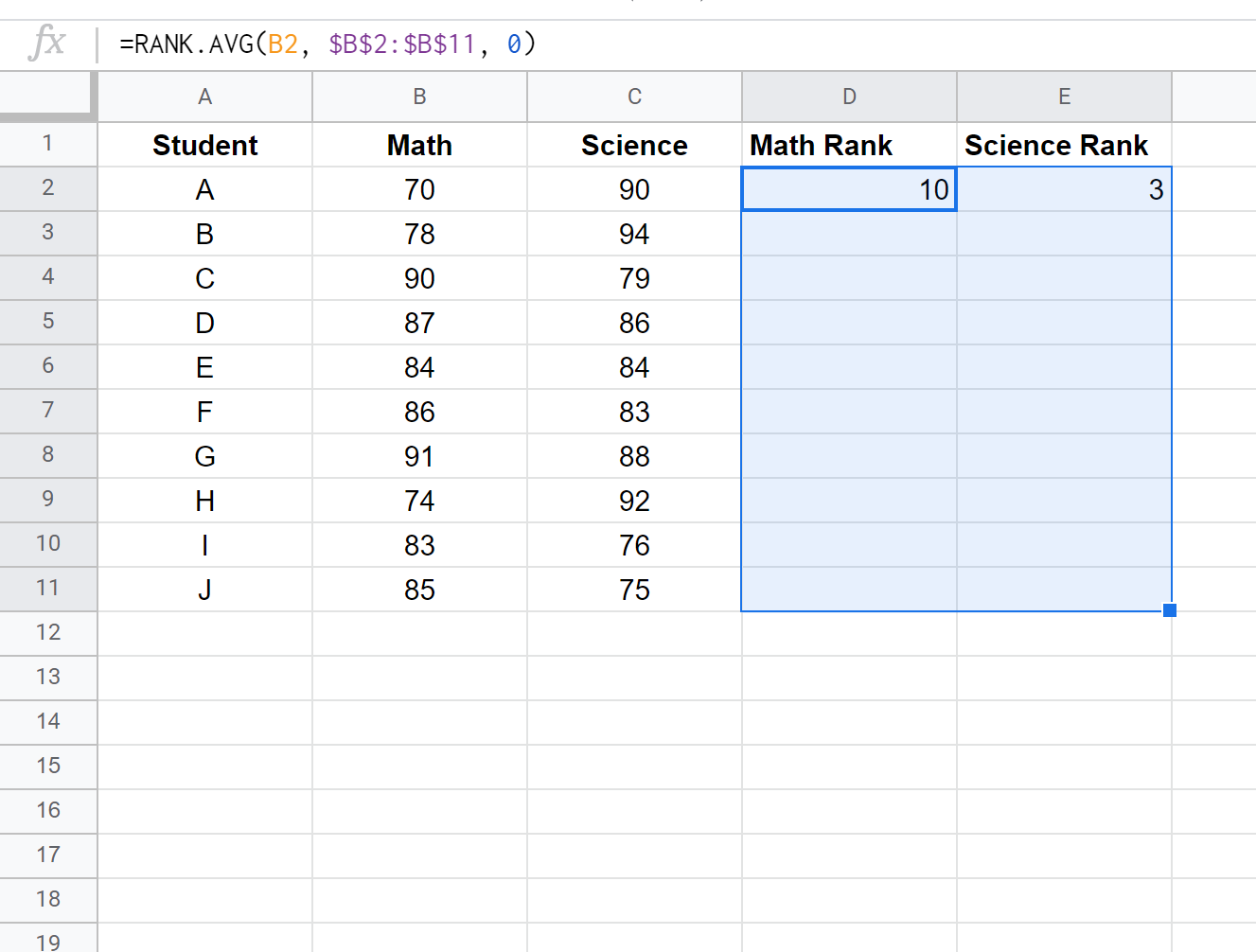
Cliquez ensuite sur Ctrl+D pour renseigner les classements de chaque élève :
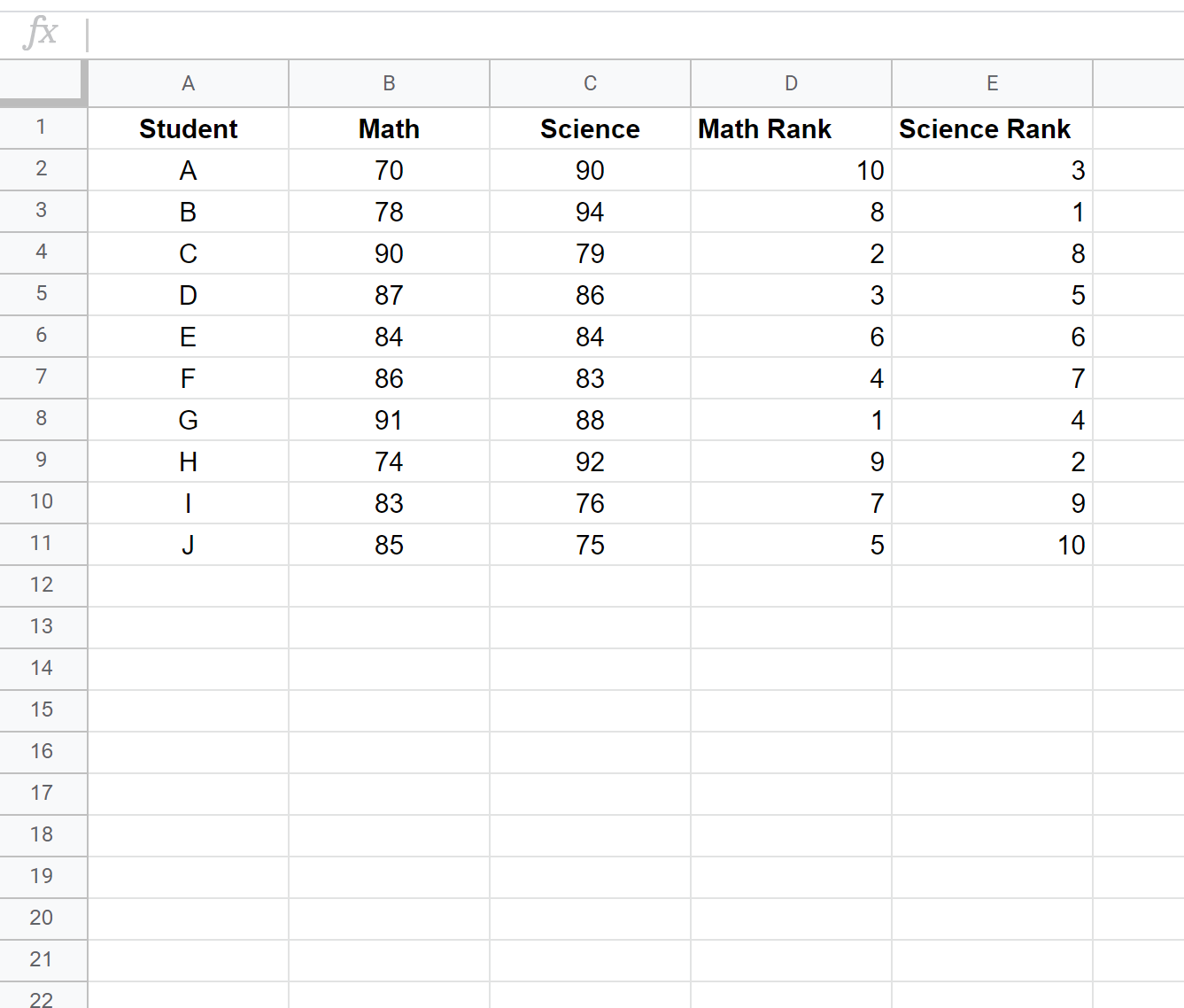
Étape 3 : Calculez le coefficient de corrélation de rang de Spearman.
Enfin, nous calculerons le coefficient de corrélation de rang de Spearman entre les scores en mathématiques et les scores en sciences en utilisant la fonction CORREL() :
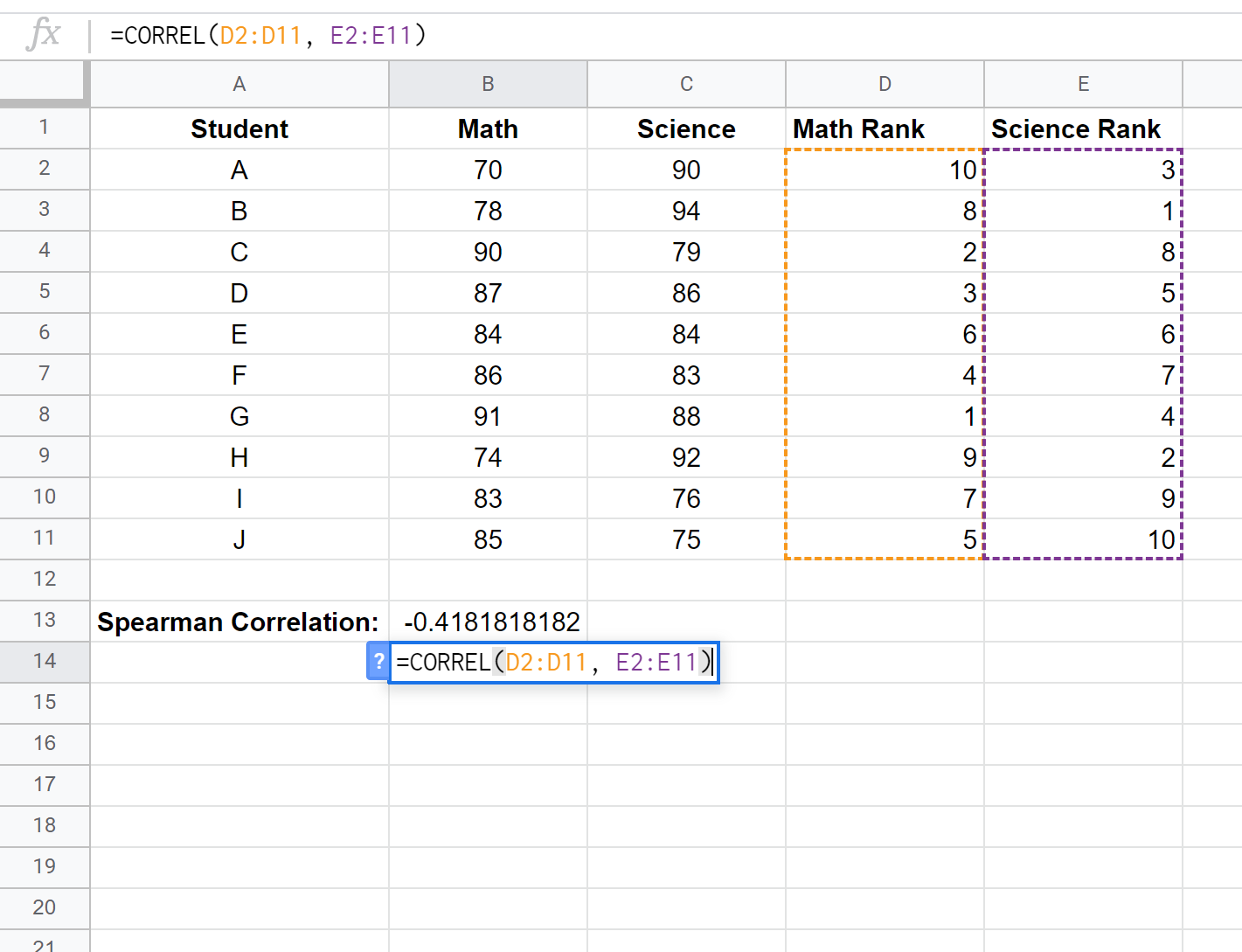
La corrélation des rangs de Spearman s’avère être de -0,41818 .
Étape 4 (Facultatif) : Déterminez si la corrélation des rangs de Spearman est statistiquement significative.
À l’étape précédente, nous avons constaté que la corrélation de rang de Spearman entre les résultats des examens de mathématiques et de sciences était de -0,41818 , ce qui indique une corrélation négative entre les deux variables.
Cependant, pour déterminer si cette corrélation est statistiquement significative, nous aurions besoin de nous référer à un tableau de corrélation des rangs de Spearman des valeurs critiques, qui montre les valeurs critiques associées à différentes tailles d’échantillon (n) et niveaux de signification (α).
Si la valeur absolue de notre coefficient de corrélation est supérieure à la valeur critique du tableau, alors la corrélation entre les deux variables est statistiquement significative.
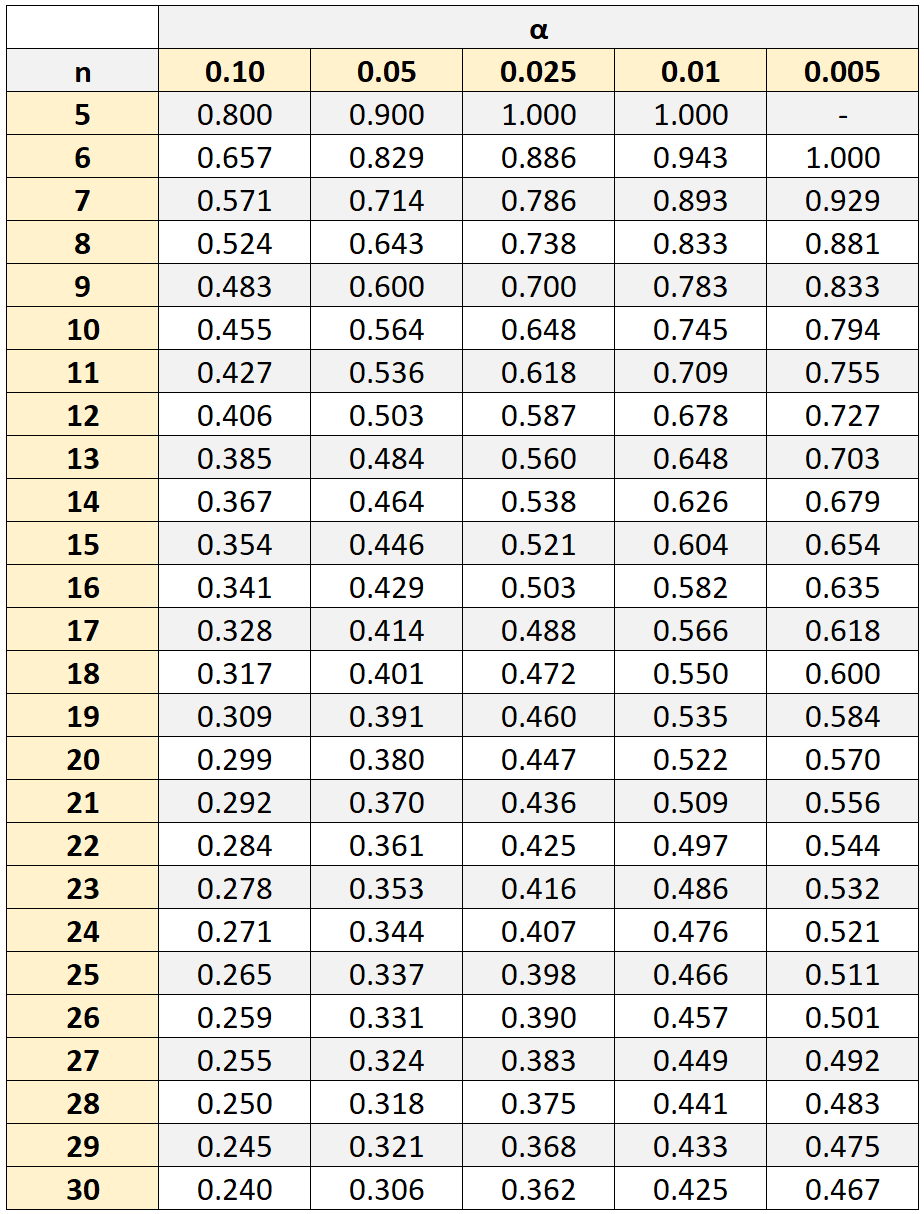
Dans notre exemple, la taille de notre échantillon était de n = 10 étudiants. En utilisant un niveau de signification de 0,05, nous constatons que la valeur critique est de 0,564 .
Étant donné que la valeur absolue du coefficient de corrélation de rang de Spearman que nous avons calculé ( 0,41818 ) n’est pas supérieure à cette valeur critique, cela signifie que la corrélation entre les scores en mathématiques et en sciences n’est pas statistiquement significative.
Connexes : Comment calculer la corrélation des classements Spearman dans Excel
