Un guide doux sur la somme des carrés : SST, SSR, SSE

La régression linéaire est utilisée pour trouver une ligne qui « correspond » le mieux à un ensemble de données.

Nous utilisons souvent trois valeurs de somme des carrés différentes pour mesurer dans quelle mesure la droite de régression s’adapte réellement aux données :

1. Somme des carrés totaux (SST) – La somme des carrés des différences entre les points de données individuels (y _i ) et la moyenne de la variable de réponse ( y ).

• SST = Σ(y _je – y ) ²

2. Régression de la somme des carrés (SSR) – La somme des carrés des différences entre les points de données prédits (ŷ _i ) et la moyenne de la variable de réponse ( y ).

• SSR = Σ(ŷ _je – y ) ²

3. Erreur de somme des carrés (SSE) – La somme des carrés des différences entre les points de données prédits (ŷ _i ) et les points de données observés (y _i ).

• SSE = Σ(ŷ _je – y _je ) ²

La relation suivante existe entre ces trois mesures :

SST = SSR + SSE

Ainsi, si nous connaissons deux de ces mesures, nous pouvons alors utiliser une algèbre simple pour calculer la troisième.

SSR, SST et R-Carré

Le R au carré , parfois appelé coefficient de détermination, est une mesure de l’adéquation d’un modèle de régression linéaire à un ensemble de données. Il représente la proportion de la variance de la variable de réponse qui peut être expliquée par la variable prédictive.

La valeur du R au carré peut varier de 0 à 1. Une valeur de 0 indique que la variable de réponse ne peut pas du tout être expliquée par la variable prédictive. Une valeur de 1 indique que la variable de réponse peut être parfaitement expliquée sans erreur par la variable prédictive.

En utilisant SSR et SST, nous pouvons calculer le R au carré comme suit :

R au carré = SSR / SST

Par exemple, si le SSR pour un modèle de régression donné est de 137,5 et le SST de 156, nous calculerons le R au carré comme suit :

R au carré = 137,5 / 156 = 0,8814

Cela nous indique que 88,14 % de la variation de la variable de réponse peut être expliquée par la variable prédictive.

Calculer SST, SSR, SSE : exemple étape par étape

Supposons que nous ayons l’ensemble de données suivant qui montre le nombre d’heures étudiées par six étudiants différents ainsi que leurs résultats à l’examen final :

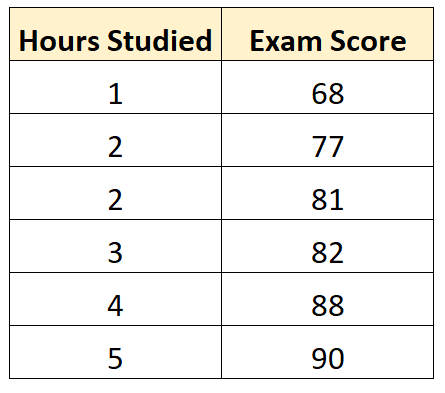
En utilisant certains logiciels statistiques (comme R , Excel , Python ) ou même à la main , nous pouvons constater que la droite la mieux ajustée est :

Score = 66,615 + 5,0769*(Heures)

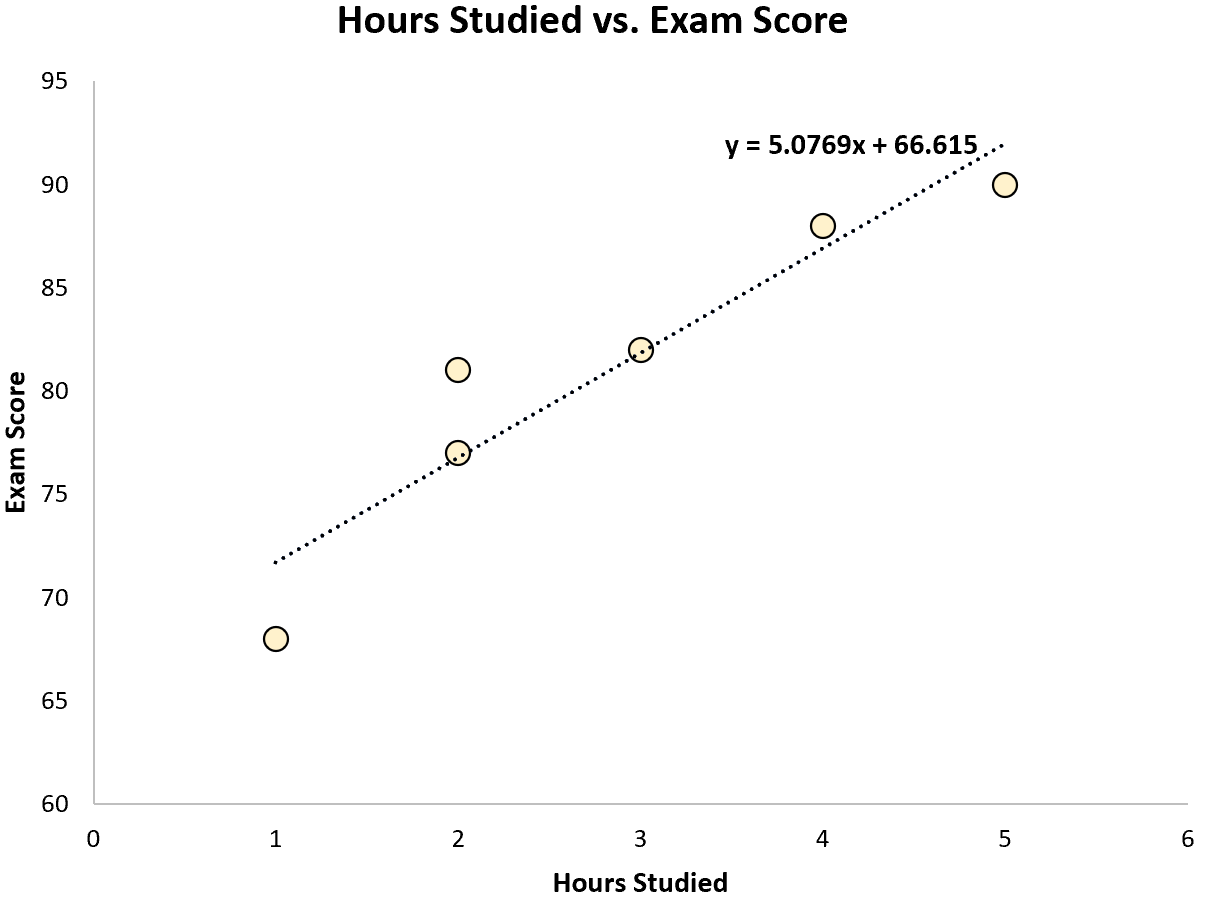
Une fois que nous connaissons la droite de l’équation la mieux ajustée, nous pouvons utiliser les étapes suivantes pour calculer SST, SSR et SSE :

Étape 1 : Calculez la moyenne de la variable de réponse.

La moyenne de la variable de réponse ( y ) s’avère être 81 .

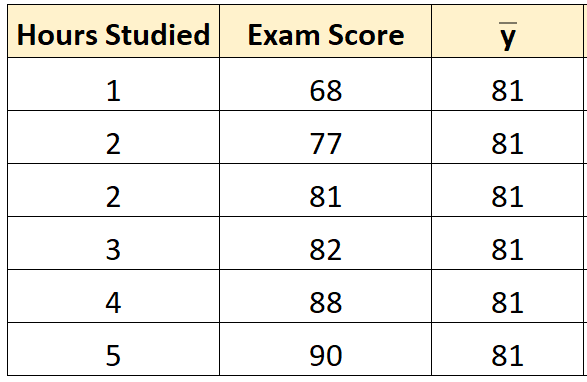
Étape 2 : Calculez la valeur prédite pour chaque observation.

Ensuite, nous pouvons utiliser la droite de l’équation la mieux adaptée pour calculer la note prévue à l’examen () pour chaque étudiant.

Par exemple, la note prévue à l’examen pour l’étudiant qui a étudié une heure est :

Note = 66,615 + 5,0769*(1) = 71,69 .

Nous pouvons utiliser la même approche pour trouver le score prédit pour chaque élève :

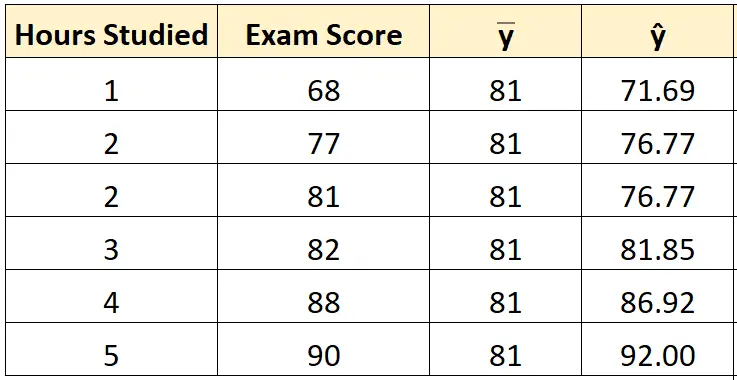
Étape 3 : Calculez la somme des carrés totale (SST).

Ensuite, nous pouvons calculer la somme des carrés au total.

Par exemple, la somme des carrés totale pour le premier élève est :

(y _je – y ) ² = (68 – 81) ² = 169 .

Nous pouvons utiliser la même approche pour trouver la somme des carrés totale pour chaque élève :

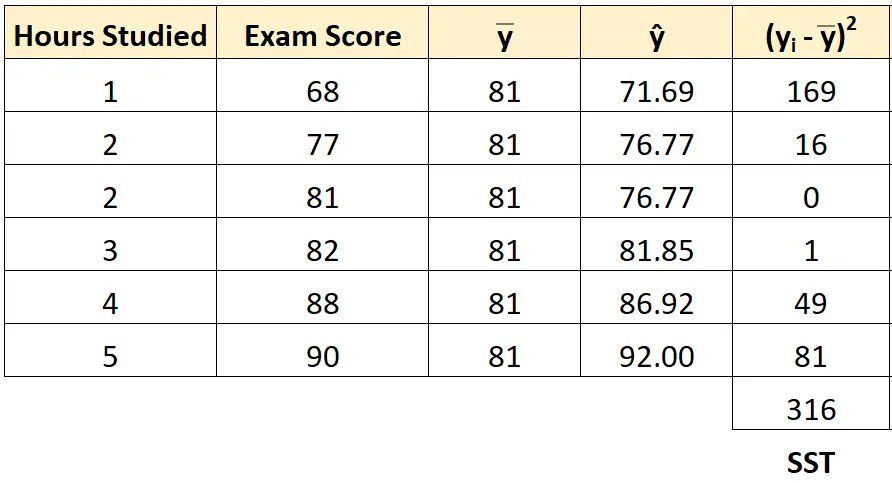
La somme totale des carrés s’avère être 316 .

Étape 4 : Calculez la régression de la somme des carrés (SSR).

Ensuite, nous pouvons calculer la régression de la somme des carrés.

Par exemple, la régression de la somme des carrés pour le premier élève est :

(ŷ _je – y ) ² = (71,69 – 81) ² = 86,64 .

Nous pouvons utiliser la même approche pour trouver la régression de la somme des carrés pour chaque élève :

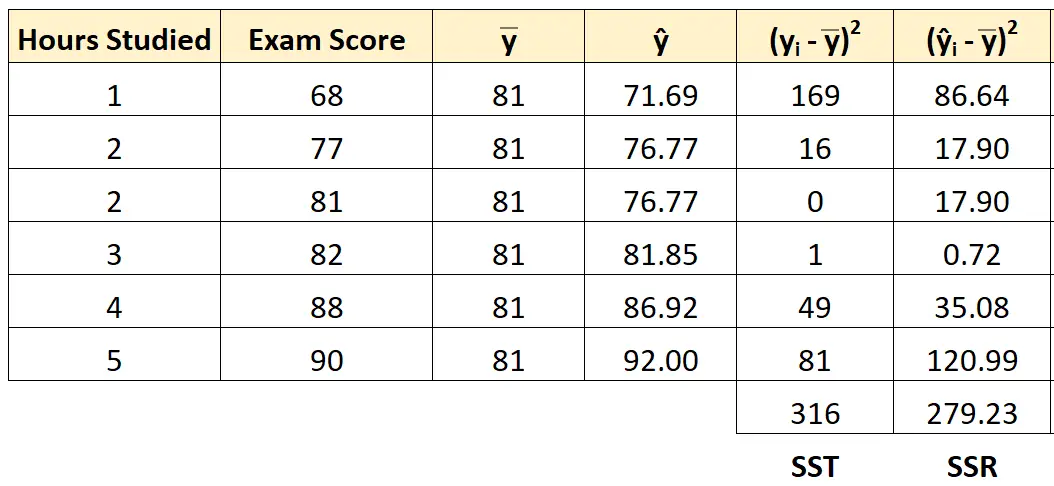
La régression de la somme des carrés s’avère être 279,23 .

Étape 5 : Calculez l’erreur de la somme des carrés (SSE).

Ensuite, nous pouvons calculer l’erreur de la somme des carrés.

Par exemple, l’erreur de somme des carrés pour le premier élève est :

(ŷ _je – y _je ) ² = (71,69 – 68) ² = 13,63 .

Nous pouvons utiliser la même approche pour trouver l’erreur de somme des carrés pour chaque élève :

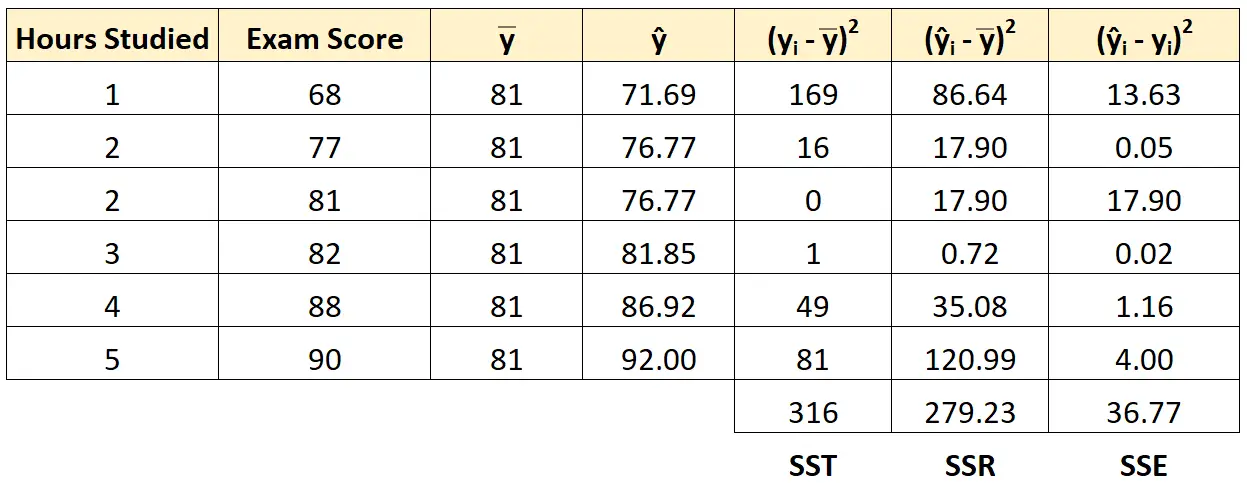
On peut vérifier que SST = SSR + SSE

• SST = SSR + SSE
• 316 = 279,23 + 36,77

Nous pouvons également calculer le R au carré du modèle de régression en utilisant l’équation suivante :

• R au carré = SSR / SST
• R au carré = 279,23 / 316
• R au carré = 0,8836

Cela nous indique que 88,36 % de la variation des résultats aux examens peut s’expliquer par le nombre d’heures étudiées.

Ressources additionnelles

Vous pouvez utiliser les calculatrices suivantes pour calculer automatiquement SST, SSR et SSE pour n’importe quelle ligne de régression linéaire simple :

Calculateur SST
Calculateur RSS
Calculateur ESS