Comment calculer SST, SSR et SSE dans Excel
Nous utilisons souvent trois valeurs de somme des carrés différentes pour mesurer dans quelle mesure une droite de régression s’adapte réellement à un ensemble de données :
1. Somme des carrés totaux (SST) – La somme des carrés des différences entre les points de données individuels (y i ) et la moyenne de la variable de réponse ( y ).
- SST = Σ(y je – y ) 2
2. Régression de la somme des carrés (SSR) – La somme des carrés des différences entre les points de données prédits (ŷ i ) et la moyenne de la variable de réponse ( y ).
- SSR = Σ(ŷ je – y ) 2
3. Erreur de somme des carrés (SSE) – La somme des carrés des différences entre les points de données prédits (ŷ i ) et les points de données observés (y i ).
- SSE = Σ(ŷ je – y je ) 2
L’exemple étape par étape suivant montre comment calculer chacune de ces métriques pour un modèle de régression donné dans Excel.
Étape 1 : Créer les données
Tout d’abord, créons un ensemble de données contenant le nombre d’heures étudiées et les résultats des examens obtenus pour 20 étudiants différents dans une école donnée :
Étape 2 : Ajuster un modèle de régression
Dans le ruban supérieur d’Excel, cliquez sur l’onglet Données et cliquez sur Analyse des données . Si vous ne voyez pas cette option, vous devez d’abord installer le logiciel gratuit Analysis ToolPak .

Une fois que vous avez cliqué sur Analyse des données, une nouvelle fenêtre apparaîtra. Sélectionnez Régression et cliquez sur OK.
Dans la nouvelle fenêtre qui apparaît, renseignez les informations suivantes :
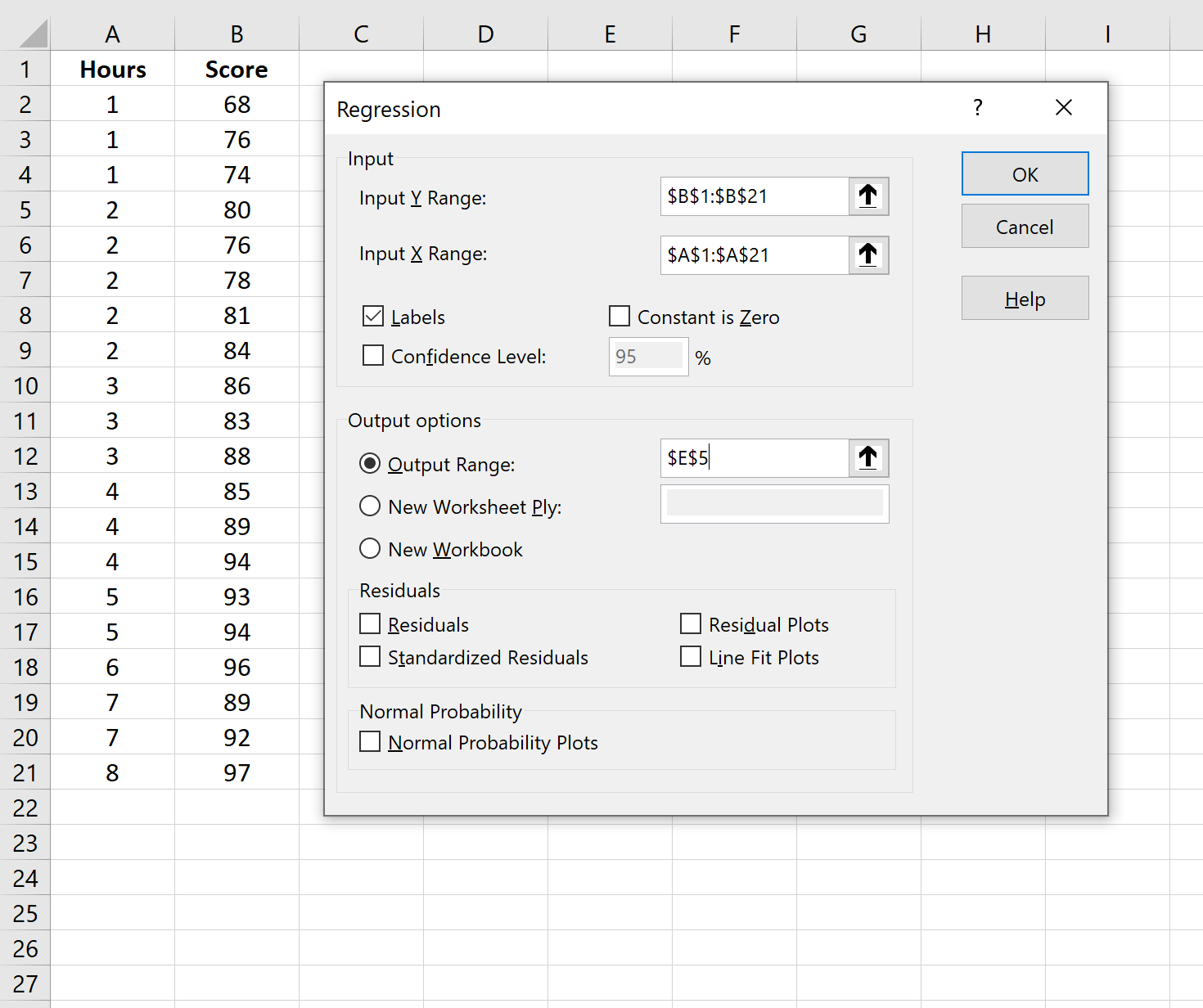
Une fois que vous avez cliqué sur OK , la sortie de régression apparaîtra.
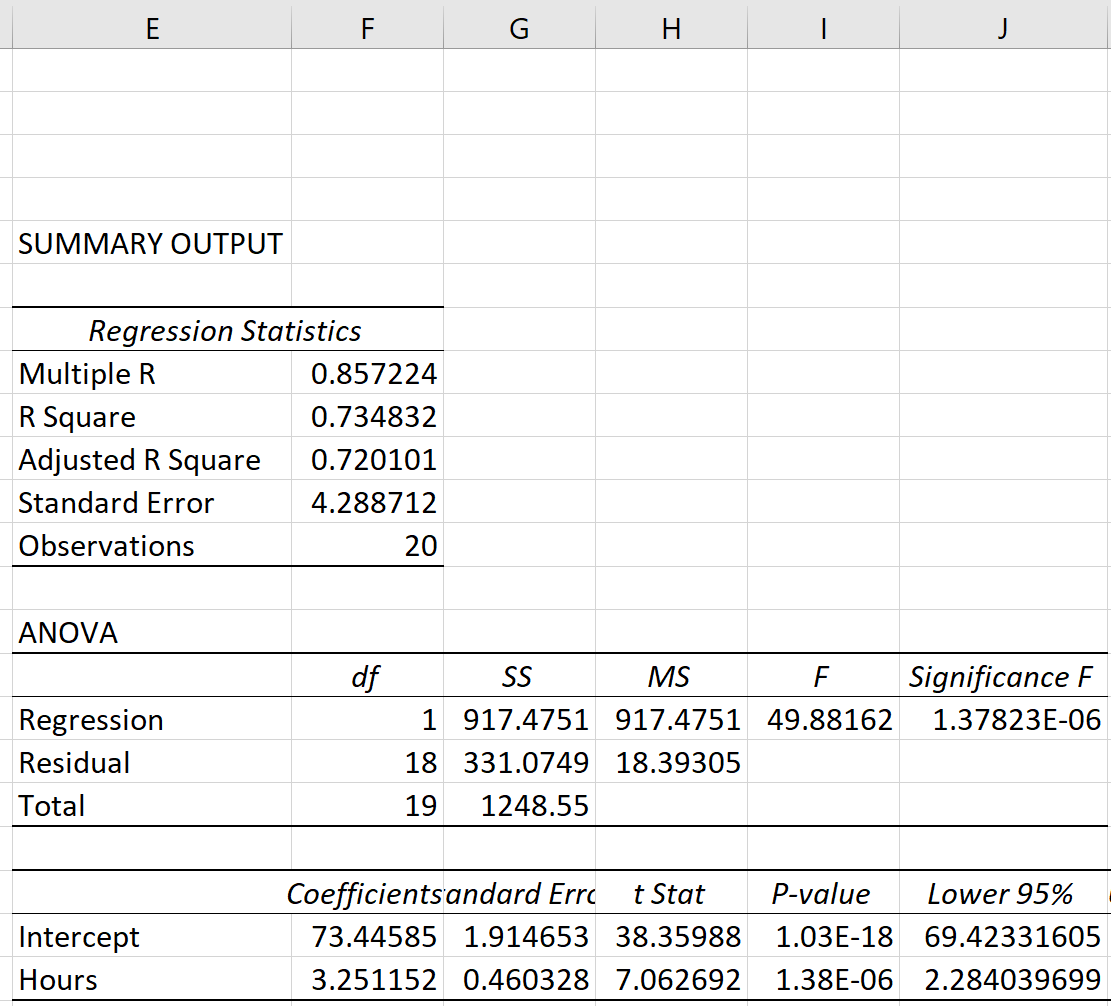
Étape 3 : Analyser le résultat
Les trois métriques de la somme des carrés – SST, SSR et SSE – peuvent être vues dans la colonne SS du tableau ANOVA :
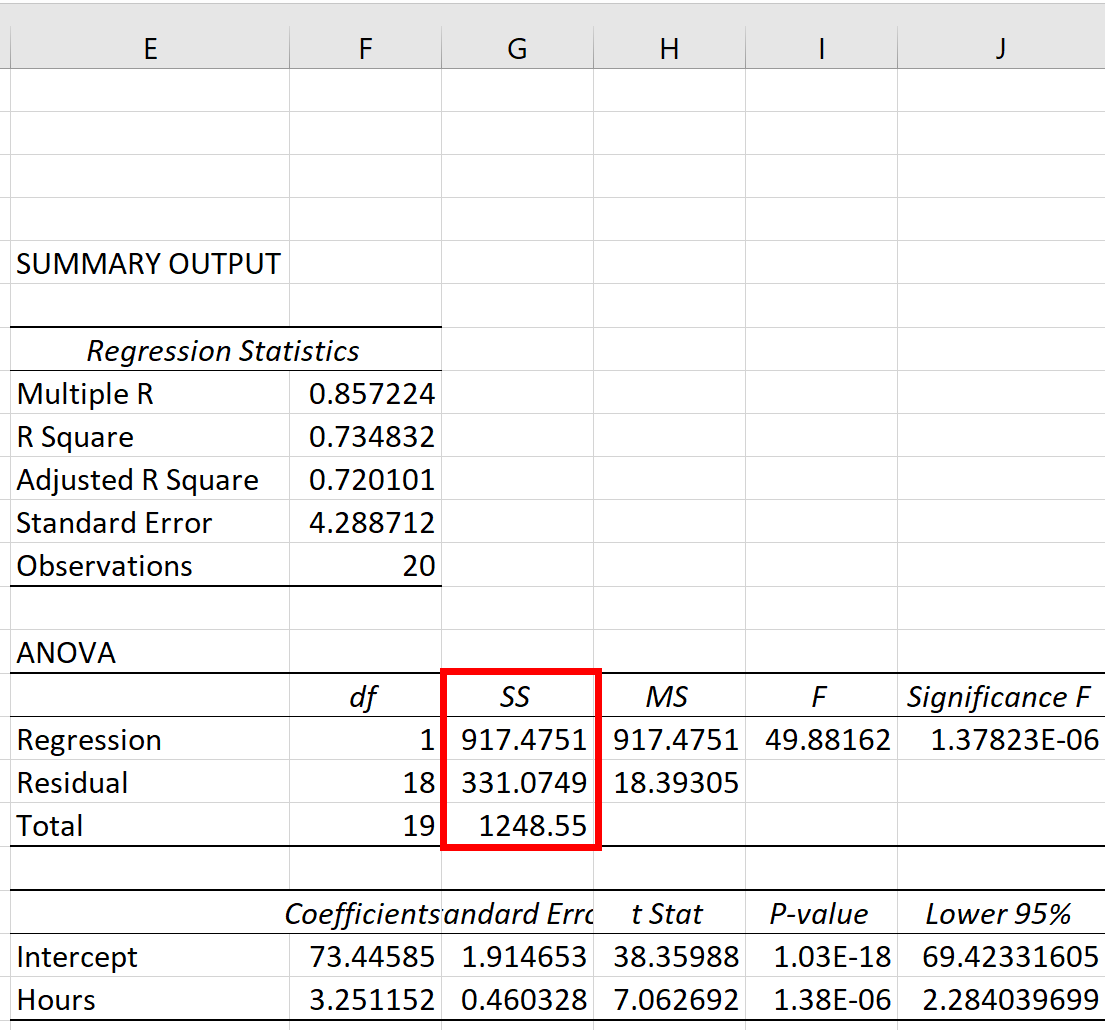
Les métriques s’avèrent être :
- Somme des carrés total (SST) : 1248,55
- Régression de la somme des carrés (SSR) : 917,4751
- Erreur de somme des carrés (SSE) : 331,0749
On peut vérifier que SST = SSR + SSE :
- SST = SSR + SSE
- 1248,55 = 917,4751 + 331,0749
Nous pouvons également calculer manuellement le R au carré du modèle de régression :
- R au carré = SSR / SST
- R au carré = 917,4751 / 1248,55
- R au carré = 0,7348
Cela nous indique que 73,48 % de la variation des résultats aux examens peut s’expliquer par le nombre d’heures étudiées.
Ressources additionnelles
Comment effectuer une régression linéaire simple dans Excel
Comment effectuer une régression linéaire multiple dans Excel
Comment effectuer une régression polynomiale dans Excel
Comment effectuer une régression exponentielle dans Excel
