Comment effectuer une régression quadratique dans Stata
Lorsque deux variables ont une relation linéaire, vous pouvez souvent utiliser une simple régression linéaire pour quantifier leur relation.

Cependant, lorsque deux variables ont une relation quadratique, vous pouvez utiliser la régression quadratique pour quantifier leur relation.

Ce tutoriel explique comment effectuer une régression quadratique dans Stata.
Exemple : régression quadratique dans Stata
Supposons que nous souhaitions comprendre la relation entre le nombre d’heures travaillées et le bonheur. Nous disposons des données suivantes sur le nombre d’heures travaillées par semaine et le niveau de bonheur déclaré (sur une échelle de 0 à 100) pour 16 personnes différentes :
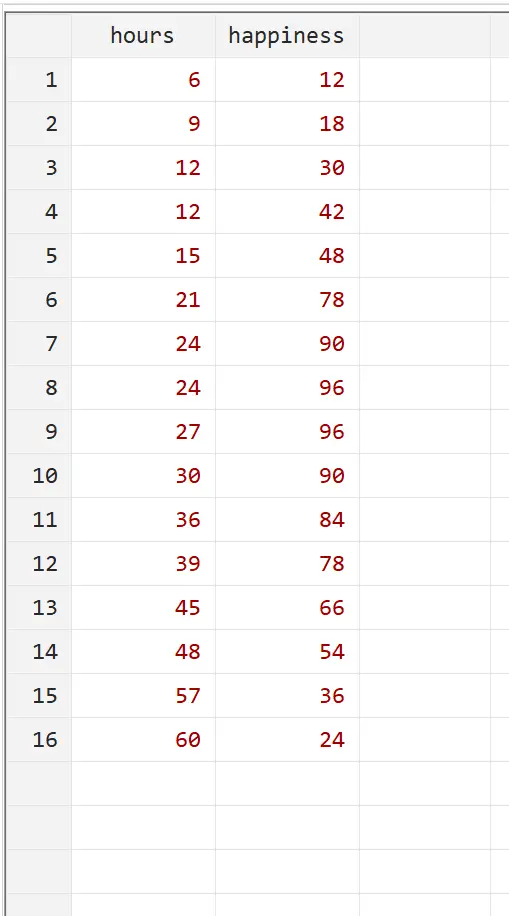
Vous pouvez reproduire cet exemple en saisissant ces données exactes dans Stata en utilisant Données > Éditeur de données > Éditeur de données (Modifier) dans le menu supérieur.
Utilisez les étapes suivantes pour effectuer une régression quadratique dans Stata.
Étape 1 : Visualisez les données.
Avant de pouvoir utiliser la régression quadratique, nous devons nous assurer que la relation entre la variable explicative (heures) et la variable de réponse (bonheur) est bien quadratique. Visualisons donc les données à l’aide d’un nuage de points en tapant ce qui suit dans la zone Commande :
disperser les heures de bonheur
Cela produit le nuage de points suivant :
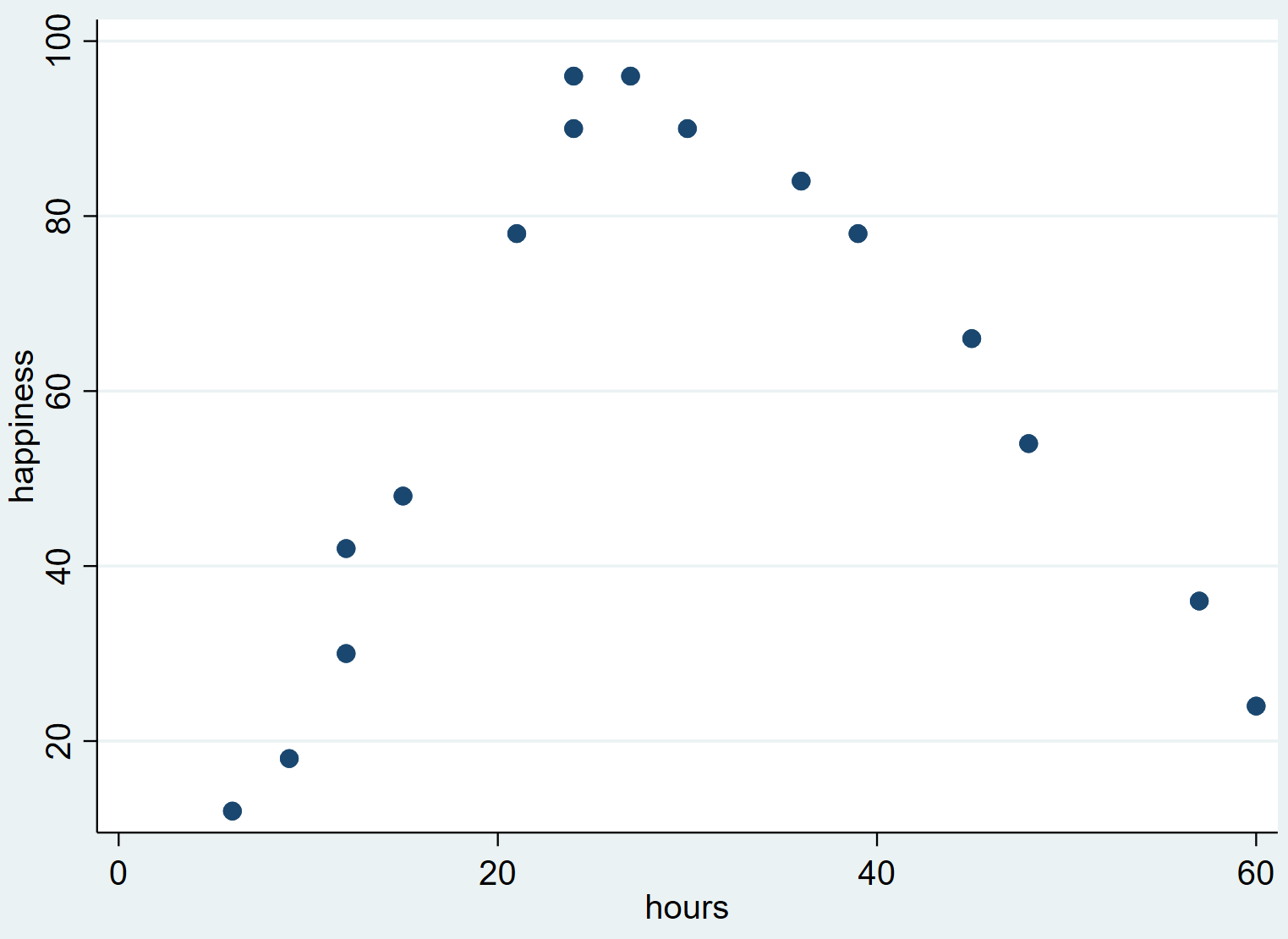
Nous pouvons voir que le bonheur a tendance à augmenter à mesure que le nombre d’heures travaillées augmente de zéro jusqu’à un certain point, mais commence ensuite à diminuer à mesure que le nombre d’heures travaillées dépasse environ 30.
Cette forme de « U » inversé dans le nuage de points indique qu’il existe une relation quadratique entre les heures travaillées et le bonheur, ce qui signifie que nous devrions utiliser la régression quadratique pour quantifier cette relation.
Étape 2 : Effectuez une régression quadratique.
Avant d’adapter le modèle de régression quadratique aux données, nous devons créer une nouvelle variable pour les valeurs au carré de notre variable prédictive hours . Nous pouvons le faire en tapant ce qui suit dans la zone Commande :
gen heures2 = heures*heures
Nous pouvons afficher cette nouvelle variable en accédant à Données > Éditeur de données > Éditeur de données (Parcourir) dans le menu supérieur.
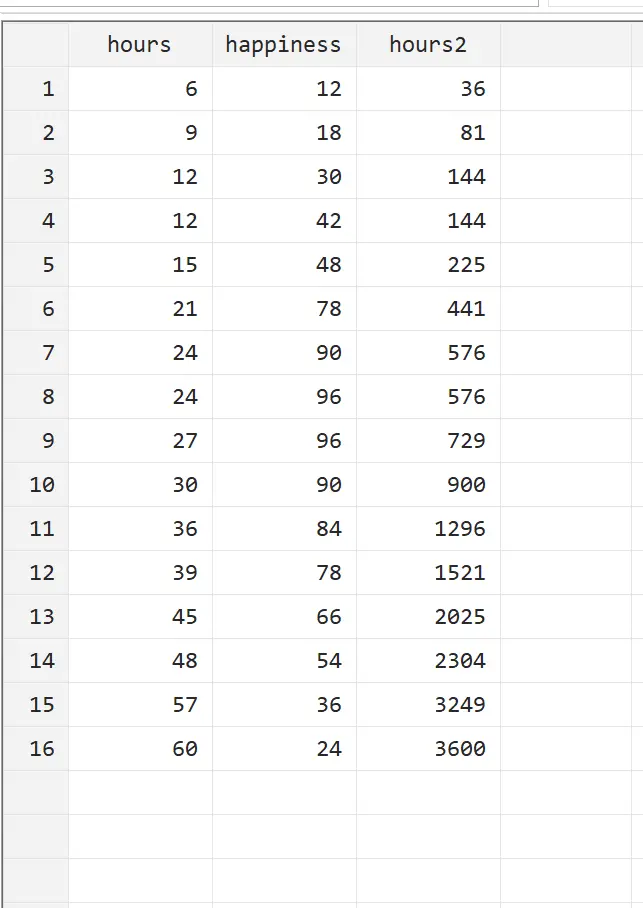
Nous pouvons voir que hours2 est simplement des heures au carré. Nous pouvons désormais effectuer une régression quadratique en utilisant les heures et les heures2 comme variables explicatives et le bonheur comme variable de réponse. Pour effectuer une régression quadratique, tapez ce qui suit dans la zone Commande :
régresser les heures de bonheur heures2
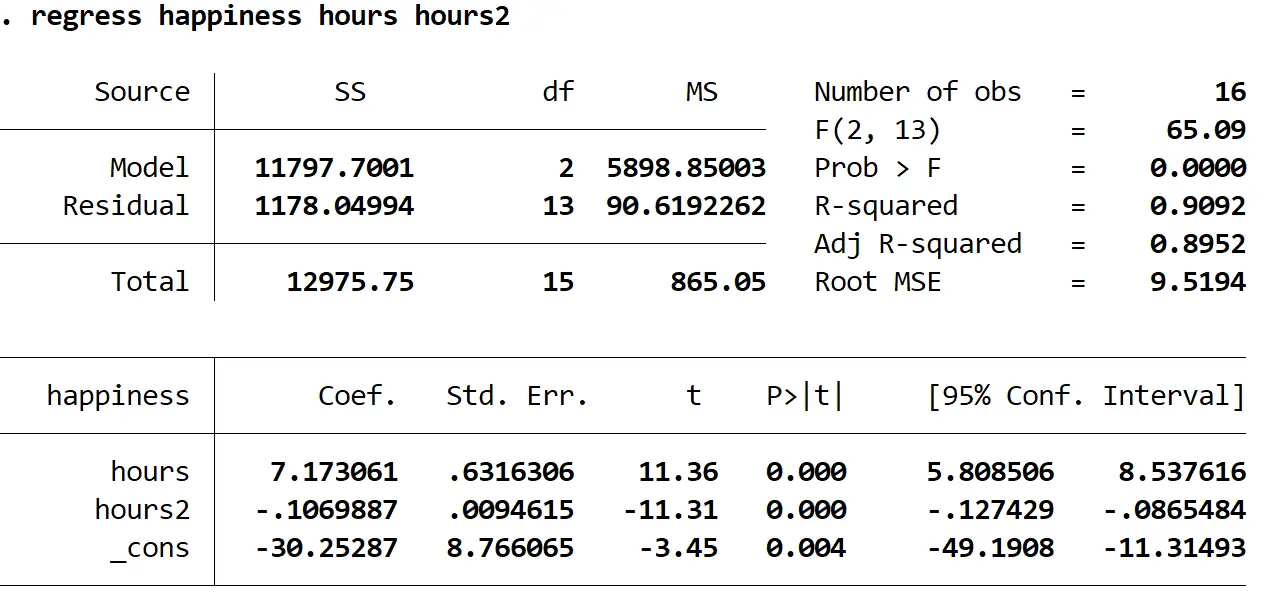
Voici comment interpréter les nombres les plus intéressants du résultat :
Prob > F : 0,000. Il s’agit de la valeur p pour la régression globale. Puisque cette valeur est inférieure à 0,05, cela signifie que les variables prédictives heures et heures 2 combinées ont une relation statistiquement significative avec la variable de réponse bonheur .
R au carré : 0,9092. Il s’agit de la proportion de la variance de la variable de réponse qui peut être expliquée par la variable explicative. Dans cet exemple, 90,92 % de la variation du bonheur peut s’expliquer par les heures et les heures 2 .
Équation de régression : nous pouvons former une équation de régression en utilisant les valeurs des coefficients indiquées dans le tableau de sortie. Dans ce cas, l’équation serait :
bonheur prédit = -30,25287 + 7,173061 (heures) – 0,1069887 (heures 2 )
Nous pouvons utiliser cette équation pour trouver le bonheur prédit d’un individu, compte tenu du nombre d’heures qu’il travaille par semaine.
Par exemple, une personne qui travaille 60 heures par semaine devrait avoir un niveau de bonheur de 14,97 :
bonheur prédit = -30,25287 + 7,173061(60) – .1069887(60 2 ) = 14,97 .
À l’inverse, une personne qui travaille 30 heures par semaine devrait avoir un niveau de bonheur de 88,65 :
bonheur prédit = -30,25287 + 7,173061(30) – .1069887(30 2 ) = 88,65 .
Étape 3 : Rapportez les résultats.
Enfin, nous souhaitons rapporter les résultats de notre régression quadratique. Voici un exemple de la façon de procéder :
Une régression quadratique a été réalisée pour quantifier la relation entre le nombre d’heures travaillées par un individu et son niveau de bonheur correspondant (mesuré de 0 à 100). Un échantillon de 16 personnes a été utilisé dans l’analyse.
Les résultats ont montré qu’il existait une relation statistiquement significative entre les variables explicatives heures et heures 2 et la variable de réponse bonheur (F(2, 13) = 65,09, p < 0,0001).
Ensemble, ces deux variables explicatives représentaient 90,92 % de la variabilité expliquée du bonheur.
L’équation de régression s’est avérée être :
bonheur prédit = -30,25287 + 7,173061 (heures) – 0,1069887 (heures 2 )
