Qu’est-ce qu’une statistique de test standardisé ?
Une hypothèse statistique est une hypothèse concernant un paramètre de population . Par exemple, nous pouvons supposer que la taille moyenne d’un homme aux États-Unis est de 70 pouces. L’hypothèse concernant la taille est l’ hypothèse statistique et la véritable taille moyenne d’un homme aux États-Unis est le paramètre de population .
Un test d’hypothèse est un test statistique formel que nous utilisons pour rejeter ou échouer à rejeter une hypothèse statistique.
Le processus de base pour effectuer un test d’hypothèse est le suivant :
1. Collectez des exemples de données.
2. Calculez la statistique de test standardisée pour les exemples de données.
3. Comparez la statistique du test standardisé à une valeur critique. Si c’est plus extrême que la valeur critique, rejetez l’hypothèse nulle. Sinon, ne rejetez pas le test de l’hypothèse nulle.
La formule que nous utilisons pour calculer la statistique du test standardisé varie en fonction du type de test d’hypothèse que nous effectuons.
Le tableau suivant présente la formule à utiliser pour calculer la statistique du test standardisé pour chacun des quatre principaux types de tests d’hypothèse :
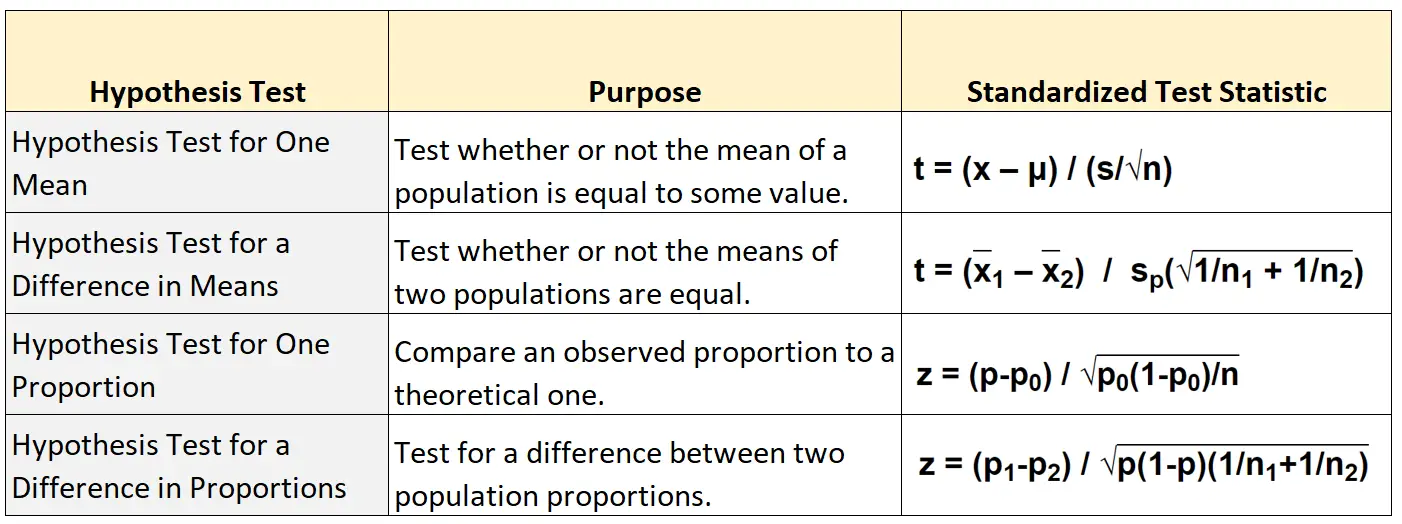
Test d’hypothèse pour une moyenne
Un test t sur un échantillon est utilisé pour tester si la moyenne d’une population est égale ou non à une certaine valeur.
La statistique de test standardisée pour ce type de test est calculée comme suit :
t = ( X – μ) / (s/√n)
où:
- x : moyenne de l’échantillon
- μ 0 : moyenne hypothétique de la population
- s : écart type de l’échantillon
- n : taille de l’échantillon
Reportez-vous à ce didacticiel pour un exemple de calcul de cette statistique de test standardisé.
Test d’hypothèse pour une différence de moyennes
Un test t à deux échantillons est utilisé pour tester si les moyennes de deux populations sont égales ou non.
La statistique de test standardisée pour ce type de test est calculée comme suit :
t = ( X 1 – X 2 ) / s p (√ 1/n 1 + 1/n 2 )
où x 1 et x 2 sont les moyennes de l’échantillon, n 1 et n 2 sont les tailles d’échantillon, et où s p est calculé comme suit :
s p = √ (n 1 -1)s 1 2 + (n 2 -1)s 2 2 / (n 1 +n 2 -2)
où s 1 2 et s 2 2 sont les variances de l’échantillon.
Reportez-vous à ce didacticiel pour un exemple de calcul de cette statistique de test standardisé.
Test d’hypothèse pour une proportion
Un test z à une proportion est utilisé pour comparer une proportion observée à une proportion théorique.
La statistique de test standardisée pour ce type de test est calculée comme suit :
z = (pp 0 ) / √ p 0 (1-p 0 )/n
où:
- p : proportion d’échantillon observée
- p 0 : proportion hypothétique de la population
- n : taille de l’échantillon
Reportez-vous àce didacticiel pour un exemple de calcul de cette statistique de test standardisé.
Test d’hypothèse pour une différence de proportions
Un test z à deux proportions est utilisé pour tester une différence entre deux proportions de population.
La statistique de test standardisée pour ce type de test est calculée comme suit :
z = (p 1 -p 2 ) / √ p(1-p)(1/n 1 +1/n 2 )
où p 1 et p 2 sont les proportions de l’échantillon, n 1 et n 2 sont les tailles d’échantillon, et où p est la proportion totale regroupée calculée comme suit :
p = (p 1 n 1 + p 2 n 2 )/(n 1 + n 2 )
Reportez-vous à ce didacticiel pour un exemple de calcul de cette statistique de test standardisé.
à propos de l'auteur
Dr. Benjamin Anderson
Il est un professeur de statistiques à la retraite devenu éducateur dévoué sur Statorials. Avec une vaste expérience et une expertise dans le domaine des statistiques, je m'engage à partager mes connaissances pour responsabiliser les étudiants grâce à Statorials. Lire plus