Qu’est-ce que l’erreur de prédiction dans les statistiques ? (Définition & Exemples)

En statistiques, l’erreur de prédiction fait référence à la différence entre les valeurs prédites par certains modèles et les valeurs réelles.

L’erreur de prédiction est souvent utilisée dans deux contextes :

1. Régression linéaire : utilisée pour prédire la valeur d’une variable à réponse continue.

Nous mesurons généralement l’erreur de prédiction d’un modèle de régression linéaire avec une métrique connue sous le nom de RMSE , qui signifie erreur quadratique moyenne.

Il est calculé comme suit :

RMSE = √ Σ(ŷ _je – y _je ) ² / n

où:

• Σ est un symbole qui signifie « somme »
• ŷ _i est la valeur prédite pour la i ^ème observation
• y _i est la valeur observée pour la ^ième observation
• n est la taille de l’échantillon

2. Régression logistique : utilisée pour prédire la valeur d’une variable de réponse binaire.

Une façon courante de mesurer l’erreur de prédiction d’un modèle de régression logistique consiste à utiliser une mesure connue sous le nom de taux total d’erreurs de classification.

Il est calculé comme suit :

Taux total d’erreurs de classification = (# prédictions incorrectes / # prédictions totales)

Plus la valeur du taux de classification erronée est faible, plus le modèle est capable de prédire les résultats de la variable de réponse.

Les exemples suivants montrent comment calculer l’erreur de prédiction pour un modèle de régression linéaire et un modèle de régression logistique dans la pratique.

Exemple 1 : Calcul de l’erreur de prédiction dans la régression linéaire

Supposons que nous utilisions un modèle de régression pour prédire le nombre de points que 10 joueurs marqueront dans un match de basket-ball.

Le tableau suivant montre les points prédits par le modèle par rapport aux points réels marqués par les joueurs :

Nous calculerions l’erreur quadratique moyenne (RMSE) comme suit :

• RMSE = √ Σ(ŷ _je – y _je ) ² / n
• RMSE = √(((14-12) ² +(15-15) ² +(18-20) ² +(19-16) ² +(25-20) ² +(18-19) ² +(12- 16) ² +(12-20) ² +(15-16) ² +(22-16) ² ) / 10)
• RMSE = 4

L’erreur quadratique moyenne est de 4. Cela nous indique que l’écart moyen entre les points marqués prédits et les points réels marqués est de 4.

Connexe : Qu’est-ce qui est considéré comme une bonne valeur RMSE ?

Exemple 2 : Calcul de l’erreur de prédiction dans la régression logistique

Supposons que nous utilisions un modèle de régression logistique pour prédire si 10 joueurs de basket-ball universitaires seront recrutés ou non dans la NBA.

Le tableau suivant montre le résultat prévu pour chaque joueur par rapport au résultat réel (1 = repêché, 0 = non repêché) :

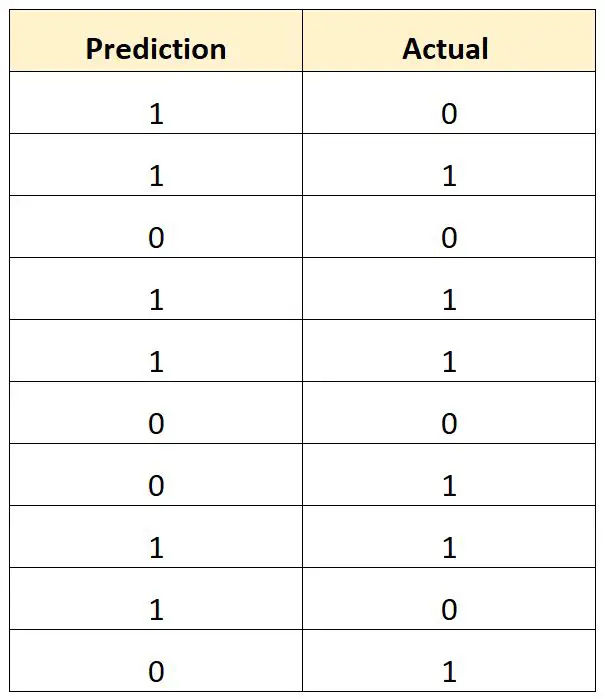
Nous calculerions le taux total d’erreurs de classification comme suit :

• Taux total d’erreurs de classification = (# prédictions incorrectes / # prédictions totales)
• Taux total d’erreurs de classification = 4/10
• Taux total d’erreurs de classification = 40 %

Le taux total d’erreurs de classification est de 40 % .

Cette valeur est assez élevée, ce qui indique que le modèle ne fait pas un très bon travail pour prédire si un joueur sera repêché ou non.

Ressources additionnelles

Les didacticiels suivants fournissent une introduction aux différents types de méthodes de régression :

Introduction à la régression linéaire simple
Introduction à la régression linéaire multiple
Introduction à la régression logistique