Qu’est-ce qu’une fonction de masse de probabilité (PMF) en statistique ?

Une fonction de masse de probabilité , souvent abrégée PMF , nous indique la probabilité qu’une variable aléatoire discrète prenne une certaine valeur.

Par exemple, supposons que nous lançons un dé une fois. Si nous laissons x désigner le nombre sur lequel le dé tombe, alors la probabilité que x soit égal à différentes valeurs peut être décrite comme suit :

• P(X=1) : 1/6
• P(X=2) : 1/6
• P(X=3) : 1/6
• P(X=4) : 1/6
• P(X=5) : 1/6
• P(X=6) : 1/6

Il y a une chance égale que les dés tombent sur n’importe quel nombre compris entre 1 et 6.

Voici comment nous écririons ces probabilités sous forme de fonction de masse de probabilité :

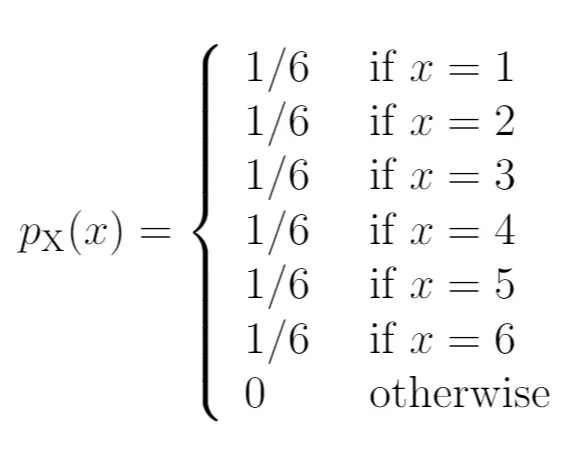
Le côté gauche du diagramme montre la probabilité associée aux résultats du côté droit :

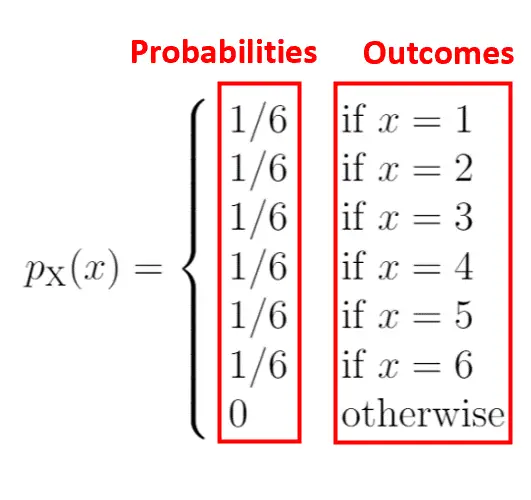
Une caractéristique d’une fonction de masse de probabilité est que toutes les probabilités doivent totaliser 1. Vous remarquerez que ce PMF satisfait à cette condition :

Somme des probabilités = 1/6 + 1/6 + 1/6 + 1/6 + 1/6 + 1/6 = 1.

La prise en charge d’une fonction de masse de probabilité fait référence à l’ensemble de valeurs que la variable aléatoire discrète peut prendre. Dans cet exemple, le support serait {1, 2, 3, 4, 5, 6} puisque la valeur du dé peut prendre n’importe laquelle de ces valeurs.

En dehors du support, la valeur du PMF est égale à zéro. Par exemple, la probabilité que le dé tombe sur « 0 » ou « 7 » ou « 8 » est égale à zéro puisqu’aucun de ces nombres n’est inclus dans le support.

Fonctions de masse de probabilité en pratique

Les deux exemples les plus courants de fonctions de masse de probabilité dans la pratique concernent la distribution binomiale et la distribution de Poisson .

Distribution binomiale

Si une variable aléatoire X suit une distribution binomiale, alors la probabilité que X = k succès peut être trouvée par la formule suivante :

P(X=k) = _n C _k * p ^k * (1-p) ^nk

où:

• n : nombre d’essais
• k : nombre de réussites
• p : probabilité de succès sur un essai donné
• _n C _k : le nombre de façons d’obtenir k succès dans n essais

Par exemple, supposons que nous lançons une pièce 3 fois. Nous pouvons utiliser la formule ci-dessus pour déterminer la probabilité d’obtenir 0, 1, 2 et 3 face lors de ces 3 lancers :

• P(X=0) = ₃ C ₀ * 0,5 ⁰ * (1-0,5) ^3-0 = 1 * 1 * (0,5) ³ = 0,125
• P(X=1) = ₃ C ₁ * 0,5 ¹ * (1-0,5) ^3-1 = 1 * 1 * (0,5) ² = 0,375
• P(X=2) = ₃ C ₂ * 0,5 ² * (1-0,5) ^3-2 = 1 * 1 * (0,5) ¹ = 0,375
• P(X=3) = ₃ C ₃ * 0,5 ³ * (1-0,5) ^3-3 = 1 * 1 * (0,5) ⁰ = 0,125

Distribution de Poisson

Si une variable aléatoire X suit une distribution de Poisson, alors la probabilité que X = k succès peut être trouvée par la formule suivante :

P(X=k) = λ ^k * e ^{– λ} / k !

où:

• λ : nombre moyen de succès survenus au cours d’un intervalle spécifique
• k : nombre de réussites
• e : une constante égale à environ 2,71828

Par exemple, supposons qu’un hôpital particulier connaisse en moyenne 2 naissances par heure. Nous pouvons utiliser la formule ci-dessus pour déterminer la probabilité de connaître 0, 1, 2, 3 naissances, etc. dans une heure donnée :

• P(X=0) = 2 ⁰ * e ^{– 2} / 0 ! = 0,1353
• P(X=1) = 2 ¹ * e ^{– 2} / 1 ! = 0,2707
• P(X=2) = 2 ² * e ^{– 2} / 2 ! = 0,2707
• P(X=3) = 2 ³ * e ^{– 2} / 3 ! = 0,1805

Visualiser un PMF

Nous visualisons souvent les fonctions de masse de probabilité avec des graphiques à barres.

Par exemple, le graphique à barres suivant montre les probabilités associées au nombre de naissances par heure pour la distribution de Poisson décrite dans l’exemple précédent :

Notez que le nombre de naissances pourrait s’étendre à l’infini, mais les probabilités deviennent si faibles après 10 qu’on ne peut même pas les voir sur un graphique à barres.

Propriétés d’un PMF

Une fonction de masse de probabilité a les propriétés suivantes :

1. Toutes les probabilités sont positives dans le support. Par exemple, la probabilité qu’un dé tombe entre 1 et 6 est positive, tandis que la probabilité de tous les autres résultats est égale à zéro.

2. Tous les résultats ont une probabilité comprise entre 0 et 1. Par exemple, la probabilité qu’un dé tombe entre 1 et 6 est de 1/6, soit 0,1666666 pour chaque résultat.

3. La somme de toutes les probabilités doit être égale à 1. Par exemple, la somme des probabilités qu’un dé tombe sur un certain nombre est 1/6 + 1/6 + 1/6 + 1/6 + 1/6 + 1. /6 = 1.

Ressources additionnelles

Que sont les variables aléatoires ?
CDF ou PDF : quelle est la différence ?
Une introduction à la distribution binomiale
Une introduction à la distribution de Poisson