Parcelles à tiges et feuilles : comment trouver la moyenne, la médiane, & Mode
Un tracé à tiges et feuilles est un type de tracé qui affiche les données en divisant chaque valeur d’un ensemble de données en une tige et une feuille .
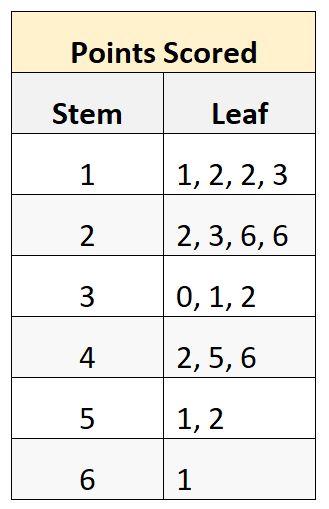
Ce didacticiel explique comment calculer la moyenne, la médiane et le mode d’un tracé à tiges et feuilles.
Exemple : moyenne, médiane et mode du tracé à tiges et à feuilles
Supposons que nous ayons le diagramme à tiges et feuilles suivant qui montre la hauteur de 19 plantes différentes :
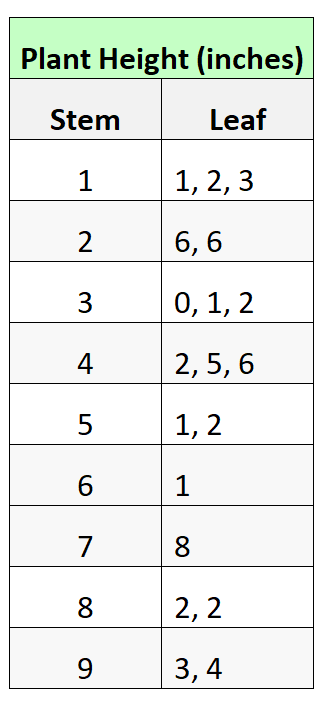
Signifier:
Pour trouver la moyenne de cet ensemble de données, nous pouvons additionner toutes les valeurs individuelles et diviser par la taille totale de l’échantillon de 19 :
Moyenne = (11+12+13+26+26+30+31+31+42+45+46+51+52+61+78+82+82+93+94) / 19 = 47,68 .
La moyenne s’avère être de 47,68 . Il s’agit de la valeur moyenne de l’ensemble de données.
Médian:
Pour trouver la médiane de cet ensemble de données, nous pouvons écrire toutes les valeurs individuelles dans l’ordre et identifier la valeur qui se situe directement au milieu :
11, 12, 13, 26, 26, 30, 31, 31, 42, 45 , 46, 51, 52, 61, 78, 82, 82, 93, 94
La médiane s’avère être de 45 . Il s’agit de la valeur située directement au milieu de l’ensemble de données.
Mode:
Pour trouver le mode de cet ensemble de données, nous pouvons identifier les valeurs qui apparaissent le plus souvent :
11, 12, 13, 26 , 26 , 30, 31, 31, 42, 45, 46, 51, 52, 61, 78, 82 , 82 , 93, 94
Cet ensemble de données a deux modes : 26 et 82 . Chacune de ces valeurs apparaît deux fois dans l’ensemble de données alors que toutes les autres valeurs n’apparaissent qu’une seule fois.
Ressources additionnelles
Générateur de parcelles de tiges et de feuilles
Comment créer un tracé à tiges et feuilles dans Excel
Comment créer des tracés à tiges et à feuilles dos à dos
Comment créer un tracé de tiges et de feuilles avec des décimales
