Qu’est-ce que le surapprentissage dans l’apprentissage automatique ? (Explication & Exemples)

Dans le domaine de l’apprentissage automatique, nous construisons souvent des modèles afin de pouvoir faire des prédictions précises sur certains phénomènes.

Par exemple, supposons que nous souhaitions créer un modèle de régression qui utilise la variable prédictive heures passées à étudier pour prédire le score ACT de la variable de réponse pour les élèves du secondaire.

Pour construire ce modèle, nous collecterons des données sur les heures passées à étudier et le score ACT correspondant pour des centaines d’élèves dans un certain district scolaire.

Nous utiliserons ensuite ces données pour former un modèle capable de faire des prédictions sur le score qu’un élève donné recevra en fonction du nombre total d’heures étudiées.

Pour évaluer l’utilité du modèle, nous pouvons mesurer dans quelle mesure les prédictions du modèle correspondent aux données observées. L’une des mesures les plus couramment utilisées pour ce faire est l’erreur quadratique moyenne (MSE), qui est calculée comme suit :

MSE = (1/n)*Σ(y _je – f(x _je )) ²

où:

• n : nombre total d’observations
• y _i : La valeur de réponse de la ^ième observation
• f(x _i ) : La valeur de réponse prédite de la i ^ème observation

Plus les prédictions du modèle sont proches des observations, plus la MSE sera faible.

Cependant, l’une des plus grandes erreurs commises dans l’apprentissage automatique est d’optimiser les modèles pour réduire le MSE d’entraînement , c’est-à-dire dans quelle mesure les prédictions du modèle correspondent aux données que nous avons utilisées pour entraîner le modèle.

Lorsqu’un modèle se concentre trop sur la réduction du MSE d’entraînement, il travaille souvent trop dur pour trouver des modèles dans les données d’entraînement qui sont simplement causés par le hasard. Ensuite, lorsque le modèle est appliqué à des données invisibles, ses performances sont médiocres.

Ce phénomène est connu sous le nom de surapprentissage . Cela se produit lorsque nous « ajustons » un modèle de trop près aux données d’entraînement et que nous finissons ainsi par construire un modèle qui n’est pas utile pour faire des prédictions sur de nouvelles données.

Exemple de surajustement

Pour comprendre le surapprentissage, revenons à l’exemple de création d’un modèle de régression qui utilise les heures passées à étudier pour prédire le score ACT .

Supposons que nous rassemblions des données pour 100 élèves dans un certain district scolaire et créions un nuage de points rapide pour visualiser la relation entre les deux variables :

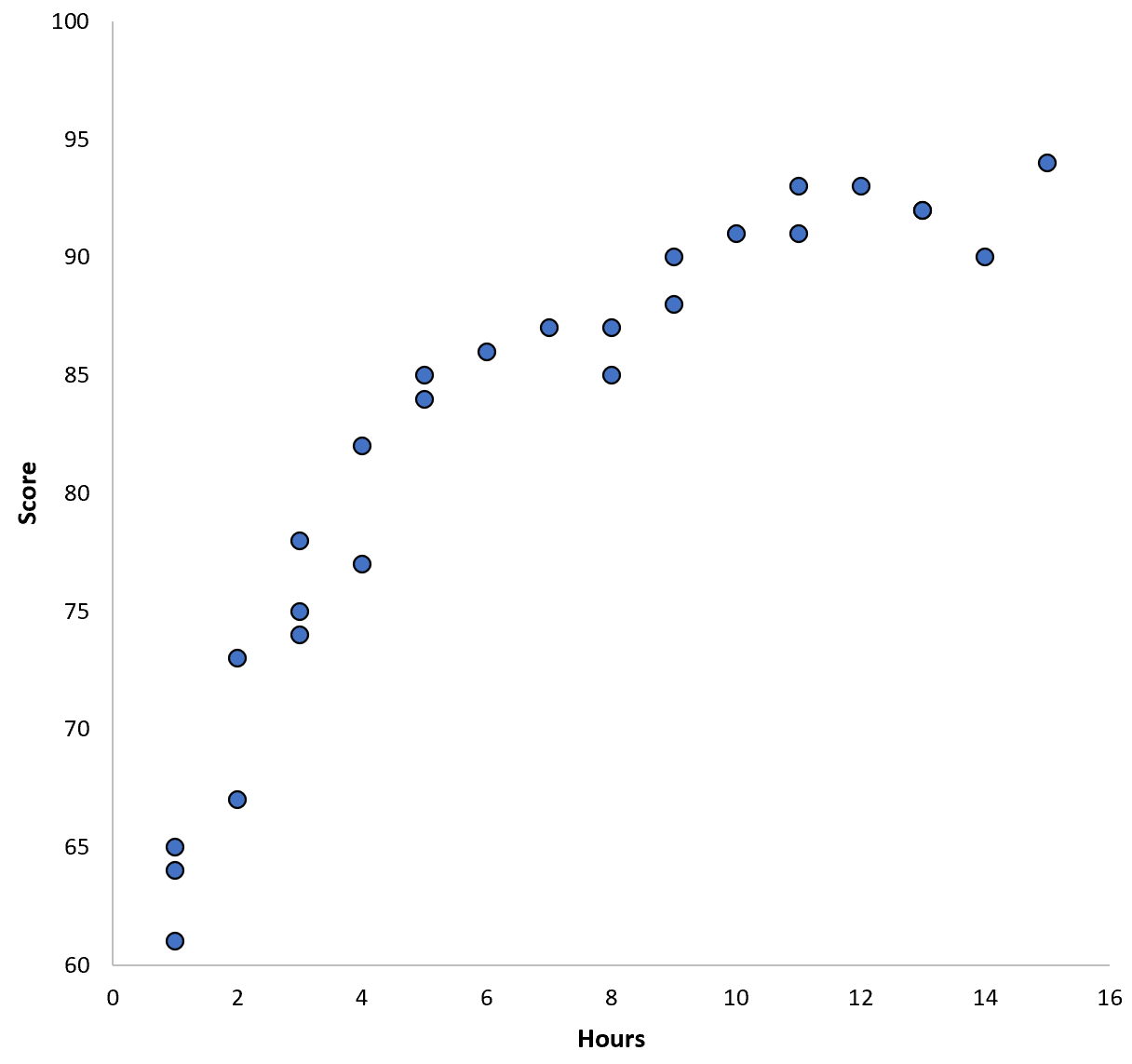
La relation entre les deux variables semble être quadratique, supposons donc que nous appliquions le modèle de régression quadratique suivant :

Score = 60,1 + 5,4*(Heures) – 0,2*(Heures) ²

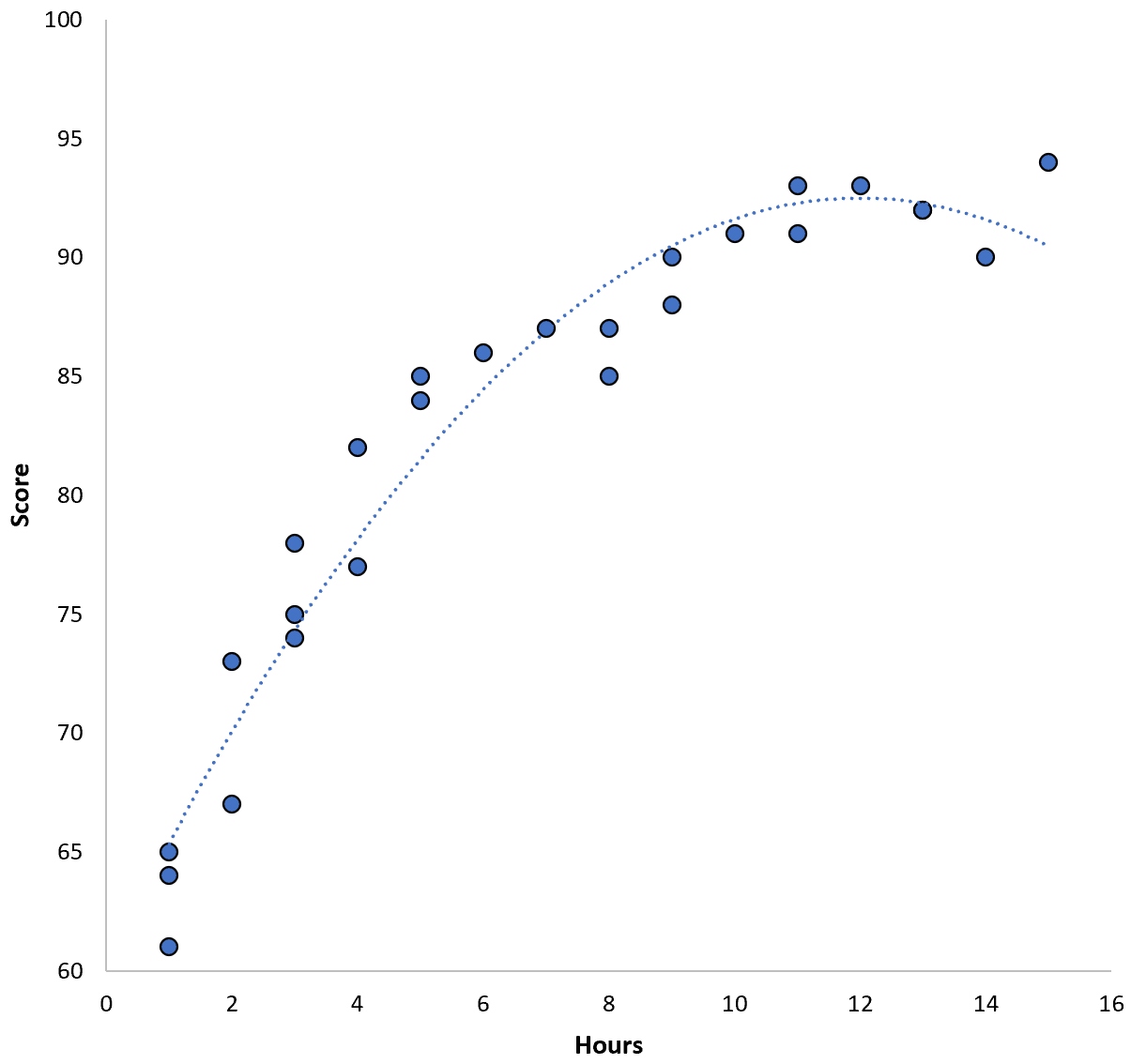
Ce modèle a une erreur quadratique moyenne (MSE) de formation de 3,45 . Autrement dit, la différence quadratique moyenne entre les prédictions faites par le modèle et les scores ACT réels est de 3,45.

Cependant, nous pourrions réduire cette MSE de formation en ajustant un modèle polynomial d’ordre supérieur. Par exemple, supposons que nous appliquions le modèle suivant :

Score = 64,3 – 7,1*(Heures) + 8,1*(Heures) ² – 2,1*(Heures) ³ + 0,2*(Heures) ⁴ – 0,1*(Heures) ⁵ + 0,2(Heures) ⁶

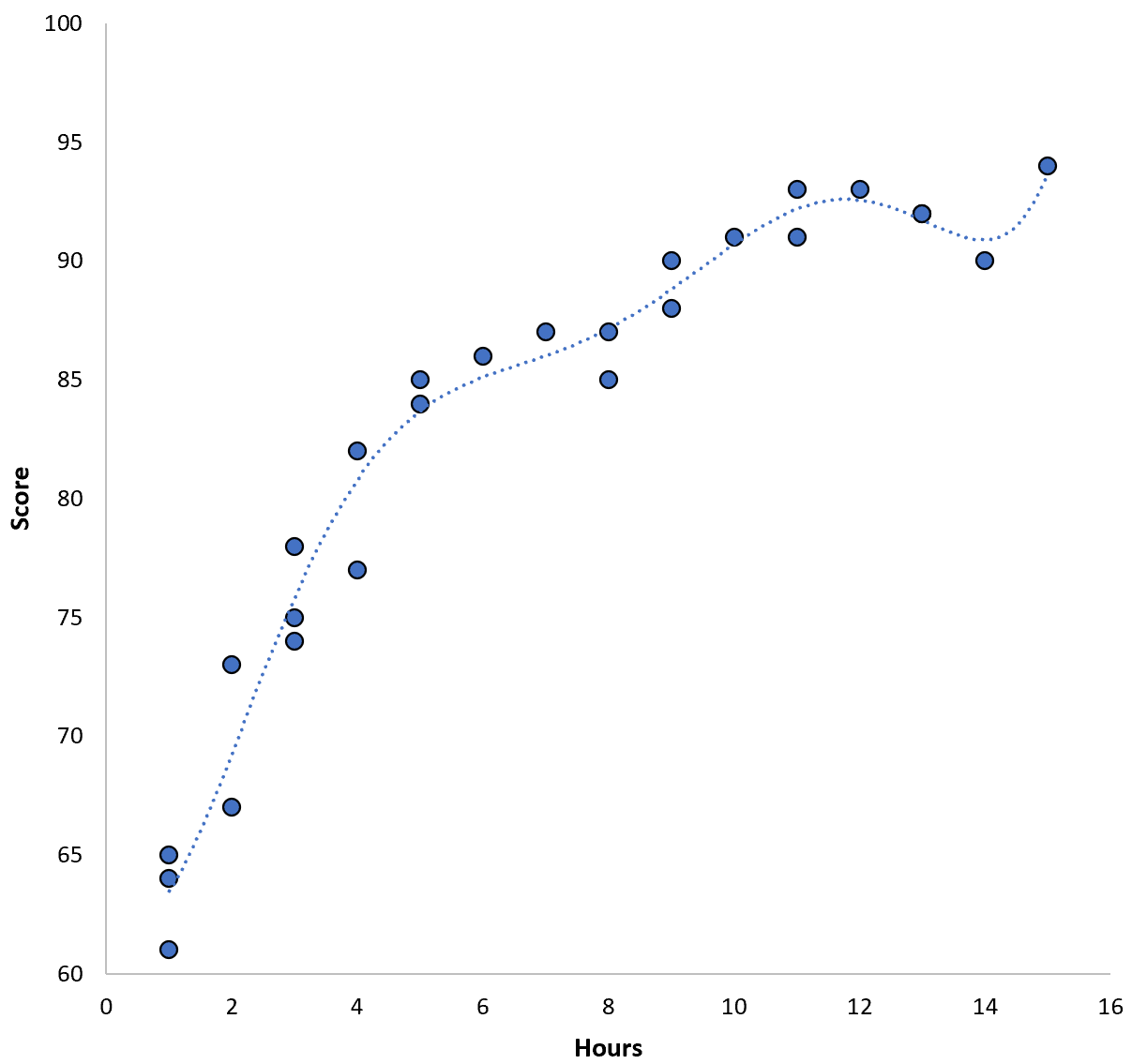
Remarquez comment la droite de régression épouse beaucoup plus étroitement les données réelles que la droite de régression précédente.

Ce modèle a une erreur quadratique moyenne (MSE) d’entraînement de seulement 0,89 . Autrement dit, la différence quadratique moyenne entre les prédictions faites par le modèle et les scores ACT réels est de 0,89.

Ce MSE de formation est beaucoup plus petit que celui produit par le modèle précédent.

Cependant, nous ne nous soucions pas vraiment du MSE d’entraînement , c’est-à-dire de la mesure dans laquelle les prédictions du modèle correspondent aux données que nous avons utilisées pour entraîner le modèle. Au lieu de cela, nous nous soucions principalement du test MSE – le MSE lorsque notre modèle est appliqué à des données invisibles.

Si nous appliquions le modèle de régression polynomiale d’ordre supérieur ci-dessus à un ensemble de données invisible, il serait probablement moins performant que le modèle de régression quadratique plus simple. Autrement dit, cela produirait un MSE de test plus élevé, ce qui est exactement ce que nous ne voulons pas.

Comment détecter et éviter le surapprentissage

Le moyen le plus simple de détecter le surapprentissage consiste à effectuer une validation croisée. La méthode la plus couramment utilisée est connue sous le nom de validation croisée k-fold et elle fonctionne comme suit :

Étape 1 : Divisez aléatoirement un ensemble de données en k groupes, ou « plis », de taille à peu près égale.

Étape 2 : Choisissez l’un des plis comme ensemble de maintien. Ajustez le modèle sur les plis k-1 restants. Calculez le test MSE sur les observations dans le pli qui a été tendu.

Étape 3 : Répétez ce processus k fois, en utilisant à chaque fois un ensemble différent comme ensemble d’exclusion.

Étape 4 : Calculez le MSE global du test comme étant la moyenne des k MSE du test.

Test MSE = (1/k)*ΣMSE _i

où:

• k : Nombre de plis
• MSE _i : Tester MSE à la ^ième itération

Ce test MSE nous donne une bonne idée de la façon dont un modèle donné fonctionnera sur des données invisibles.

En pratique, nous pouvons ajuster plusieurs modèles différents et effectuer une validation croisée k fois sur chaque modèle pour connaître son MSE de test. Nous pouvons ensuite choisir le modèle avec le MSE de test le plus bas comme meilleur modèle à utiliser pour faire des prédictions dans le futur.

Cela garantit que nous sélectionnons un modèle susceptible de fonctionner le mieux sur les données futures, par opposition à un modèle qui minimise simplement le MSE de formation et « s’adapte » bien aux données historiques.

Ressources additionnelles

Quel est le compromis biais-variance dans l’apprentissage automatique ?
Une introduction à la validation croisée K-Fold
Modèles de régression et de classification dans l’apprentissage automatique