Comment effectuer un test t de corrélation

Un coefficient de corrélation de Pearson est utilisé pour quantifier l’association linéaire entre deux variables.

Il prend toujours une valeur comprise entre -1 et 1 où :

• -1 indique une corrélation linéaire parfaitement négative.
• 0 indique aucune corrélation linéaire.
• 1 indique une corrélation linéaire parfaitement positive.

Pour déterminer si un coefficient de corrélation est statistiquement significatif, vous pouvez effectuer un test t, qui consiste à calculer un score t et une valeur p correspondante.

La formule pour calculer le t-score est la suivante :

t = r√ (n-2) / (1-r ² )

où:

• r : Le coefficient de corrélation
• n : La taille de l’échantillon

La valeur p est calculée comme la valeur p bilatérale correspondante pour la distribution t avec n-2 degrés de liberté.

L’exemple suivant montre comment effectuer un test t pour un coefficient de corrélation.

Exemple : exécution d’un test t pour la corrélation

Supposons que nous ayons l’ensemble de données suivant avec deux variables :

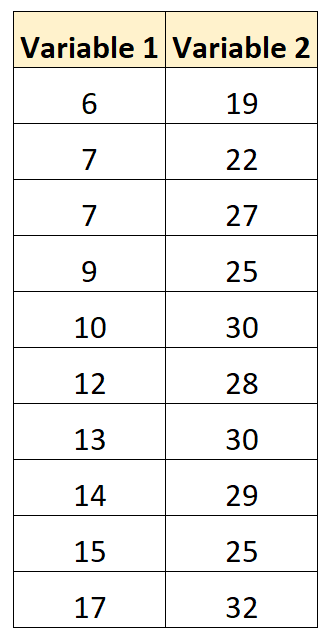
À l’aide de certains logiciels statistiques (Excel, R, Python, etc.), nous pouvons calculer le coefficient de corrélation entre les deux variables à 0,707 .

Il s’agit d’une corrélation très positive, mais pour déterminer si elle est statistiquement significative, nous devons calculer le score t et la valeur p correspondants.

Nous pouvons calculer le t-score comme suit :

• t = r√ (n-2) / (1-r ² )
• t = 0,707√ (10-2) / (1-0,707 ² )
• t = 2,828

À l’aide d’un calculateur de score T à valeur P , nous constatons que la valeur p correspondante est de 0,022 .

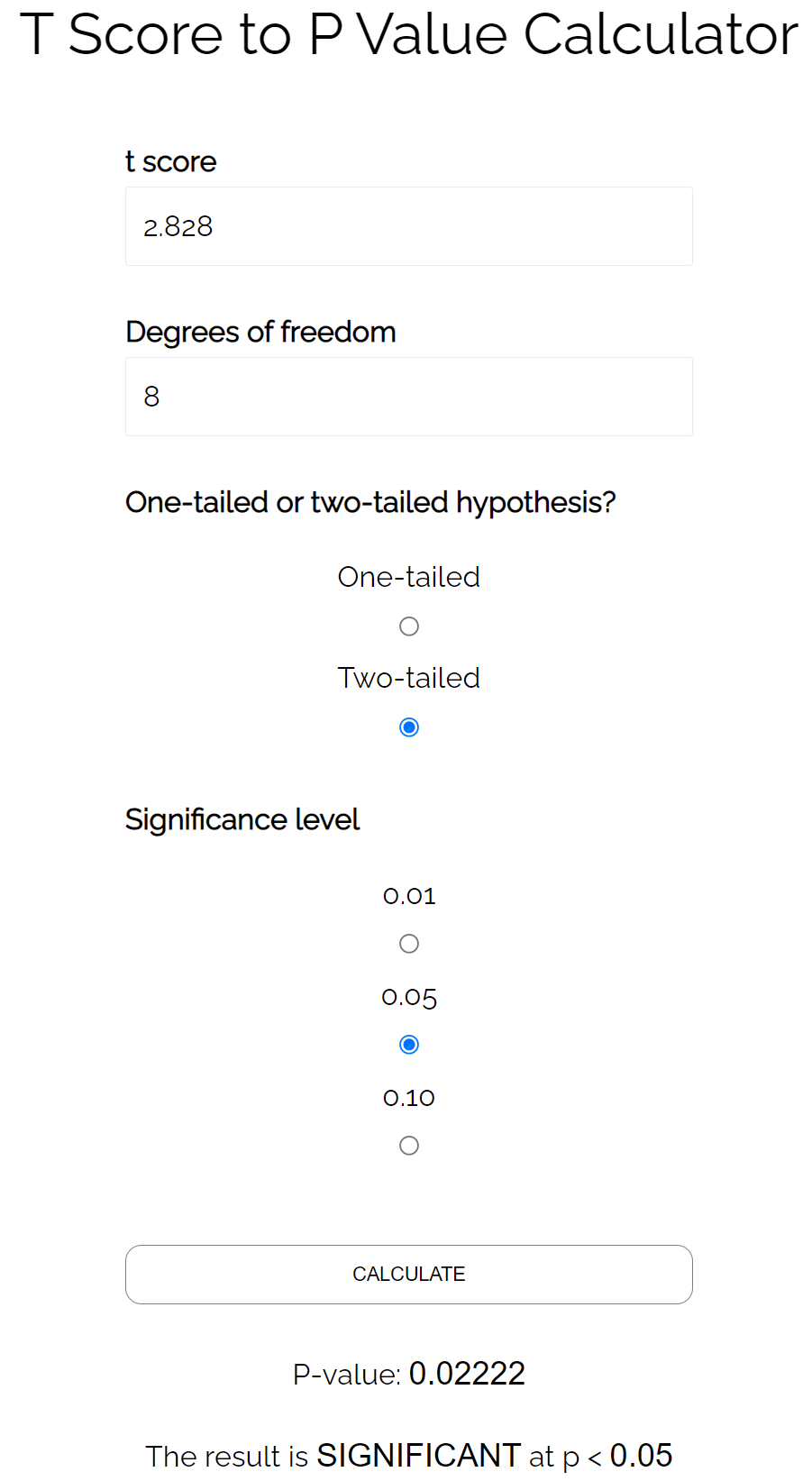
Puisque cette valeur p est inférieure à 0,05, nous conclurions que la corrélation entre ces deux variables est statistiquement significative.

Ressources additionnelles

Comment effectuer un test de corrélation dans Excel
Comment effectuer un test de corrélation dans R
Qu’est-ce qui est considéré comme une corrélation « faible » ?
Qu’est-ce qui est considéré comme une corrélation « forte » ?