Comment effectuer des tests t dans Google Sheets
D’une manière générale, il existe trois types de tests t :
- Un échantillon de test t
- Test T à deux échantillons
- Test t pour échantillons appariés
Ce didacticiel fournit des exemples sur la manière d’effectuer chacun de ces tests dans Google Sheets.
Exemple : un test t sur un échantillon
Définition : Un test t sur un échantillon est utilisé pour tester si la moyenne d’une population est égale ou non à une certaine valeur.
Exemple : Un botaniste veut savoir si la hauteur moyenne d’une certaine espèce de plante est égale à 15 pouces. Elle prélève un échantillon aléatoire de 12 plantes et enregistre chacune de leurs hauteurs en pouces.
La capture d’écran suivante montre comment effectuer un test t sur un échantillon pour déterminer si la taille moyenne réelle de la population est égale à 15 pouces :
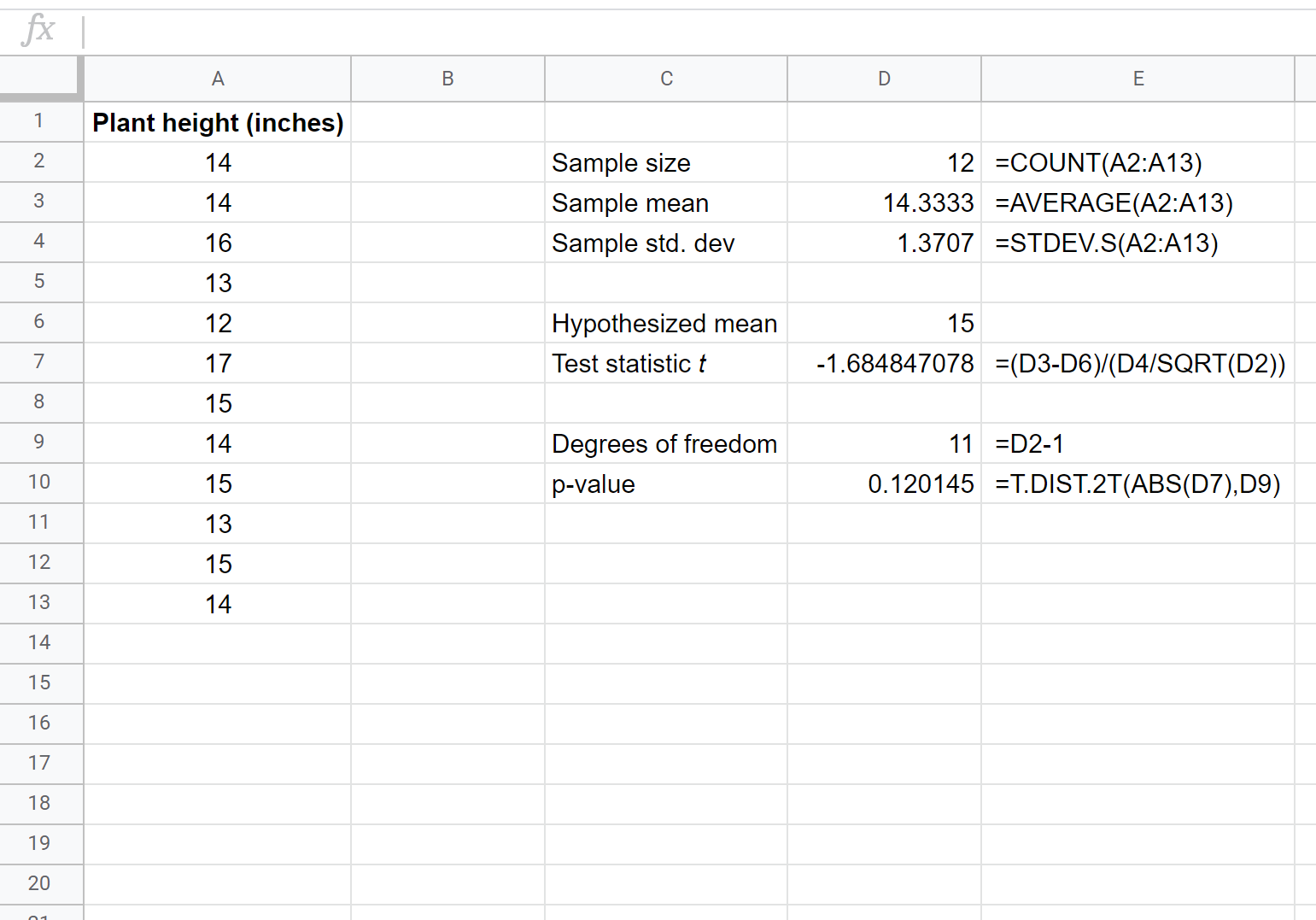
Les deux hypothèses pour ce test t sur un échantillon particulier sont les suivantes :
H 0 : µ = 15 (la hauteur moyenne de cette espèce de plante est de 15 pouces)
H A : µ ≠15 (la hauteur moyenne n’est pas de 15 pouces)
La valeur p de notre test (0,120145) étant supérieure à alpha = 0,05, nous ne parvenons pas à rejeter l’hypothèse nulle du test. Nous ne disposons pas de preuves suffisantes pour affirmer que la hauteur moyenne de cette espèce particulière de plante est différente de 15 pouces.
Exemple : test t à deux échantillons
Définition : Un test t à deux échantillons est utilisé pour tester si les moyennes de deux populations sont égales ou non.
Exemple : Les chercheurs veulent savoir si deux espèces de plantes différentes dans un pays donné ont la même hauteur moyenne. Ils collectent un échantillon aléatoire de 20 plantes de chaque espèce et enregistrent la hauteur de chaque plante en pouces.
La capture d’écran suivante montre comment effectuer un test t à deux échantillons à l’aide de la fonction T.TEST() pour déterminer si les hauteurs moyennes des deux populations sont égales :
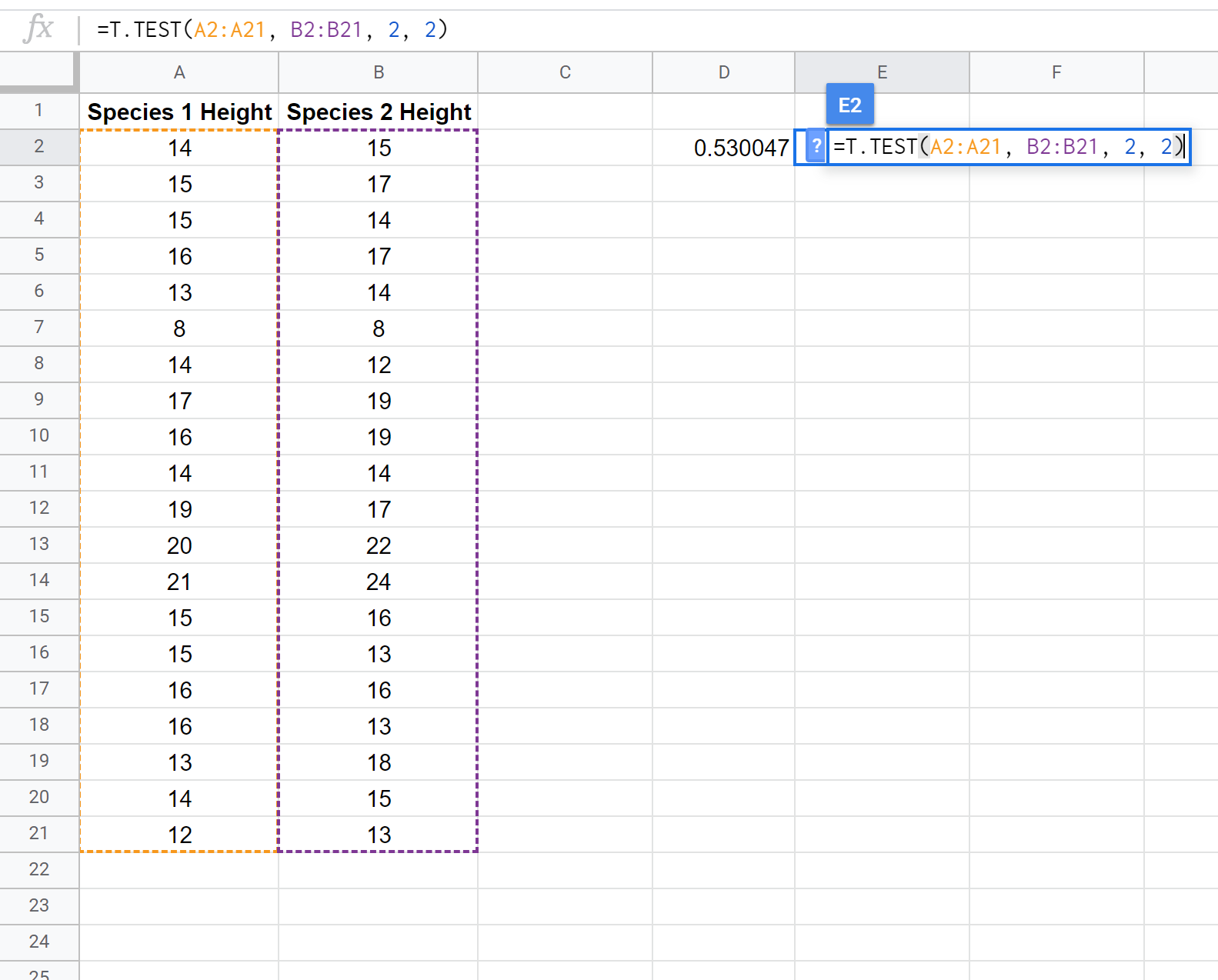
Remarque : Il est également possible d’effectuer un test t unilatéral à deux échantillons avec ou sans l’hypothèse que les deux échantillons ont la même variance. Reportez-vous à la documentation T.TEST pour voir comment ajuster les hypothèses du test.
Les deux hypothèses pour ce test t à deux échantillons sont les suivantes :
H 0 : μ 1 = μ 2 (les deux moyennes de population sont égales)
H 1 : μ 1 ≠ μ 2 (les deux moyennes de population ne sont pas égales)
Parce que la valeur p de notre test (0,530047) est supérieure à alpha = 0,05, nous ne parvenons pas à rejeter l’hypothèse nulle du test. Nous ne disposons pas de preuves suffisantes pour affirmer que la hauteur moyenne de cette espèce particulière de plante est différente de 15 pouces.
Exemple : test t pour échantillons appariés
Définition : Un test t pour échantillons appariés est utilisé pour comparer les moyennes de deux échantillons lorsque chaque observation d’un échantillon peut être associée à une observation de l’autre échantillon.
Exemple : Nous voulons savoir si un programme d’études a un impact significatif sur les performances des étudiants à un examen particulier. Pour tester cela, nous demandons à 20 élèves d’une classe de passer un pré-test. Ensuite, nous faisons participer chacun des étudiants au programme d’études pendant deux semaines. Ensuite, les étudiants repassent un test de difficulté similaire.
La capture d’écran suivante montre comment effectuer un test t sur échantillon apparié pour comparer la différence entre les scores moyens du premier et du deuxième test :
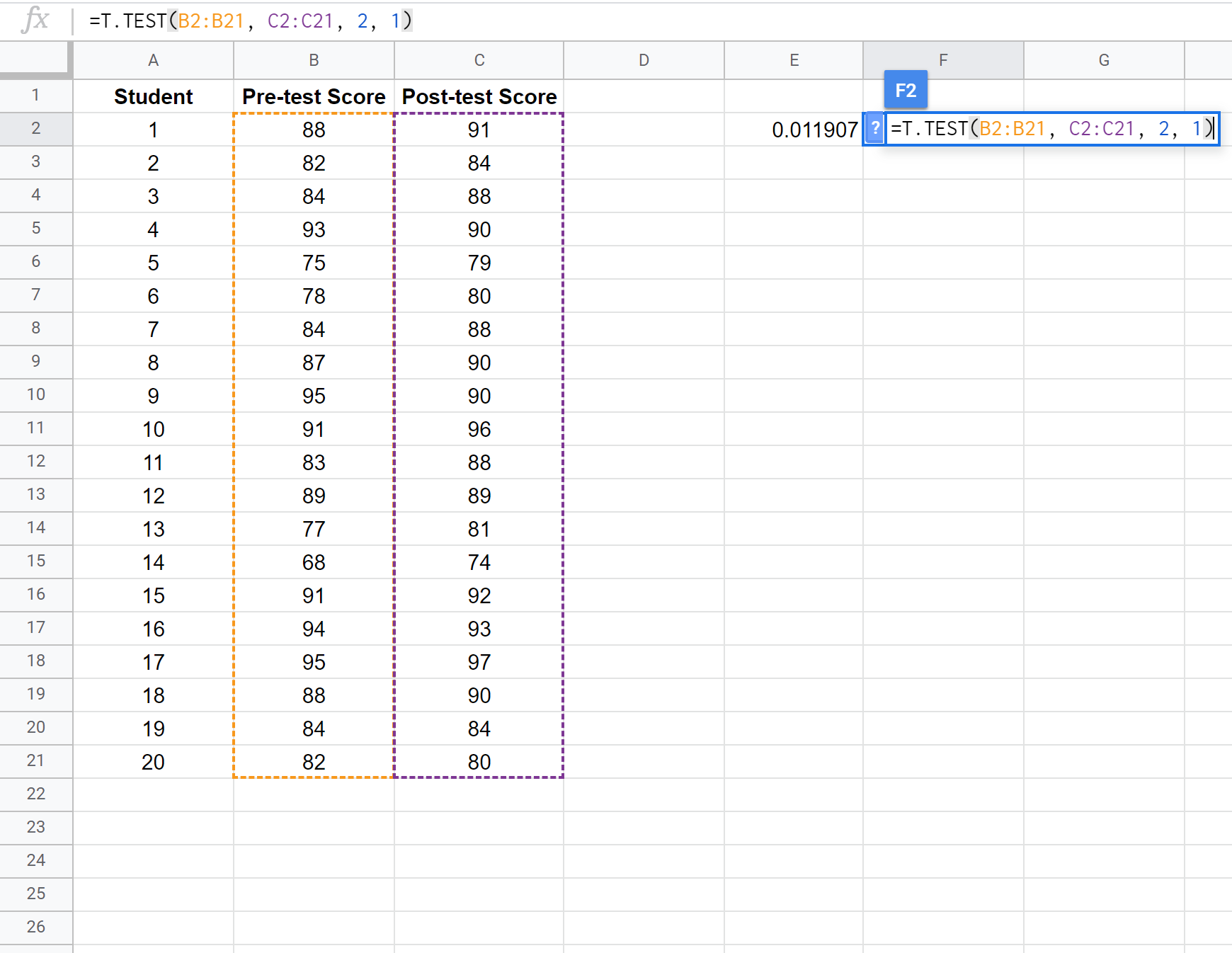
Remarque : Il est également possible d’effectuer un test t unilatéral à deux échantillons avec ou sans l’hypothèse que les deux échantillons ont la même variance. Reportez-vous à la documentation T.TEST pour voir comment ajuster les hypothèses du test.
Les deux hypothèses pour ce test t pour échantillons appariés sont les suivantes :
H 0 : μ 1 = μ 2 (les deux moyennes de population sont égales)
H 1 : μ 1 ≠ μ 2 (les deux moyennes de population ne sont pas égales)
La valeur p de notre test (0,011907) étant inférieure à alpha = 0,05, nous rejetons l’hypothèse nulle du test. Nous disposons de suffisamment de preuves pour affirmer qu’il existe une différence statistiquement significative entre le score moyen pré-test et post-test.
à propos de l'auteur
Dr. Benjamin Anderson
Il est un professeur de statistiques à la retraite devenu éducateur dévoué sur Statorials. Avec une vaste expérience et une expertise dans le domaine des statistiques, je m'engage à partager mes connaissances pour responsabiliser les étudiants grâce à Statorials. Lire plus