Taille de l’échantillon

Par Pr Amélia Rodriguez août 3, 2023 Statistiques 0 commentaire

Cet article explique ce qu’est la taille de l’échantillon et pourquoi elle est importante dans les statistiques. De plus, vous découvrirez comment calculer la taille d’échantillon appropriée et un exercice résolu afin que vous puissiez voir comment cela est fait.

Quelle est la taille de l’échantillon ?

La taille de l’échantillon (ou taille de l’échantillon ) est le nombre d’individus qui composent l’échantillon d’une étude. En statistique, la taille de l’échantillon est importante afin que l’échantillon soit représentatif de l’ensemble de la population.

Par conséquent, la taille de l’échantillon d’une étude statistique doit être suffisamment grande pour représenter les caractéristiques de l’ensemble de la population. En revanche, la taille de l’échantillon ne peut pas être excessivement grande, car la recherche devient alors plus coûteuse. En conclusion, la taille de l’échantillon doit être adéquate, ni trop grande ni trop petite.

Par exemple, si l’on veut faire une analyse sur la hauteur d’un pays, on ne peut pas demander la taille de tous les habitants du pays, car l’enquête prendrait beaucoup de temps et serait trop coûteuse. Il faut donc procéder à un échantillonnage aléatoire et interroger uniquement un échantillon représentatif de la population.

➤ Voir : Types d’échantillonnage

Et comment pouvons-nous connaître la taille d’échantillon appropriée ? Dans la section suivante, nous verrons comment déterminer la taille d’échantillon appropriée en fonction des exigences de la recherche.

Comment calculer la taille de l’échantillon

Pour l’estimation d’une moyenne, la taille d’échantillon nécessaire est égale au carré de Z _α/2 multiplié par l’écart type (σ) divisé par la marge d’erreur souhaitée (e). La formule pour calculer la taille de l’échantillon est donc la suivante :

$\displaystyle n=\left(\frac{Z_{\alpha/2}\cdot\sigma}{e}\right)^2$

Où:

$n$ est la taille de l’échantillon.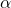
$\alpha$ est le niveau de signification souhaité. En tenant compte de ce 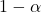$1-\alpha$ est le niveau de confiance souhaité.
$Z_{\alpha/2}$ est le quantile de la distribution normale standard correspondant à une probabilité de α/2. Pour des échantillons de grande taille et un niveau de confiance de 95 %, il est généralement proche de 1,96 et pour un niveau de confiance de 99 %, il est généralement proche de 2,576.
$\sigma$ est l’écart type.

Gardez à l’esprit que dans cette formule, on suppose que la taille de la population est infinie, c’est-à-dire que la taille de la population est très grande ou inconnue.

Remarque : La formule ci-dessus est dérivée de la formule de l’intervalle de confiance pour la moyenne .

Exemple de calcul de la taille de l’échantillon

Dans cette section, nous calculerons la taille d’échantillon appropriée pour une enquête statistique à titre d’exemple.

On sait que l’écart type d’une population est d’environ 15, mais on ne connaît pas sa moyenne, on souhaite donc réaliser une étude pour estimer la moyenne. Quelle est la taille de l’échantillon dont nous avons besoin si nous voulons une marge d’erreur de ±2 avec un niveau de confiance de 95 % ?

Comme nous l’avons vu ci-dessus, la formule pour calculer la taille de l’échantillon est la suivante :

$\displaystyle n=\left(\frac{Z_{\alpha/2}\cdot\sigma}{e}\right)^2$

Dans ce cas, le niveau de confiance souhaité est de 95 %, donc la valeur Z _α/2 correspondante est de 1,96.

$1-\alpha=0,95 \ \color{orange}\bm{\longrightarrow}\color{black} \ \alpha=0,05 \ \color{orange}\bm{\longrightarrow}\color{black}\ \alpha/2=0,025$

$\begin{array}{c}Z_{\alpha/2}= \ \color{orange}\bm{?}\\[4ex]Z_{0,025}=1,96\end{array}$

➤ Voir : Tableau avec les valeurs des niveaux de confiance

Enfin, maintenant que nous savons combien valent tous les paramètres, nous substituons leurs valeurs dans la formule et calculons la taille de l’échantillon :

$\begin{aligned}\displaystyle n&=\left(\frac{Z_{\alpha/2}\cdot\sigma}{e}\right)^2\\[2ex] n&=\left(\frac{1,96\cdot 15}{2}\right)^2\\[2ex] n&=216,09 \approx 217 \end{array}$

En bref, pour estimer la moyenne de la population avec les exigences souhaitées, nous avons besoin d’au moins un échantillon de 217 individus.

Taille de l’échantillon, niveau de confiance et marge d’erreur

En fonction du niveau de confiance et de la marge d’erreur exigée, la taille de l’échantillon nécessaire variera. Ainsi, la taille de l’échantillon, le niveau de confiance et la marge d’erreur sont liés comme suit :

La taille de l’échantillon et le niveau de confiance sont directement proportionnels. Autrement dit, si le niveau de confiance augmente, la taille de l’échantillon augmentera également.
La taille de l’échantillon et la marge d’erreur sont inversement proportionnelles. Ainsi, si la marge d’erreur augmente, la taille de l’échantillon diminuera.
Par conséquent, augmenter la taille de l’échantillon peut augmenter le niveau de confiance ou réduire la marge d’erreur.

Autres formules de taille d’échantillon

En fonction du paramètre à estimer, la formule pour la taille d’échantillon nécessaire varie légèrement. Par conséquent, dans cette section, nous verrons d’autres formules qui peuvent être utiles pour calculer la taille de l’échantillon dans certains cas particuliers.

taille de l’échantillon d’une proportion

La formule pour calculer la taille d’échantillon nécessaire pour estimer une proportion (p) est la suivante :

$n=\cfrac{N\cdot Z_{\alpha/2}^2\cdot p\cdot (1-p)}{e^2\cdot (N-1)+Z_{\alpha/2}^2\cdot p\cdot (1-p)}$

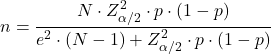
Taille de l’échantillon d’une probabilité

Lorsque vous souhaitez estimer une probabilité, il est recommandé d’utiliser la formule suivante pour déterminer la taille d’échantillon nécessaire :

$\displaystyle n=\left(\frac{Z_{\alpha/2}}{2\cdot e}\right)^2$

Taille de l’échantillon pour la comparaison de deux moyennes indépendantes

La formule pour calculer la taille de l’échantillon lors de la comparaison de deux moyennes indépendantes avec un risque α et un risque β donnés est la suivante :

$n=\cfrac{2\cdot \sigma^2 \cdot \left(Z_{\alpha/2}+Z_\beta\right)}{\Delta^2}$

Où

$\Delta$ est la différence entre les deux moyennes de l’hypothèse alternative.

Taille de l’échantillon pour la comparaison de deux moyennes appariées

Si vous souhaitez comparer deux moyennes appariées avec une erreur α et une erreur β fixes, la formule à utiliser pour trouver le nombre d’observations dans l’échantillon est la suivante :

$n=\cfrac{2\cdot \sigma_d^2 \cdot \left(Z_{\alpha/2}+Z_\beta\right)}{\Delta^2}$

Où

$\Delta$ est la différence entre les deux moyennes appariées de l’hypothèse alternative et $\sigma_d^2$ C’est la variance des différences entre deux mesures d’un même individu.

à propos de l'auteur

Pr Amélia Rodriguez

En mettant l'accent sur l'apprentissage interactif et les applications pratiques, la professeure Amélia Rodriguez propose des tutoriels complets et des exemples concrets pour rendre les concepts de probabilité accessibles et pertinents pour la vie de ses étudiants. Lire plus