Taille de l’effet : qu’est-ce que c’est et pourquoi c’est important
« La signification statistique est la chose la moins intéressante des résultats. Vous devez décrire les résultats en termes de mesures d’ampleur – non seulement, un traitement affecte-t-il les gens, mais dans quelle mesure il les affecte. -Gene V. Verre
En statistiques, nous utilisons souvent les valeurs p pour déterminer s’il existe une différence statistiquement significative entre deux groupes.
Par exemple, supposons que nous voulions savoir si deux techniques d’étude différentes conduisent à des résultats différents aux tests. Ainsi, nous avons un groupe de 20 étudiants qui utilisent une technique d’étude pour se préparer à un test tandis qu’un autre groupe de 20 étudiants utilise une technique d’étude différente. Nous faisons ensuite passer à chaque élève le même test.
Après avoir exécuté un test t sur deux échantillons pour déterminer une différence de moyenne, nous constatons que la valeur p du test est de 0,001. Si nous utilisons un niveau de signification de 0,05, cela signifie qu’il existe une différence statistiquement significative entre les résultats moyens des deux groupes. Ainsi, la technique d’étude a un impact sur les résultats des tests.
Cependant, même si la valeur p nous indique que la technique d’étude a un impact sur les résultats aux tests, elle ne nous indique pas l’ ampleur de cet impact. Pour comprendre cela, nous devons connaître la taille de l’effet .
Qu’est-ce que la taille de l’effet ?
Une taille d’effet est un moyen de quantifier la différence entre deux groupes.
Alors qu’une valeur p peut nous indiquer s’il existe ou non une différence statistiquement significative entre deux groupes, une taille d’effet peut nous indiquer l’ampleur réelle de cette différence. En pratique, les tailles d’effet sont bien plus intéressantes et utiles à connaître que les valeurs p.
Il existe trois façons de mesurer l’ampleur de l’effet, selon le type d’analyse que vous effectuez :
1. Différence moyenne standardisée
Lorsque vous souhaitez étudier la différence moyenne entre deux groupes, la manière appropriée de calculer la taille de l’effet consiste à utiliser une différence moyenne standardisée . La formule la plus populaire à utiliser est connue sous le nom de d de Cohen, qui est calculée comme suit :
D de Cohen = ( x 1 – x 2 ) / s
où x 1 et x 2 sont respectivement les moyennes d’échantillon du groupe 1 et du groupe 2, et s est l’écart type de la population à partir de laquelle les deux groupes ont été tirés.
En utilisant cette formule, la taille de l’effet est facile à interpréter :
- Un d de 1 indique que les moyennes des deux groupes diffèrent d’un écart type.
- Un d de 2 signifie que les moyennes du groupe diffèrent de deux écarts types.
- Un d de 2,5 indique que les deux moyennes diffèrent de 2,5 écarts types, et ainsi de suite.
Une autre façon d’interpréter la taille de l’effet est la suivante : une taille d’effet de 0,3 signifie que le score de la personne moyenne du groupe 2 est de 0,3 écart-type au-dessus de la personne moyenne du groupe 1 et dépasse donc les scores de 62 % de celles du groupe 1 . .
Le tableau suivant présente différentes tailles d’effet et leurs percentiles correspondants :
| Taille de l’effet | Pourcentage du groupe 2 qui serait en dessous de la moyenne des personnes du groupe 1 |
|---|---|
| 0,0 | 50% |
| 0,2 | 58% |
| 0,4 | 66% |
| 0,6 | 73% |
| 0,8 | 79% |
| 1.0 | 84% |
| 1.2 | 88% |
| 1.4 | 92% |
| 1.6 | 95% |
| 1.8 | 96% |
| 2.0 | 98% |
| 2.5 | 99% |
| 3.0 | 99,9% |
Plus la taille de l’effet est grande, plus la différence entre l’individu moyen de chaque groupe est grande.
En général, un d de 0,2 ou moins est considéré comme une taille d’effet de petite taille, un d d’environ 0,5 est considéré comme une taille d’effet moyenne et un d de 0,8 ou plus est considéré comme une taille d’effet importante.
Ainsi, si les moyennes de deux groupes ne diffèrent pas d’au moins 0,2 écart-type, la différence est insignifiante, même si la valeur p est statistiquement significative.
2. Coefficient de corrélation
Lorsque vous souhaitez étudier la relation quantitative entre deux variables, le moyen le plus courant de calculer la taille de l’effet consiste à utiliser le coefficient de corrélation de Pearson . Il s’agit d’une mesure de l’association linéaire entre deux variables X et Y. Elle a une valeur comprise entre -1 et 1 où :
- -1 indique une corrélation linéaire parfaitement négative entre deux variables
- 0 indique aucune corrélation linéaire entre deux variables
- 1 indique une corrélation linéaire parfaitement positive entre deux variables
La formule pour calculer le coefficient de corrélation de Pearson est assez complexe, mais elle peut être trouvée ici pour ceux qui sont intéressés.
Plus le coefficient de corrélation s’éloigne de zéro, plus la relation linéaire entre deux variables est forte. Cela peut également être constaté en créant un simple nuage de points des valeurs des variables X et Y .
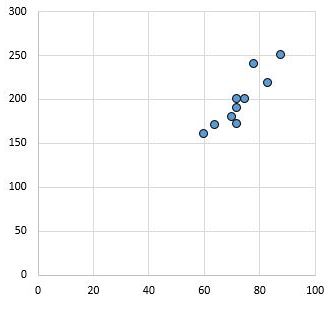
Par exemple, le nuage de points suivant montre les valeurs de deux variables ayant un coefficient de corrélation de r = 0,94.
Cette valeur est loin d’être nulle, ce qui indique qu’il existe une forte relation positive entre les deux variables.
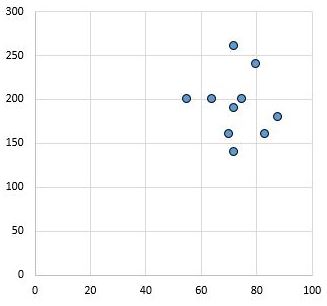
À l’inverse, le nuage de points suivant montre les valeurs de deux variables qui ont un coefficient de corrélation de r = 0,03. Cette valeur est proche de zéro, ce qui indique qu’il n’y a pratiquement aucune relation entre les deux variables.
En général, l’ampleur de l’effet est considérée comme faible si la valeur du coefficient de corrélation de Pearson r est d’environ 0,1, moyenne si r est d’environ 0,3 et grande si r est égal ou supérieur à 0,5.
3. Rapport de cotes
Lorsque vous souhaitez étudier les chances de succès dans un groupe de traitement par rapport aux chances de succès dans un groupe témoin, la méthode la plus courante pour calculer l’ampleur de l’effet consiste à utiliser le rapport de cotes .
Par exemple, supposons que nous ayons le tableau suivant :
| Taille de l’effet | # Succès | # Les échecs |
|---|---|---|
| Groupe de traitement | UN | B |
| Groupe de contrôle | C | D |
Le rapport de cotes serait calculé comme suit :
Rapport de cotes = (AD) / (BC)
Plus l’odds ratio s’éloigne de 1, plus la probabilité que le traitement produise un effet réel est élevée.
Les avantages de l’utilisation des tailles d’effet par rapport aux valeurs P
Les tailles d’effet présentent plusieurs avantages par rapport aux valeurs p :
1. Une taille d’effet nous aide à avoir une meilleure idée de l’ampleur de la différence entre deux groupes ou de la force de l’association entre deux groupes. Une valeur p peut seulement nous dire s’il existe ou non une différence significative ou une association significative.
2. Contrairement aux valeurs p, les tailles d’effet peuvent être utilisées pour comparer quantitativement les résultats de différentes études réalisées dans différents contextes. Pour cette raison, les tailles d’effet sont souvent utilisées dans les méta-analyses.
3. Les valeurs P peuvent être affectées par des échantillons de grande taille. Plus la taille de l’échantillon est grande, plus la puissance statistique d’un test d’hypothèse est grande, ce qui lui permet de détecter même des effets minimes. Cela peut conduire à des valeurs p faibles, malgré de petites tailles d’effet qui peuvent n’avoir aucune signification pratique.
Un exemple simple peut illustrer cela clairement : supposons que nous souhaitions savoir si deux techniques d’étude conduisent à des résultats différents aux tests. Nous avons un groupe de 20 étudiants qui utilisent une technique d’étude tandis qu’un autre groupe de 20 étudiants utilise une technique d’étude différente. Nous faisons ensuite passer à chaque élève le même test.
Le score moyen du groupe 1 est de 90,65 et le score moyen du groupe 2 est de 90,75 . L’écart type pour l’échantillon 1 est de 2,77 et l’écart type pour l’échantillon 2 est de 2,78 .
Lorsque nous effectuons un test t indépendant sur deux échantillons, il s’avère que la statistique du test est de -0,113 et la valeur p correspondante est de 0,91 . La différence entre les résultats moyens des tests n’est pas statistiquement significative.
Cependant, considérons si les tailles d’échantillon des deux échantillons étaient toutes deux de 200 , mais que les moyennes et les écarts types restaient exactement les mêmes.
Dans ce cas, un test t indépendant sur deux échantillons révélerait que la statistique du test est de -1,97 et que la valeur p correspondante est juste en dessous de 0,05 . La différence entre les résultats moyens des tests est statistiquement significative.
La raison sous-jacente pour laquelle des échantillons de grande taille peuvent conduire à des conclusions statistiquement significatives est due à la formule utilisée pour calculer les statistiques de test t :
statistique de test t = [ ( x 1 – x 2 ) – d ] / (√ s 2 1 / n 1 + s 2 2 / n 2 )
Notez que lorsque n 1 et n 2 sont petits, le dénominateur entier de la statistique de test t est petit. Et quand on divise par un petit nombre, on obtient un grand nombre. Cela signifie que la statistique de test t sera grande et la valeur p correspondante sera petite, conduisant ainsi à des résultats statistiquement significatifs.
Qu’est-ce qui est considéré comme une bonne taille d’effet ?
Une question que les étudiants se posent souvent est la suivante : qu’est-ce qui est considéré comme une bonne taille d’effet ?
La réponse courte : une taille d’effet ne peut pas être « bonne » ou « mauvaise » puisqu’elle mesure simplement la taille de la différence entre deux groupes ou la force de l’association entre deux groupes.
Cependant, nous pouvons utiliser les règles empiriques suivantes pour quantifier si l’ampleur d’un effet est petite, moyenne ou grande :
Le D de Cohen :
- Un d de 0,2 ou moins est considéré comme une petite taille d’effet.
- Un d de 0,5 est considéré comme une taille d’effet moyenne.
- Un d de 0,8 ou plus est considéré comme une taille d’effet importante.
Coefficient de corrélation de Pearson
- Une valeur absolue de r autour de 0,1 est considérée comme une taille d’effet faible.
- Une valeur absolue de r autour de 0,3 est considérée comme une ampleur d’effet moyenne.
- Une valeur absolue de r supérieure à 0,5 est considérée comme une taille d’effet importante.
Cependant, la définition d’une corrélation « forte » peut varier d’un domaine à l’autre. Reportez-vous àcet article pour mieux comprendre ce qui est considéré comme une forte corrélation dans différents secteurs.
