4 exemples d’utilisation des tests du chi carré dans la vie réelle
En statistiques, il existe deux types différents de tests du Chi carré :
1. Le test d’ajustement du chi carré – Utilisé pour déterminer si une variable catégorielle suit ou non une distribution hypothétique.
2. Le test d’indépendance du chi carré – Utilisé pour déterminer s’il existe ou non une association significative entre deux variables catégorielles.
Dans cet article, nous partageons plusieurs exemples de la façon dont chacun de ces types de tests du Chi carré est utilisé dans des situations réelles.
Exemple 1 : Test d’adéquation du chi carré
Supposons qu’un propriétaire de magasin affirme qu’un nombre égal de clients viennent dans son magasin chaque jour de la semaine.
Pour tester cette hypothèse, il enregistre le nombre de clients qui viennent dans le magasin une semaine donnée et constate ce qui suit :
- Lundi : 50 clients
- Mardi : 60 clients
- Mercredi : 40 clients
- Jeudi : 47 clients
- Vendredi : 53 clients
Il peut utiliser un test d’adéquation du chi carré pour déterminer si la répartition des clients qui viennent chaque jour est cohérente avec son hypothèse de distribution.
À l’aide du calculateur de test d’adéquation du chi carré , il peut constater que la valeur p du test est de 0,359 .
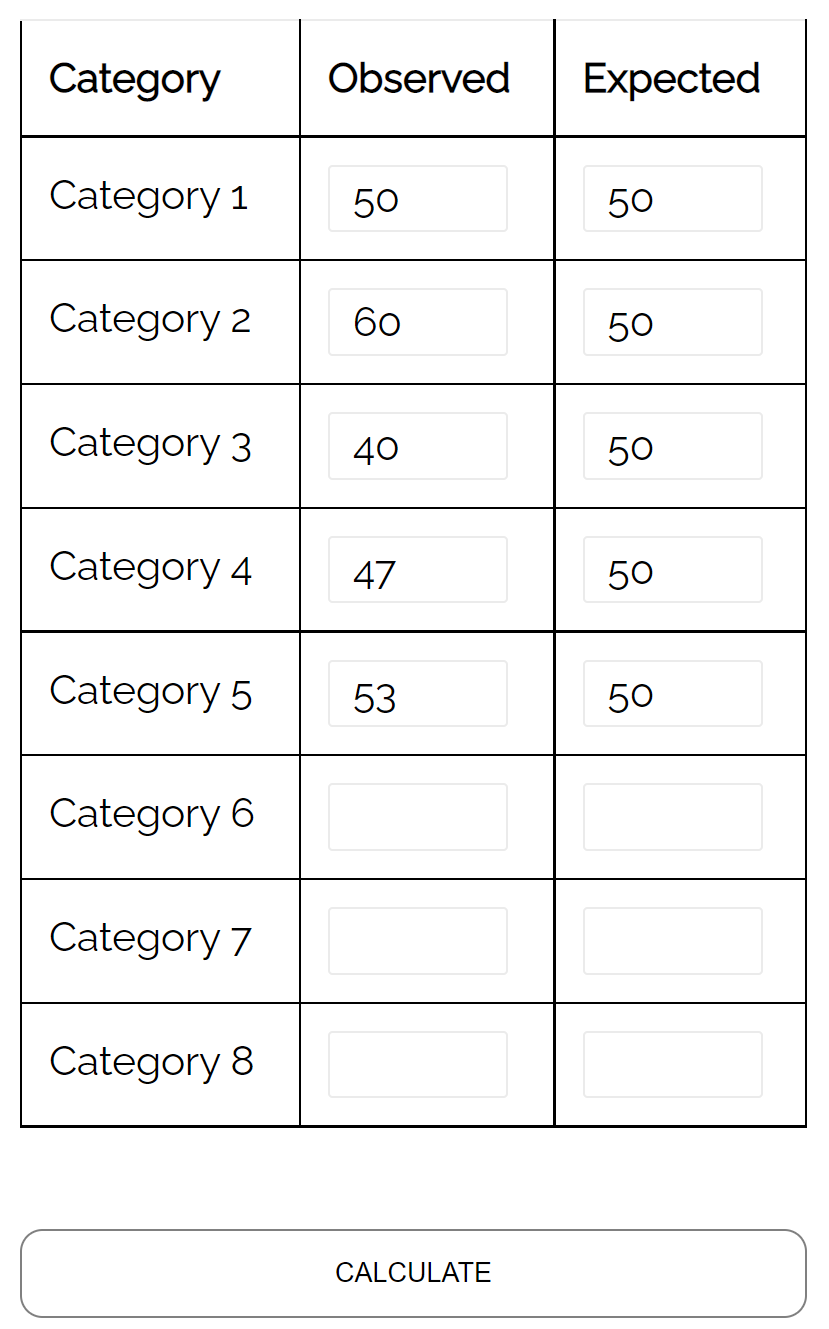
Étant donné que cette valeur p n’est pas inférieure à 0,05, il n’y a pas de preuves suffisantes pour affirmer que la véritable répartition des clients est différente de celle revendiquée par le propriétaire du magasin.
Exemple 2 : Test d’adéquation du chi carré
Supposons qu’un biologiste affirme qu’un nombre égal de quatre espèces différentes de cerfs pénètrent chaque semaine dans une certaine zone boisée d’une forêt.
Pour tester cette hypothèse, elle enregistre le nombre de chaque espèce de cerf qui pénètre dans la zone boisée au cours d’une semaine :
- Espèce n°1 : 22
- Espèce #2 : 20
- Espèce #3 : 23
- Espèce #4 : 35
Elle peut utiliser un test d’adéquation du chi carré pour déterminer si la répartition des espèces de cerfs qui pénètrent dans la zone boisée de la forêt chaque semaine est cohérente avec sa répartition hypothétique.
À l’aide du calculateur de test d’adéquation du chi carré , elle peut constater que la valeur p du test est de 0,137 .
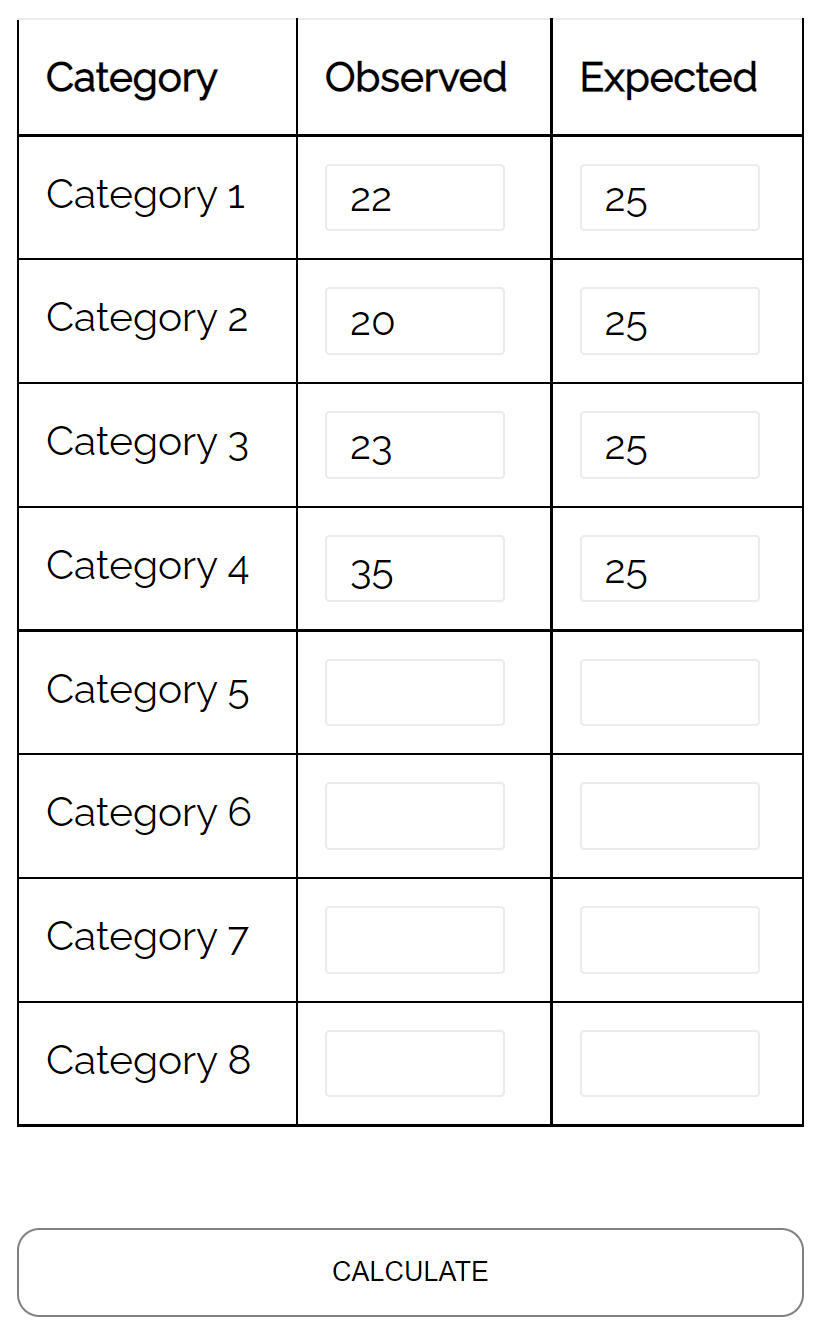
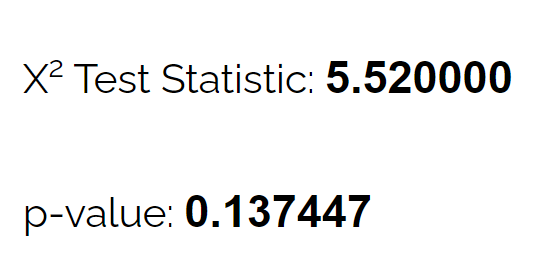
Étant donné que cette valeur p n’est pas inférieure à 0,05, il n’y a pas de preuves suffisantes pour affirmer que la véritable répartition des cerfs est différente de celle revendiquée par le biologiste.
Exemple 3 : Test d’indépendance du chi carré
Supposons qu’un décideur politique d’une certaine ville veuille savoir si le genre est associé ou non à la préférence d’un parti politique.
Il décide de prélever un échantillon aléatoire simple de 500 électeurs et de les interroger sur leur préférence en matière de parti politique. Le tableau suivant présente les résultats de l’enquête :
| Républicain | Démocrate | Indépendant | Total | |
| Mâle | 120 | 90 | 40 | 250 |
| Femelle | 110 | 95 | 45 | 250 |
| Total | 230 | 185 | 85 | 500 |
Il peut utiliser un test d’indépendance du chi carré pour déterminer s’il existe une association statistiquement significative entre les deux variables.
À l’aide du calculateur du test d’indépendance du chi carré , il peut constater que la valeur p du test est de 0,649 .
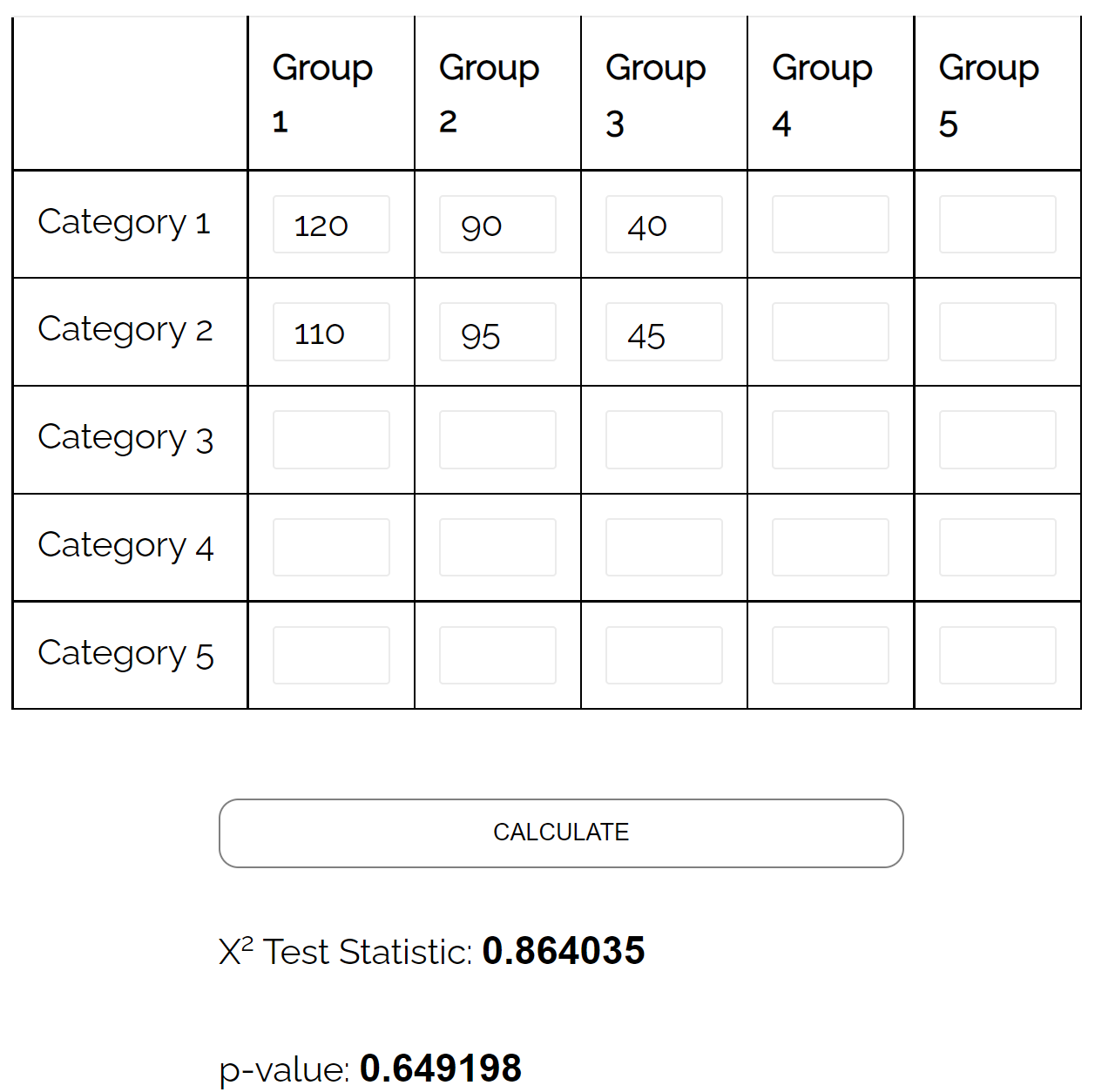
Étant donné que la valeur p n’est pas inférieure à 0,05, il n’existe pas de preuves suffisantes pour affirmer qu’il existe une association entre le sexe et la préférence pour un parti politique.
Exemple 4 : Test d’indépendance du chi carré
Supposons qu’un chercheur veuille savoir si l’état matrimonial est associé ou non au niveau d’éducation.
Il décide de prélever un échantillon aléatoire simple de 300 individus et obtient les résultats suivants :
| Lycée | Les bacheliers | Master ou supérieur | Total | |
| Marié | 20 | 100 | 35 | 155 |
| Célibataire | 50 | 80 | 15 | 145 |
| Total | 70 | 180 | 50 | 300 |
Il peut utiliser un test d’indépendance du chi carré pour déterminer s’il existe une association statistiquement significative entre les deux variables.
À l’aide du calculateur du test d’indépendance du chi carré , il peut constater que la valeur p du test est de 0,000011 .
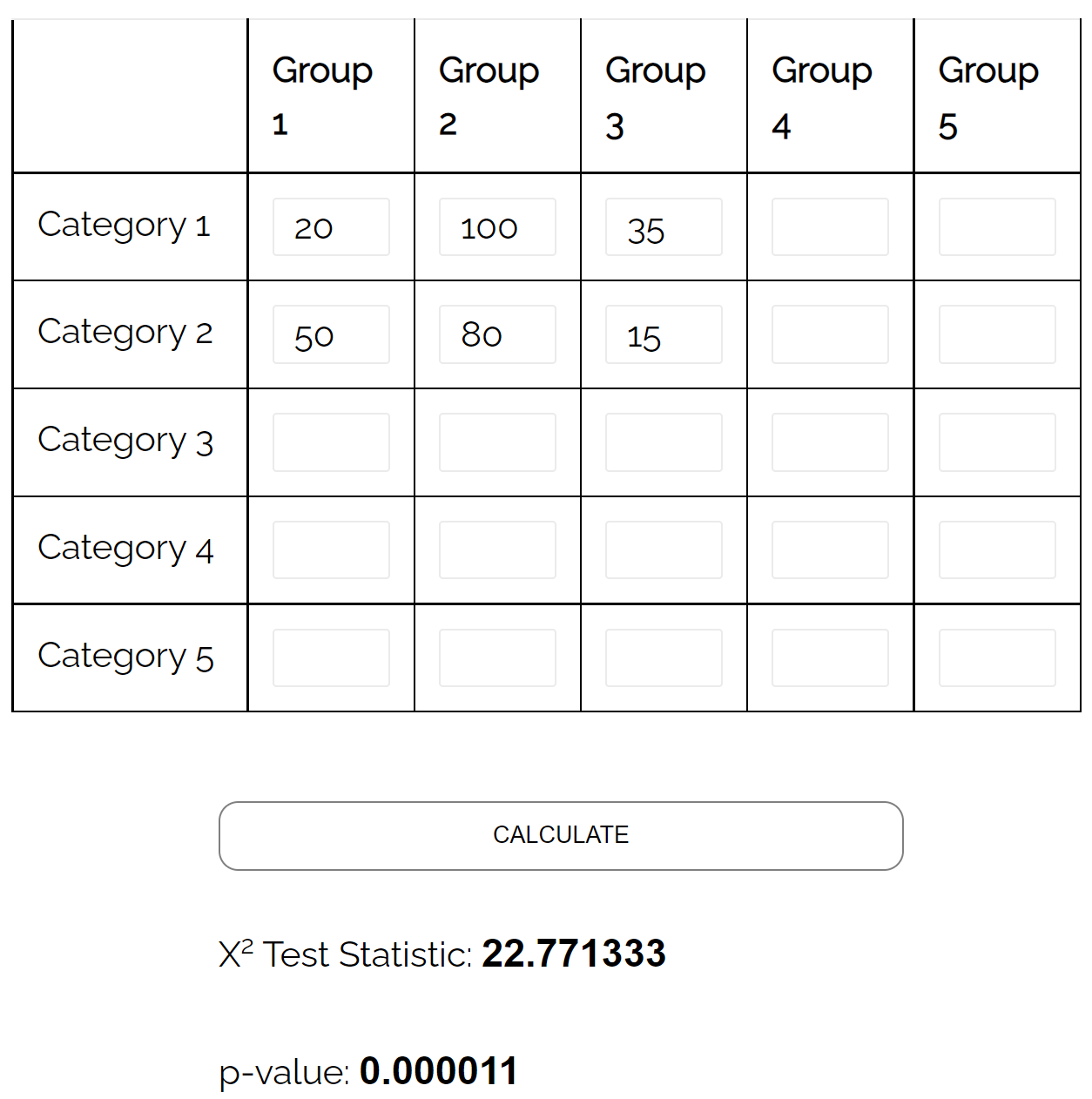
Puisque la valeur p est inférieure à 0,05, il existe suffisamment de preuves pour affirmer qu’il existe une association entre l’état matrimonial et le niveau d’éducation.
Ressources additionnelles
Les didacticiels suivants fournissent une introduction aux différents types de tests du Chi carré :
Les didacticiels suivants expliquent la différence entre les tests du Chi carré et d’autres tests statistiques :
à propos de l'auteur
Dr. Benjamin Anderson
Il est un professeur de statistiques à la retraite devenu éducateur dévoué sur Statorials. Avec une vaste expérience et une expertise dans le domaine des statistiques, je m'engage à partager mes connaissances pour responsabiliser les étudiants grâce à Statorials. Lire plus