Test d’hypothèse pour la variance

Par Pr Amélia Rodriguez août 3, 2023 Statistiques 0 commentaire

Cet article explique ce qu’est le test d’hypothèse pour la variance. Ainsi, vous trouverez la formule du test d’hypothèse sur la variance et, en plus, un exercice résolu étape par étape.

Qu’est-ce que le test d’hypothèse pour la variance ?

Le test d’hypothèse pour la variance est une méthode statistique utilisée pour déterminer s’il faut ou non rejeter l’hypothèse nulle d’une variance de population. Autrement dit, le test d’hypothèse sur la variance sert à rejeter ou à accepter l’hypothèse sur la valeur de la variance d’une population.

Plus précisément, en fonction de la valeur de la statistique du test d’hypothèse pour la variance et du niveau de signification choisi, l’hypothèse nulle est rejetée ou acceptée.

Gardez à l’esprit que les tests d’hypothèses portent de nombreux noms, ils peuvent également être appelés contrastes d’hypothèses, tests d’hypothèses ou tests de signification.

Formule de test d’hypothèse pour la variance

La statistique du test d’hypothèse pour la variance est égale à la différence entre la taille de l’échantillon moins un multipliée par la variance de l’échantillon et divisée par la valeur proposée de la variance de la population. La statistique du test d’hypothèse pour la variance a une distribution du chi carré .

Ainsi, la formule de calcul de la statistique du test d’hypothèse pour la variance est la suivante :

$\chi^2=\cfrac{(n-1)s^2}{\sigma^2}$

Où:

$\chi^2$ est la statistique de test d’hypothèse pour la variance, qui a une distribution du chi carré.
$n$ est la taille de l’échantillon.
$s^2$ est la variance de l’échantillon.
$\sigma^2$ est la variance de population proposée.

Pour interpréter le résultat de la statistique, la valeur obtenue doit être comparée à la valeur critique du test.

Si le test d’hypothèse pour la variance est bilatéral, l’hypothèse nulle est rejetée si la statistique est supérieure à la valeur critique. $\chi_{1-\alpha/2|n-1}^2$ ou si la valeur critique est inférieure à $\chi_{\alpha/2|n-1}$ .
Si le test d’hypothèse pour la variance correspond à la queue droite, l’hypothèse nulle est rejetée si la statistique est supérieure à la valeur critique $\chi_{1-\alpha|n-1}^2$ .
Si le test d’hypothèse pour la variance correspond à la queue gauche, l’hypothèse nulle est rejetée si la statistique est inférieure à la valeur critique $\chi_{\alpha|n-1}$ .

$\begin{array}{l}H_1: \sigma^2\neq \sigma_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } \chi^2>\chi^2_{1-\alpha/2|n-1}\text{ se rechaza } H_0\\[3ex]H_1: \sigma^2\neq \sigma_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si }\chi^2<\chi^2_{\alpha/2|n-1}\text{ se rechaza } H_0 \\[3ex]H_1: \sigma^2> \sigma_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } \chi^2>\chi^2_{1-\alpha|n-1}\text{ se rechaza } H_0\\[3ex]H_1: \sigma^2< \sigma_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } \chi^2<\chi^2_{\alpha|n-1}\text{ se rechaza } H_0\end{array}$

Les valeurs critiques du test d’hypothèse pour la variance sont obtenues à partir du tableau de distribution du chi carré. Notez que les degrés de liberté pour la distribution du Chi carré correspondent à la taille de l’échantillon moins 1.

Exemple concret de test d’hypothèse pour la variance

Après avoir vu la définition du test d’hypothèse de variance et quelle est sa formule, nous allons voir un exemple concret pour finir d’assimiler le concept.

Une usine possède une machine qui produit des pièces pour une voiture avec une grande précision. On soupçonne cependant qu’elle s’est éloignée et fabrique désormais des pièces avec un écart supérieur à 8 mm ² . Pour réfuter cette hypothèse, un échantillon de 25 pièces est analysé et sa variance d’échantillon est de 9,1 mm ² . L’hypothèse initiale peut-elle être rejetée avec un niveau de signification α=0,05 ?

L’hypothèse nulle et l’hypothèse alternative de ce test d’hypothèse sur la variance sont les suivantes :

$\begin{cases}H_0: \sigma^2=8 \\[2ex] H_1:\sigma^2>8 \end{cases}$

Pour déterminer si l’hypothèse nulle peut être rejetée ou non, nous calculons la statistique du test d’hypothèse pour la variance en utilisant la formule que nous avons vue ci-dessus :

$\chi^2=\cfrac{(n-1)s^2}{\sigma^2}$

$\chi^2=\cfrac{(25-1)\cdot 9,1}{8}$

$\chi^2=27,3$

Nous recherchons maintenant la valeur critique correspondant à la queue droite pour 24 degrés de liberté et un niveau de signification α=0,05 dans le tableau de distribution du Chi carré :

$\begin{array}{c}\chi^2_{1-\alpha|n-1}=\ \color{orange}\bm{?}\color{black}\\[2ex]\chi^2_{0,95|24}=36,415\end{array}$

Ainsi, la statistique calculée est inférieure à la valeur critique du test et donc l’hypothèse nulle du test d’hypothèse de variance n’est pas rejetée, mais plutôt l’hypothèse alternative est rejetée.

$27,3<36,415 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{No se rechaza } H_0$

➤ Voir : Test d’hypothèse pour la moyenne de la population
➤ Voir : Test d’hypothèse pour la proportion de population

Test d’hypothèse pour la variance de deux populations

Les tests d’hypothèses sur la variance de deux populations sont utilisés pour rejeter ou accepter l’hypothèse selon laquelle les variances de deux populations différentes sont égales.

Ainsi l’hypothèse nulle d’un test d’hypothèse sur la variance de deux populations est toujours la suivante :

$H_0: \sigma^2_1=\sigma^2_2$

Et l’hypothèse alternative peut être l’une des trois options suivantes :

$\begin{array}{l}H_1:\sigma^2_1\neq \sigma^2_2\\[2ex]H_1:\sigma^2_1>\sigma^2_2\\[2ex]H_1:\sigma^2_1<\sigma^2_2\end{array}$

Dans ce cas, la formule pour calculer la statistique du test d’hypothèse pour la variance de deux populations est la suivante :

$F=\cfrac{s_1^2}{s_2^2}$

Où:

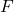$F$ est la statistique de test d’hypothèse pour la variance de deux populations, qui suit une distribution F .
$\sigma_1^2$ est la variance de la population 1.
$\sigma_2^2$ est la variance de la population 2.
$s_1^2$ est la variance de l’échantillon 1.
$s_2^2$ est la variance de l’échantillon 2.
$n_1$ est la taille de l’échantillon 1.
$n_2$ est la taille de l’échantillon 2.

La distribution Snedecor F n’étant pas symétrique, l’hypothèse nulle est rejetée sur la base des critères suivants :

[latex]\begin{array}{l}H_1: \sigma_1^2\neq \sigma_2^2 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } F>F_{1-\alpha/2|n_1-1|n_2-1}\text{ se rechaza } H_0\\[3ex]H_1: \sigma_1^2\neq \sigma_2^2 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si }F \sigma_2^2 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } F>F_{1-\alpha|n_1-1|n_2-1}\text{ se rechaza } H_0\\[3ex]H_1: \sigma_1^2< \sigma_2^2 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } F

à propos de l'auteur

Pr Amélia Rodriguez

En mettant l'accent sur l'apprentissage interactif et les applications pratiques, la professeure Amélia Rodriguez propose des tutoriels complets et des exemples concrets pour rendre les concepts de probabilité accessibles et pertinents pour la vie de ses étudiants. Lire plus