Test de Bartlett pour l’homogénéité des variances (Définition & Exemple)

Le test de Bartlett est un test statistique utilisé pour déterminer si les variances entre plusieurs groupes sont égales ou non.

De nombreux tests statistiques (comme une ANOVA unidirectionnelle ) supposent que les variances sont égales entre les échantillons. Le test de Bartlett peut être utilisé pour vérifier cette hypothèse.

Les étapes suivantes expliquent comment effectuer le test de Bartlett.

Remarque : Ne confondez pas ce test avec le test de sphéricité de Bartlett , qui est utilisé pour comparer une matrice de corrélation observée à la matrice d’identité.

Étapes pour effectuer le test de Bartlett

Le test de Bartlett utilise les hypothèses nulles et alternatives suivantes :

H ₀ : La variance entre chaque groupe est égale.

H _A : Au moins un groupe a une variance qui n’est pas égale aux autres.

La statistique du test peut être calculée comme suit :

B = (nk)lns ² – Σ(n _j -1)lns _j ² / c

où:

• n : le nombre total d’observations dans tous les groupes
• k : Le nombre total de groupes
• ln : Cela signifie « bûche naturelle »
• s ² : La variance poolée
• n _j : Le nombre d’observations dans le groupe j
• s _j ² : La variance du groupe j

Et où c est calculé comme suit :

• c = 1 + (1/3(k-1))*(Σ(1/(n _j -1)) – (1/(nk))

Cette statistique de test suit une distribution du Chi carré avec k-1 degrés de liberté. Autrement dit, B ~ X ² (k-1).

Si la valeur p qui correspond à la statistique du test est inférieure à un certain niveau de signification (comme α = 0,05), nous pouvons alors rejeter l’hypothèse nulle et conclure que tous les groupes n’ont pas la même variance.

Exemple : test de Bartlett

Supposons qu’un professeur veuille savoir si trois techniques d’étude différentes conduisent à des notes moyennes différentes aux examens.

Elle assigne au hasard 10 élèves à utiliser chaque technique pendant une semaine, puis fait passer à chaque élève un examen de difficulté égale.

Les résultats des examens des 30 étudiants sont présentés ci-dessous :

Le professeur souhaite effectuer une ANOVA unidirectionnelle pour voir si les trois techniques conduisent à des résultats moyens différents à l’examen, mais elle doit d’abord effectuer le test de Bartlett pour vérifier que les trois groupes ont des variances égales.

Il est fastidieux d’effectuer le test de Bartlett à la main, nous allons donc saisir les valeurs de données suivantes dans le calculateur de test de Bartlett :

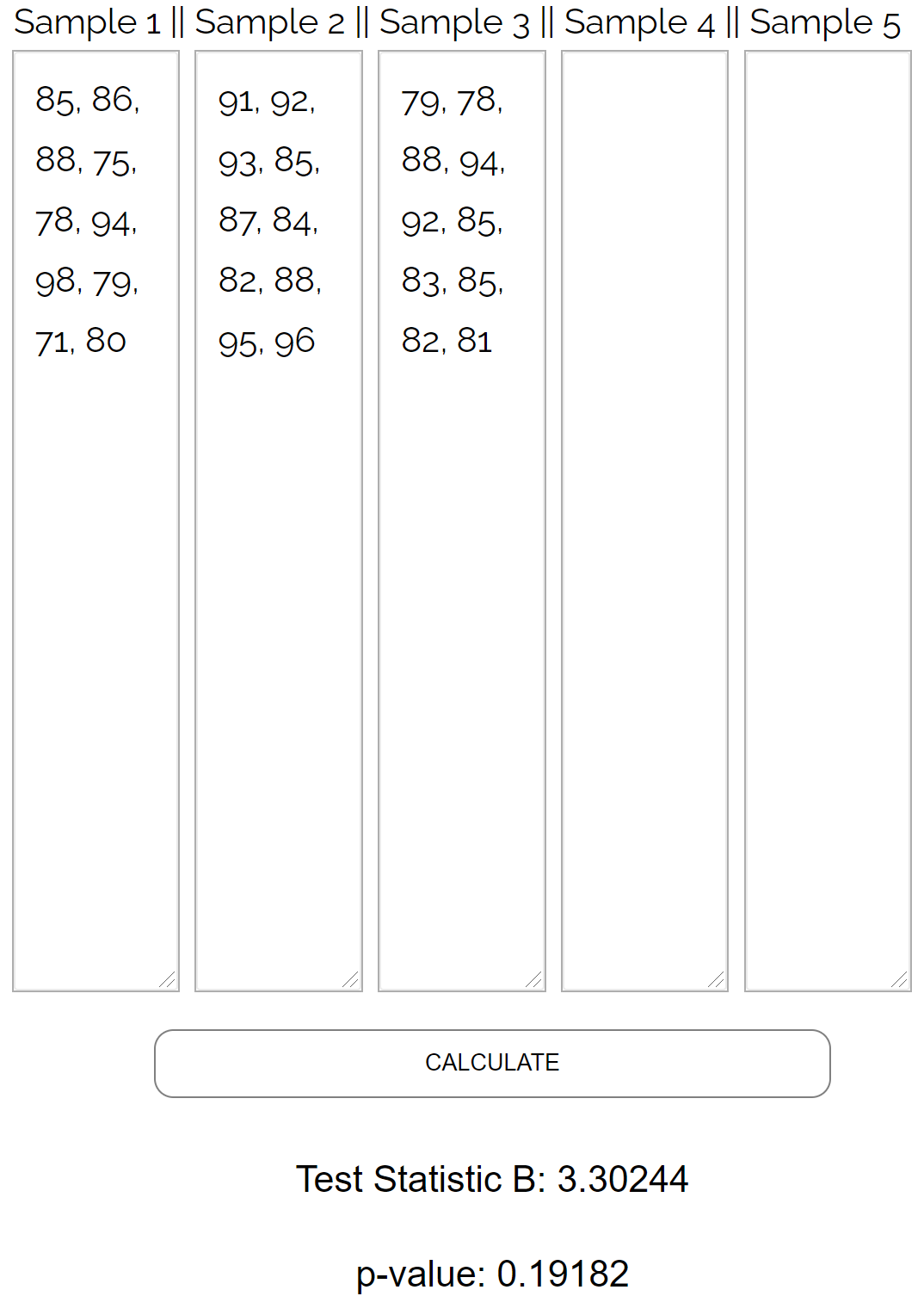
Le test renvoie les résultats suivants :

• Statistique de test B : 3.30244
• Valeur P : 0,19182

Puisque la valeur p n’est pas inférieure à 0,05, le professeur ne parviendra pas à rejeter l’hypothèse nulle. En d’autres termes, elle ne dispose pas de preuves suffisantes pour affirmer que les trois groupes présentent des écarts différents.

Ainsi, elle peut procéder à la réalisation de l’ANOVA unidirectionnelle.

Ressources additionnelles

Comment effectuer le test de Bartlett dans R (étape par étape)
Comment effectuer le test de Bartlett en Python (étape par étape)