Qu’est-ce qu’un test de nourriture ? (Explication & #038; Exemple)

Un test de Chow est un test statistique développé par l’économiste Gregory Chow qui est utilisé pour tester si les coefficients de deux modèles de régression différents sur différents ensembles de données sont égaux.

Le test de Chow est généralement utilisé dans le domaine de l’économétrie avec des données de séries chronologiques pour déterminer s’il existe une rupture structurelle dans les données à un moment donné.

Par exemple, considérons le nuage de points suivant :

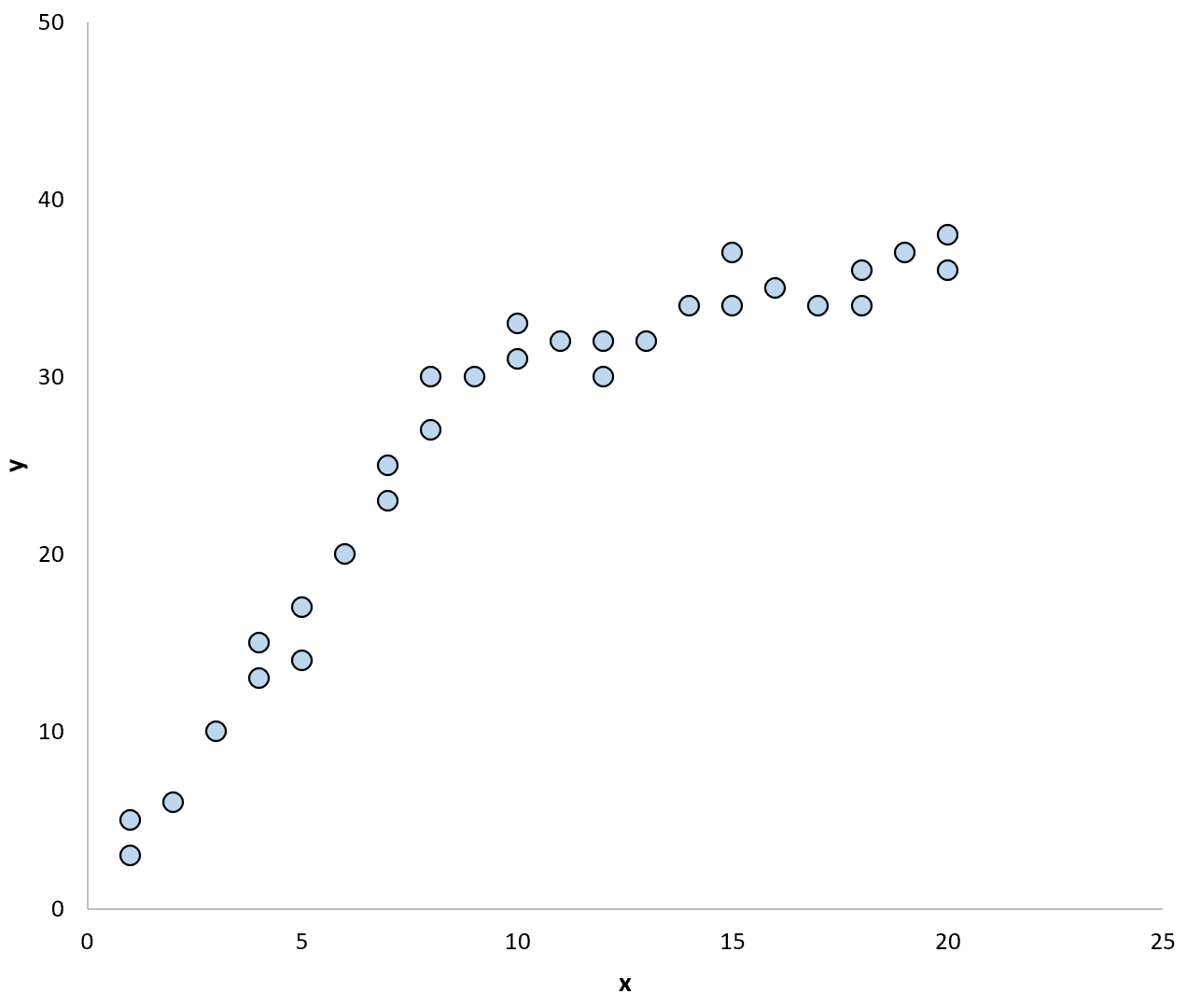
Si nous utilisions une droite de régression pour résumer le modèle dans les données, cela pourrait ressembler à ceci :

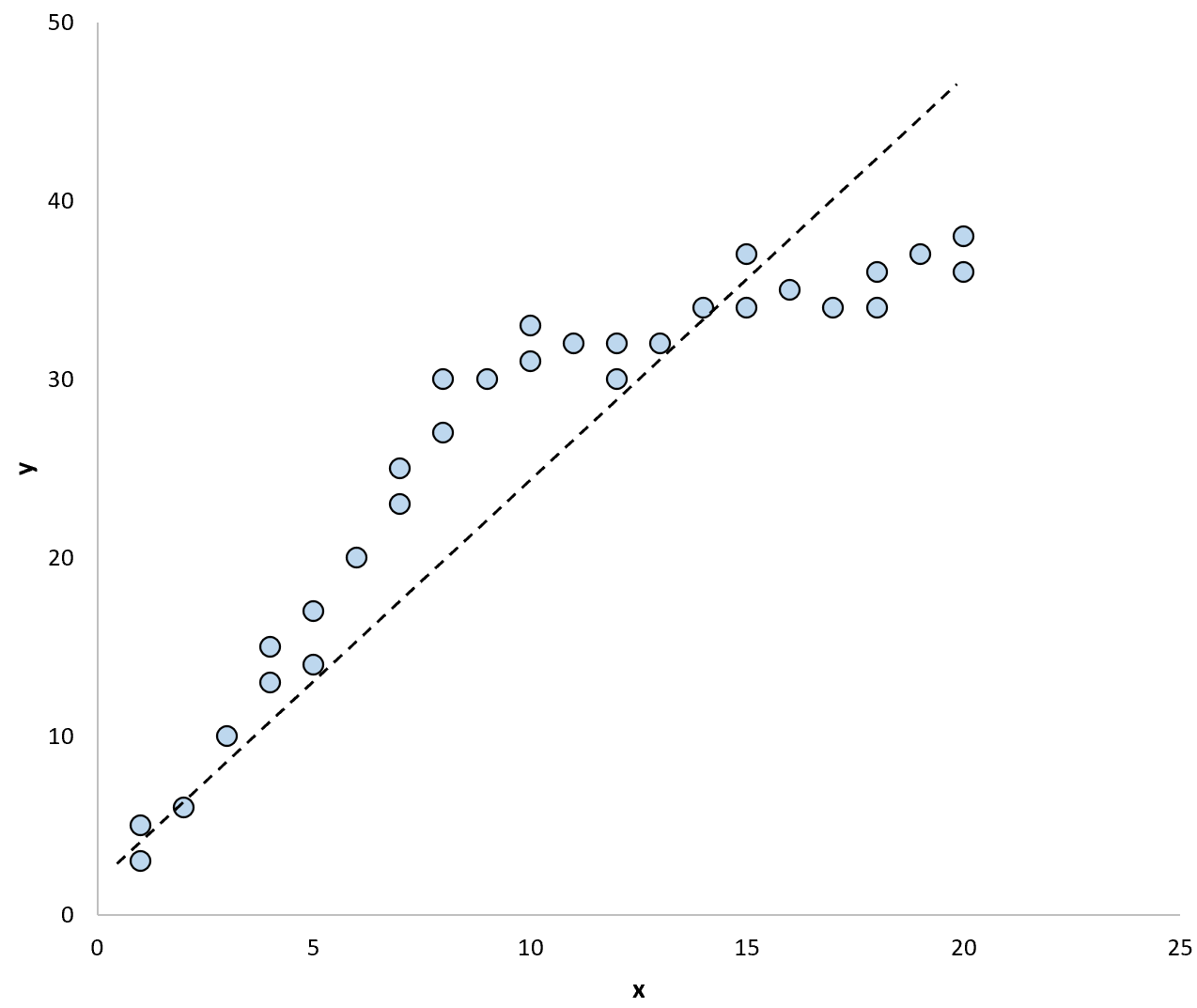
Et si nous utilisions deux droites de régression distinctes pour résumer le modèle dans les données, cela pourrait ressembler à ceci :

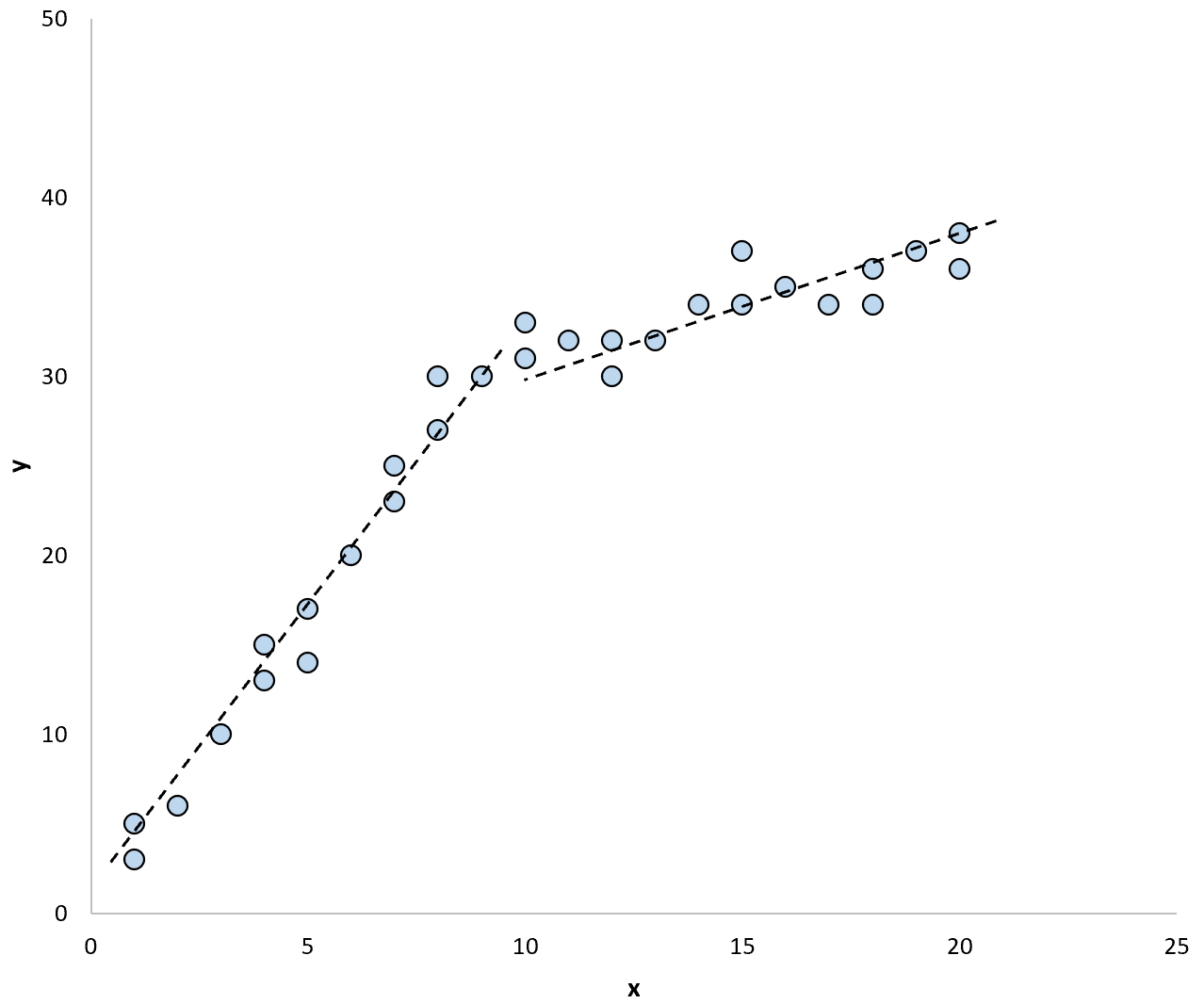
Le test de Chow nous permet de tester si les coefficients de régression de chaque droite de régression sont égaux ou non.

Si le test détermine que les coefficients ne sont pas égaux entre les droites de régression, cela signifie qu’il existe des preuves significatives de l’existence d’une rupture structurelle dans les données. En d’autres termes, la tendance des données est très différente avant et après ce point de rupture structurelle.

Quand utiliser le test Chow

Les exemples suivants illustrent des situations dans lesquelles vous souhaiterez peut-être effectuer un test Chow :

1. Déterminer si les cours des actions évoluent à des taux différents avant et après une élection.

2. Déterminer si les prix des logements changent avant et après un changement de taux d’intérêt.

3. Déterminer si le bénéfice moyen des entreprises publiques est différent avant et après l’adoption d’une nouvelle loi fiscale.

Dans chaque situation, nous pourrions utiliser un test de Chow pour déterminer s’il existe un point de rupture structurelle dans les données à un moment donné.

Étapes pour effectuer un test Chow

Nous pouvons utiliser les étapes suivantes pour effectuer un test Chow.

Étape 1 : Définir les hypothèses nulles et alternatives.

Supposons que nous adaptions le modèle de régression suivant à l’ensemble de notre ensemble de données :

• y _t = a + bx _1t + cx _t2 + ε

Supposons ensuite que nous divisons nos données en deux groupes en fonction d’un point de rupture structurel et que nous ajustions les modèles de régression suivants à chaque groupe :

• y _t = une ₁ + b ₁ x _1t + c ₁ x _t2 + ε
• y _t = une ₂ + b ₂ x _1t + c ₂ x _t2 + ε

Nous utiliserions les hypothèses nulles et alternatives suivantes pour le test de Chow :

• Null (H ₀ ) : a ₁ = a ₂ , b ₁ = b ₂ et c ₁ = c ₂
• Alternative (H _A ) : Au moins une des comparaisons dans Null n’est pas égale.

Si nous rejetons l’hypothèse nulle, nous disposons de preuves suffisantes pour affirmer qu’il existe un point de rupture structurelle dans les données et que deux droites de régression peuvent mieux ajuster les données qu’une.

Si nous ne parvenons pas à rejeter l’hypothèse nulle, nous n’avons pas suffisamment de preuves pour affirmer qu’il existe un point de rupture structurelle dans les données. Dans ce cas, nous disons que les droites de régression peuvent être « regroupées » en une seule droite de régression qui représente suffisamment bien le modèle des données.

Étape 2 : Calculez la statistique du test.

Si l’on définit les termes suivants :

• S _T : La somme des carrés des résidus des données totales
• S ₁ , S ₂ : la somme des carrés des résidus de chaque groupe
• N ₁ , N ₂ : Le nombre d’observations dans chaque groupe
• k : Le nombre de paramètres

Nous pouvons alors dire que la statistique du test de Chow est :

Statistique du test Chow = [(S _T – (S ₁ +S ₂ ))/k] / [(S ₁ +S ₂ )/ (N ₁ +N ₂ -2k)]

Cette statistique de test suit la distribution F avec k et et N ₁ +N ₂ -2k degrés de liberté.

Étape 3 : Rejetez ou ne rejetez pas l’hypothèse nulle.

Si la valeur p associée à cette statistique de test est inférieure à un certain niveau de signification , nous pouvons rejeter l’hypothèse nulle et conclure qu’il existe un point de rupture structurelle dans les données.

Heureusement, la plupart des logiciels statistiques sont capables d’effectuer un test de Chow, vous n’aurez donc probablement jamais à effectuer le test manuellement.

Exemple de réalisation d’un test Chow

Reportez-vous à ce didacticiel pour voir un exemple étape par étape de la façon d’effectuer un test Chow pour un ensemble de données donné dans R.

Notes sur le test Chow

Voici quelques remarques à garder à l’esprit concernant le test Chow :

1. Le test suppose que les résidus des modèles de régression sont distribués indépendamment et de manière identique à partir d’une distribution normale avec une variance inconnue.

2. Le test Chow ne doit être utilisé que lorsque la rupture structurelle que vous souhaitez tester se produit à un moment connu . En d’autres termes, le test ne doit pas être utilisé à plusieurs reprises pour déterminer si un moment donné peut être considéré comme une rupture structurelle.