Comment effectuer un test de corrélation dans Excel (étape par étape)
Une façon de quantifier la relation entre deux variables consiste à utiliser le coefficient de corrélation de Pearson qui est une mesure de l’association linéaire entre deux variables.
Il prend toujours une valeur comprise entre -1 et 1 où :
- -1 indique une corrélation linéaire parfaitement négative entre deux variables
- 0 indique aucune corrélation linéaire entre deux variables
- 1 indique une corrélation linéaire parfaitement positive entre deux variables
Pour déterminer si un coefficient de corrélation est statistiquement significatif, vous pouvez effectuer un test de corrélation, qui consiste à calculer un score t et une valeur p correspondante.
La formule pour calculer le t-score est la suivante :
t = r√ (n-2) / (1-r 2 )
où:
- r : coefficient de corrélation
- n : La taille de l’échantillon
La valeur p est calculée comme la valeur p bilatérale correspondante pour la distribution t avec n-2 degrés de liberté.
L’exemple étape par étape suivant montre comment effectuer un test de corrélation dans Excel.
Étape 1 : Saisissez les données
Commençons par saisir quelques valeurs de données pour deux variables dans Excel :
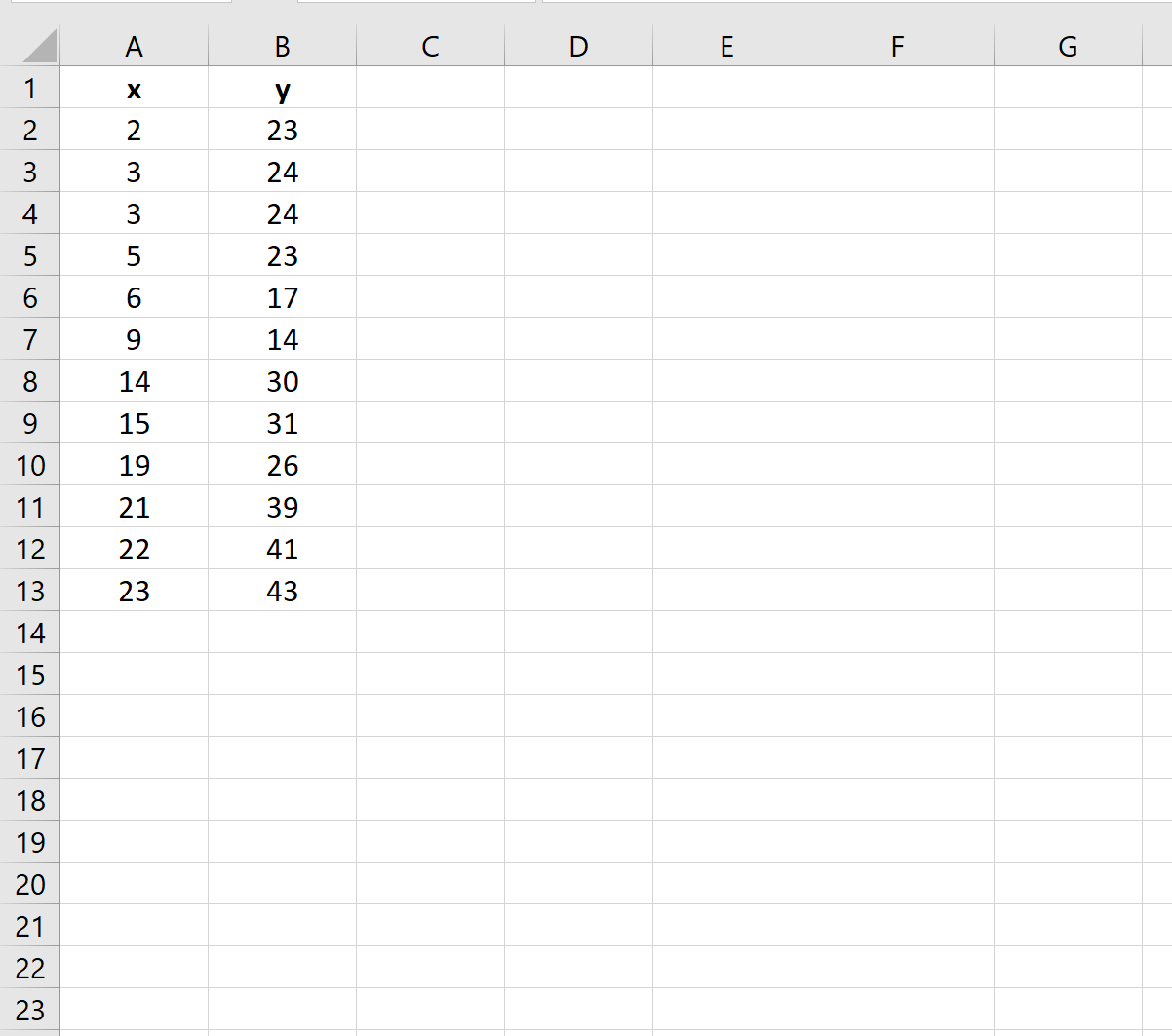
Étape 2 : Calculer le coefficient de corrélation
Ensuite, nous pouvons utiliser la fonction CORREL() pour calculer le coefficient de corrélation entre les deux variables :
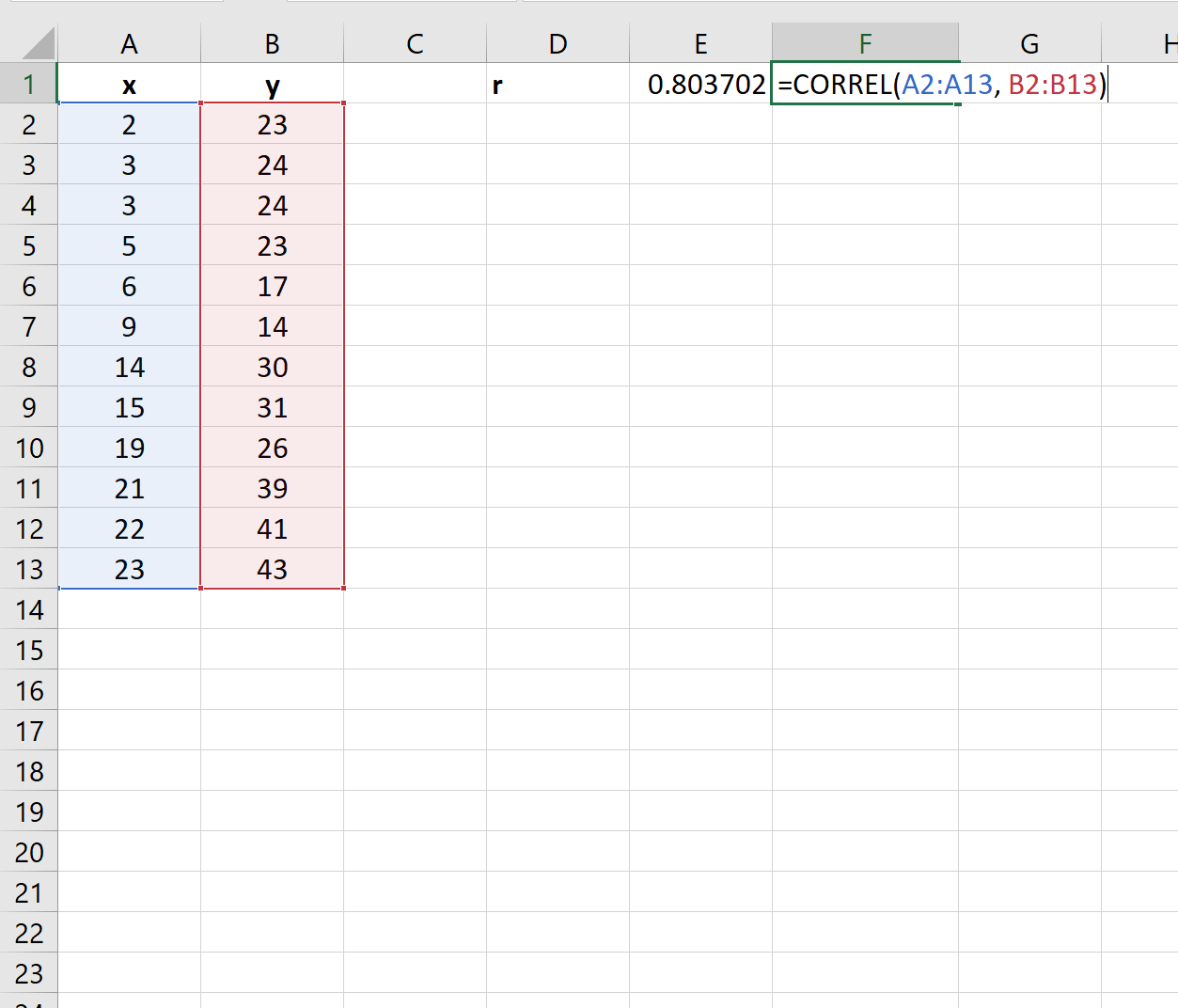
Le coefficient de corrélation entre les deux variables s’avère être de 0,803702 .
Il s’agit d’un coefficient de corrélation très positif, mais pour déterminer s’il est statistiquement significatif, nous devons calculer le score t et la valeur p correspondants.
Étape 3 : Calculer la statistique de test et la valeur P
Ensuite, nous pouvons utiliser les formules suivantes pour calculer la statistique de test et la valeur p correspondante :
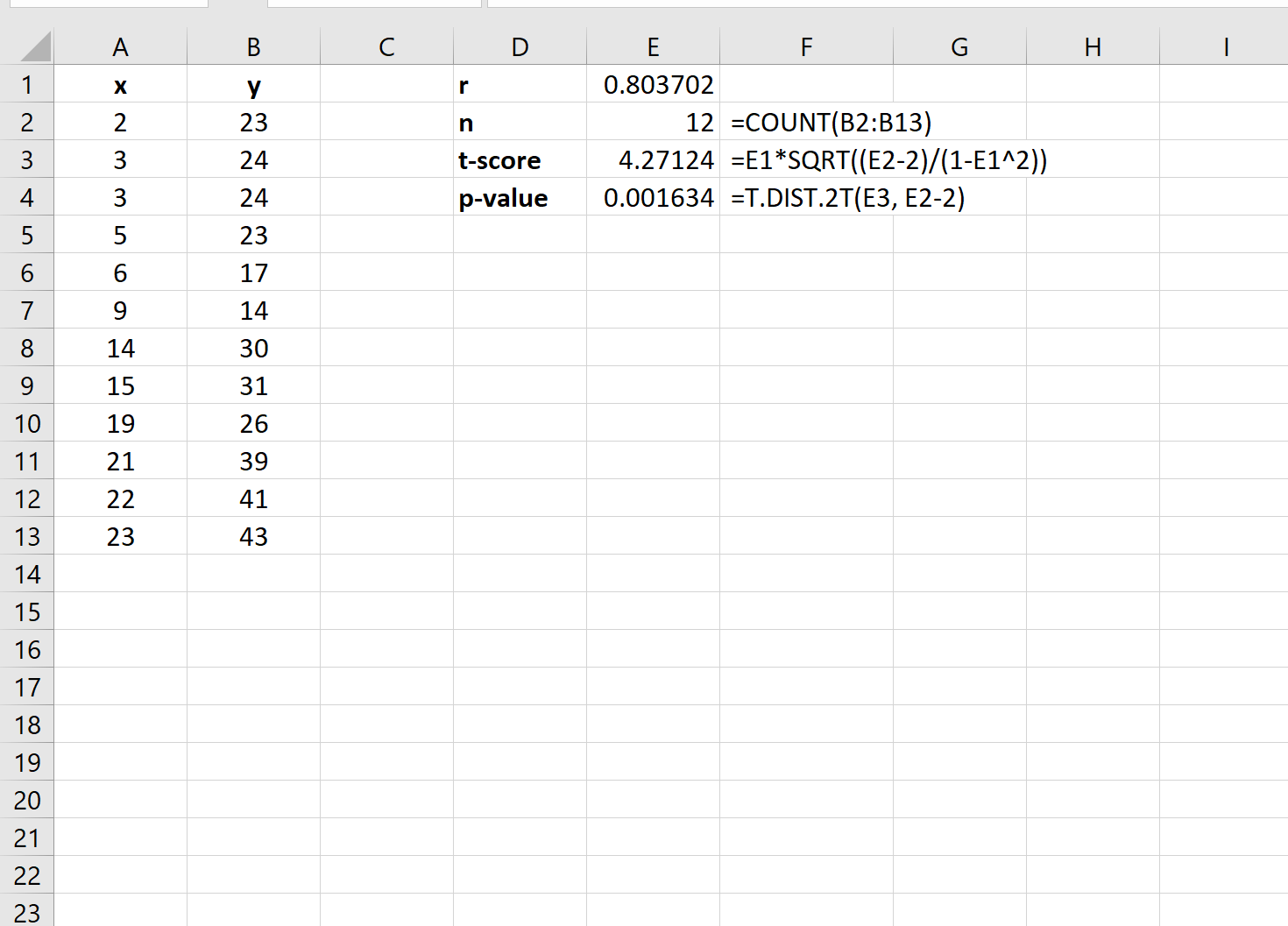
La statistique du test s’avère être 4,27124 et la valeur p correspondante est 0,001634 .
Puisque cette valeur p est inférieure à 0,05, nous disposons de suffisamment de preuves pour affirmer que la corrélation entre les deux variables est statistiquement significative.
Ressources additionnelles
Comment créer une matrice de corrélation dans Excel
Comment calculer la corrélation des classements Spearman dans Excel
Comment calculer la corrélation glissante dans Excel
à propos de l'auteur
Dr. Benjamin Anderson
Il est un professeur de statistiques à la retraite devenu éducateur dévoué sur Statorials. Avec une vaste expérience et une expertise dans le domaine des statistiques, je m'engage à partager mes connaissances pour responsabiliser les étudiants grâce à Statorials. Lire plus