Comment utiliser le test de Dunnett pour des comparaisons multiples

Une ANOVA (Analyse de Variance) est utilisée pour déterminer s’il existe ou non une différence statistiquement significative entre les moyennes de trois groupes indépendants ou plus.

Si la valeur p de l’ANOVA est inférieure à un certain niveau de signification choisi, nous pouvons rejeter l’hypothèse nulle et conclure que nous disposons de preuves suffisantes pour affirmer qu’au moins une des moyennes des groupes est différente des autres.

Cependant, cela ne nous dit pas quels groupes sont différents les uns des autres. Cela nous dit simplement que toutes les moyennes du groupe ne sont pas égales. Afin de savoir exactement quels groupes sont différents les uns des autres, nous devons effectuer un test post-hoc .

Si l’un des groupes de l’étude est considéré comme le groupe témoin , nous devrions alors utiliser le test de Dunnett comme test post-hoc après l’ANOVA.

Test de Dunnett : définition

Nous pouvons utiliser les deux étapes suivantes pour effectuer le test de Dunnett :

Étape 1 : Trouvez la valeur critique de Dunnett.

Premièrement, nous devons trouver la valeur critique de Dunnett. Ceci est calculé comme suit :

Valeur critique de Dunnett : t _d √ 2MS _w /n

où:

• t _d : La valeur trouvée dans le tableau de Dunnett pour un niveau alpha, un nombre de groupes et des tailles d’échantillon de groupe donnés.
• MS _w : Les carrés moyens du « au sein du groupe » dans le tableau de sortie de l’ANOVA
• n : La taille des échantillons de groupe

Étape 2 : Comparez les différences entre les moyennes des groupes à la valeur critique de Dunnett.

Ensuite, nous calculons la différence absolue entre la moyenne de chaque groupe et la moyenne du groupe témoin. Si la différence dépasse la valeur critique de Dunnett, alors cette différence est dite statistiquement significative.

L’exemple suivant montre comment effectuer le test de Dunnett en pratique.

Test de Dunnett : exemple

Supposons qu’un enseignant veuille savoir si deux nouvelles techniques d’étude ont le potentiel d’améliorer les résultats des examens de ses élèves. Pour tester cela, elle divise au hasard sa classe de 30 élèves en trois groupes suivants :

• Groupe témoin : 10 étudiants
• Nouvelle technique d’étude 1 : 10 étudiants
• Nouvelle technique d’étude 2 : 10 étudiants

Après une semaine d’utilisation de la technique d’étude qui lui a été assignée, chaque étudiant passe le même examen. Les résultats sont les suivants:

• Score moyen à l’examen du groupe témoin : 81,6
• Note moyenne à l’examen du groupe nouvelle technique d’étude 1 : 85,8
• Note moyenne à l’examen du groupe Nouvelle technique d’étude 2 : 87,7
• Carrés moyens de « Au sein du groupe » dans le tableau de sortie de l’ANOVA : 23,3

Grâce à ces informations, nous pouvons effectuer le test de Dunnett pour déterminer si l’une des deux nouvelles techniques d’étude produit des résultats moyens aux examens significativement différents de ceux du groupe témoin.

Étape 1 : Trouvez la valeur critique de Dunnett.

En utilisant α = 0,05, la taille de l’échantillon du groupe n = 10 et le total des groupes = 3, le tableau de Dunnett nous indique d’utiliser une valeur de 2,57 dans le calcul de la valeur critique.

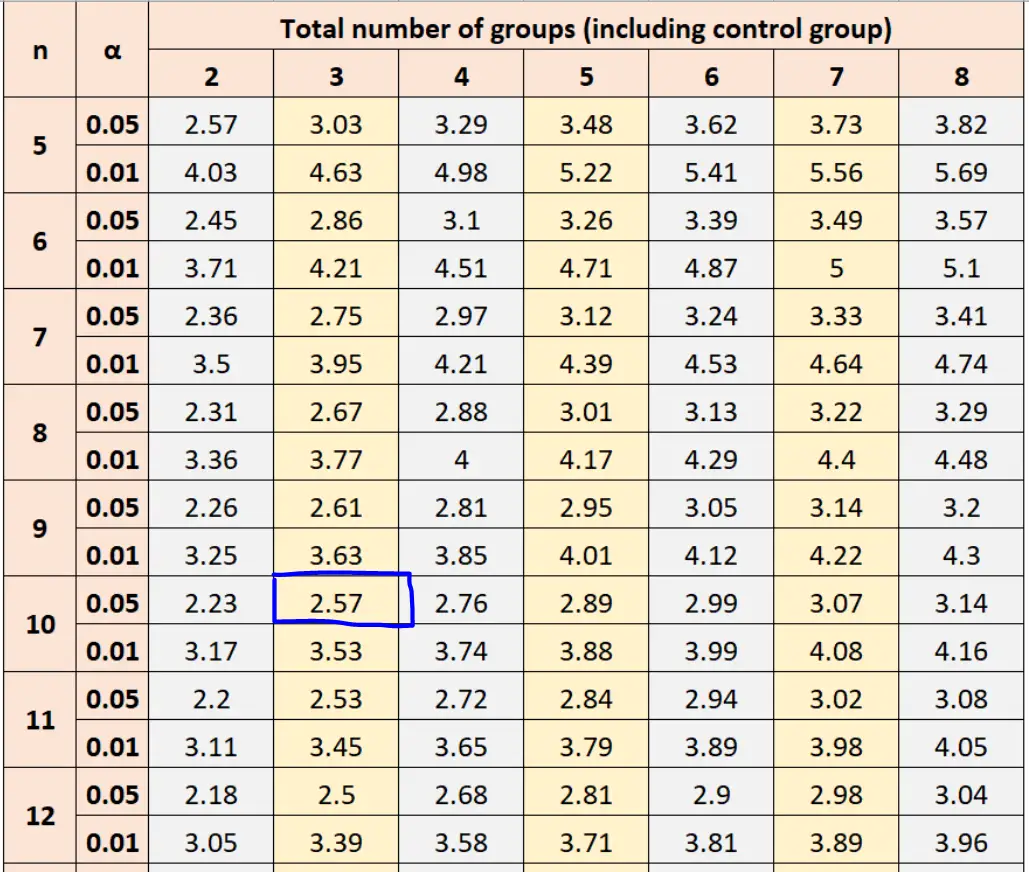
Ensuite, nous pouvons insérer ce nombre dans la formule pour trouver la valeur critique de Dunnett :

Valeur critique de Dunnett : t _d √ 2MS _w /n = 2,57√ 2(23,3)/10 = 5,548

Étape 2 : Comparez les différences entre les moyennes des groupes à la valeur critique de Dunnett.

Les différences absolues entre les moyennes de chaque technique d’étude et celles du groupe témoin sont les suivantes :

• Abdos. diff entre la nouvelle technique 1 et le contrôle : |85,8 – 81,6| = 4,2
• Abdos. diff entre la nouvelle technique 2 et le contrôle : |87,7 – 81,6| = 6,1

Seule la différence absolue entre la technique 2 et le groupe témoin est supérieure à la valeur critique de Dunnett de 5,548 .

Ainsi, nous pouvons dire que la nouvelle technique d’étude n°2 produit des résultats d’examen significativement différents par rapport au groupe témoin, mais ce n’est pas le cas de la nouvelle technique d’étude n°1.

Ressources additionnelles

Une introduction à l’ANOVA unidirectionnelle
Un guide d’utilisation des tests post-hoc avec ANOVA
Comment effectuer le test de Dunnett dans R