Comment effectuer un test de normalité dans Excel (étape par étape)
De nombreux tests statistiques supposent que les valeurs d’un ensemble de données sont normalement distribuées .
L’un des moyens les plus simples de tester cette hypothèse consiste à effectuer un test de Jarque-Bera , qui est un test d’ajustement qui détermine si les données d’échantillon présentent ou non une asymétrie et un aplatissement correspondant à une distribution normale.
Ce test utilise les hypothèses suivantes :
H 0 : Les données sont normalement distribuées.
H A : Les données ne sont pas normalement distribuées.
La statistique de test JB est définie comme :
JB =(n/6) * (S 2 + (C 2 /4))
où:
- n : le nombre d’ observations dans l’échantillon
- S : l’asymétrie de l’échantillon
- C : l’échantillon d’aplatissement
Sous l’hypothèse nulle de normalité, JB ~ X 2 (2).
Si la valeur p qui correspond à la statistique de test est inférieure à un certain niveau de signification (par exemple α = 0,05), alors nous pouvons rejeter l’hypothèse nulle et conclure que les données ne sont pas distribuées normalement.
Ce didacticiel fournit un exemple étape par étape de la façon d’effectuer un test Jarque-Bera pour un ensemble de données donné dans Excel.
Étape 1 : Créer les données
Tout d’abord, créons un faux ensemble de données avec 15 valeurs :
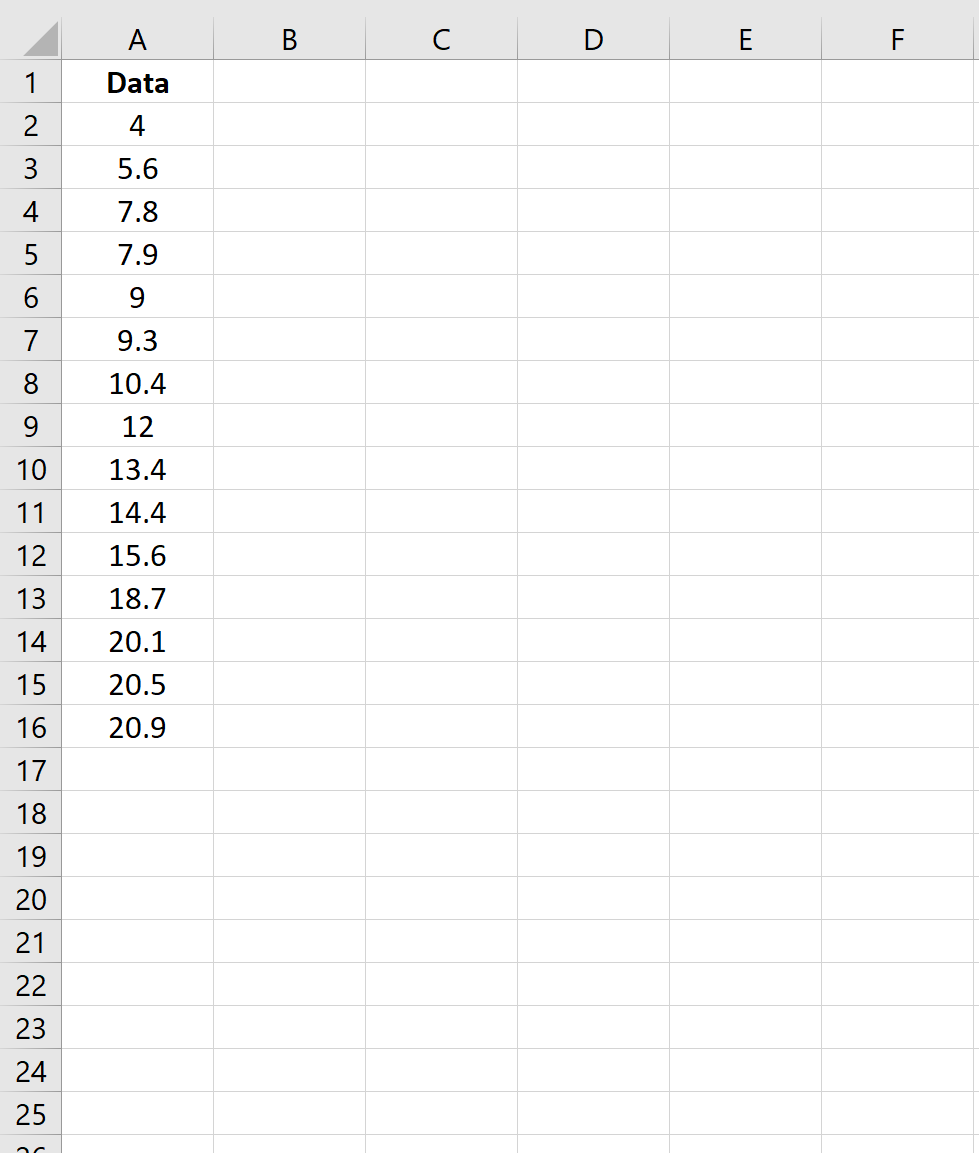
Étape 2 : Calculer la statistique du test
Ensuite, calculez la statistique du test JB. La colonne E montre les formules utilisées :
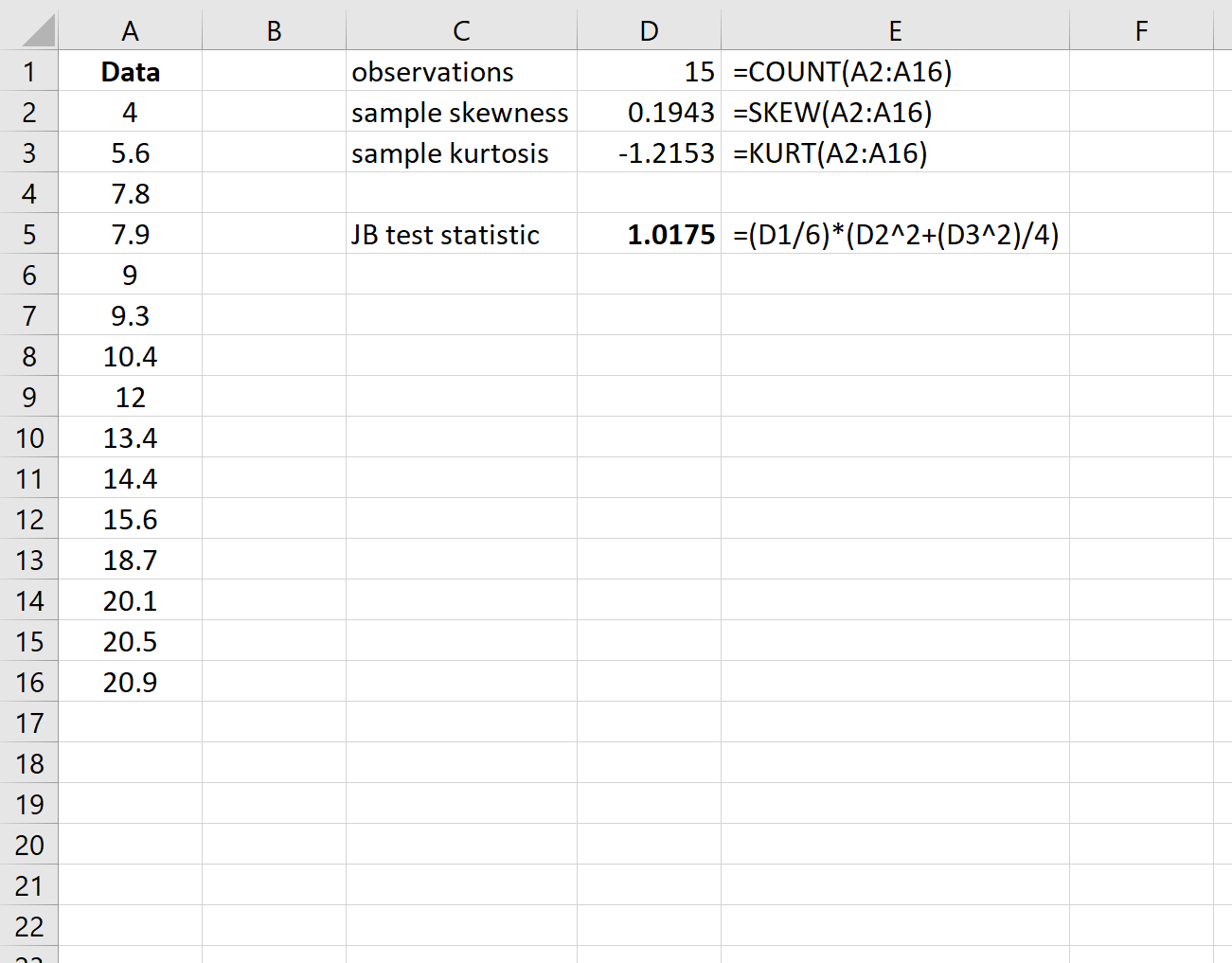
La statistique du test s’avère être 1,0175 .
Étape 3 : Calculer la valeur P
Sous l’hypothèse nulle de normalité, la statistique de test JB suit une distribution du Chi carré à 2 degrés de liberté.
Ainsi, pour trouver la valeur p pour le test, nous utiliserons la fonction suivante dans Excel : =CHISQ.DIST.RT(Statistique du test JB, 2)
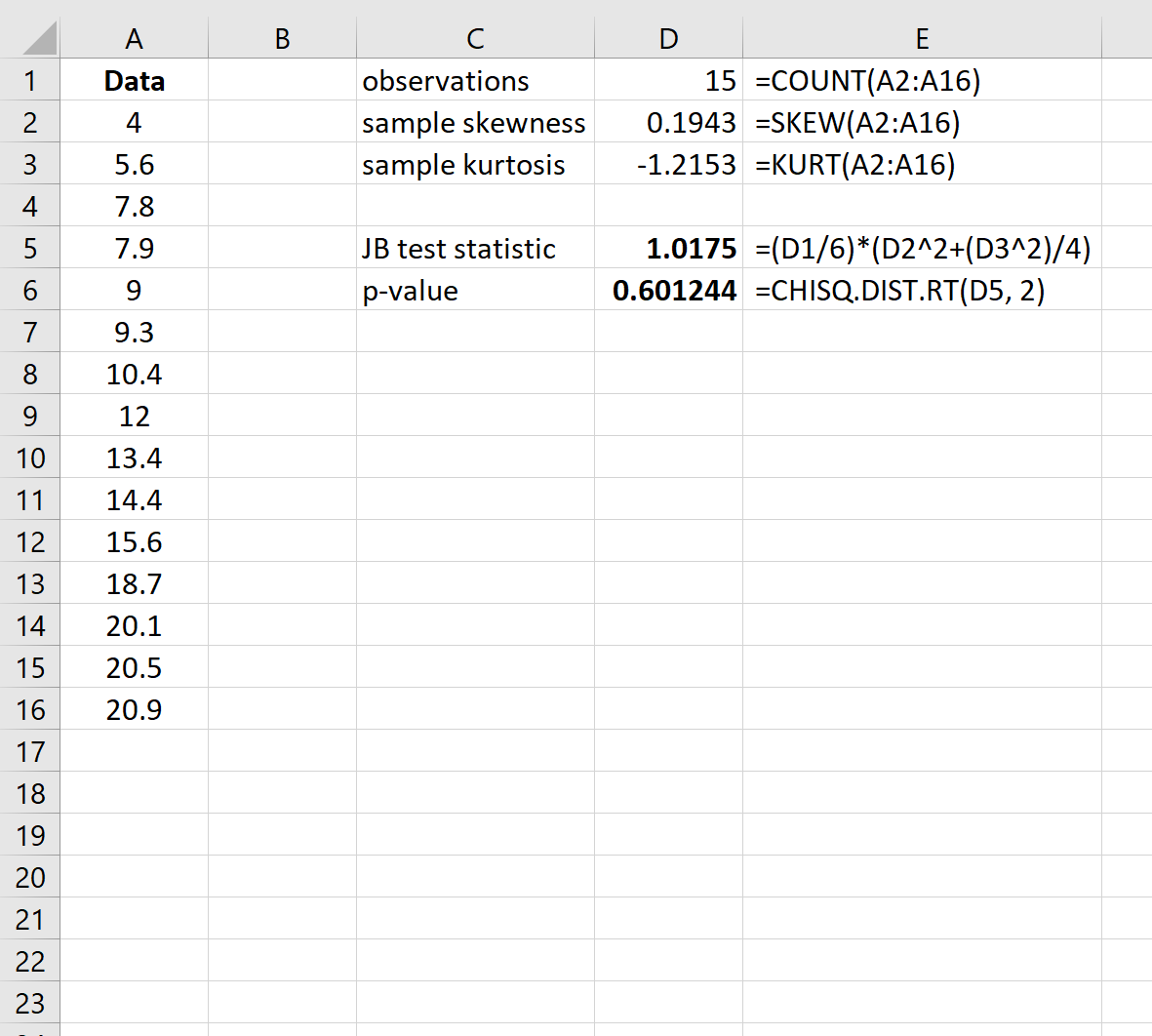
La valeur p du test est de 0,601244 . Puisque cette valeur p n’est pas inférieure à 0,05, nous ne parvenons pas à rejeter l’hypothèse nulle. Nous n’avons pas suffisamment de preuves pour affirmer que l’ensemble de données n’est pas normalement distribué.
En d’autres termes, on peut supposer que les données sont normalement distribuées.
Ressources additionnelles
Comment créer un tracé QQ dans Excel
Comment effectuer un test d’ajustement du chi carré dans Excel
à propos de l'auteur
Dr. Benjamin Anderson
Il est un professeur de statistiques à la retraite devenu éducateur dévoué sur Statorials. Avec une vaste expérience et une expertise dans le domaine des statistiques, je m'engage à partager mes connaissances pour responsabiliser les étudiants grâce à Statorials. Lire plus