Test d’hypothèse pour la différence de moyennes
Cet article explique ce qu’est le test d’hypothèse sur la différence de moyennes dans les statistiques et à quoi il sert. De même, vous découvrirez comment faire un test d’hypothèse sur la différence de moyennes et un exercice résolu étape par étape.
Qu’est-ce que le test d’hypothèse pour la différence moyenne ?
Le test d’hypothèse pour la différence de moyennes est un test statistique utilisé pour rejeter ou accepter l’hypothèse selon laquelle les moyennes de deux populations sont différentes. Autrement dit, le test d’hypothèse sur la différence de moyennes est utilisé pour déterminer si les moyennes de deux populations sont identiques ou différentes.
Gardez à l’esprit que les décisions prises dans les tests d’hypothèse sont basées sur un niveau de confiance préalablement établi, on ne peut donc pas garantir que le résultat d’un test d’hypothèse est toujours correct, mais plutôt que c’est le résultat le plus probable qui est vrai.
Le test d’hypothèse pour la différence de deux moyennes consiste à calculer la statistique du test et à la comparer à la valeur critique pour rejeter ou non l’hypothèse nulle. Ci-dessous, nous verrons comment effectuer un test d’hypothèse pour la différence de moyennes.
Enfin, rappelez-vous qu’en statistique, les tests d’hypothèses peuvent également être appelés contrastes d’hypothèses, tests d’hypothèses ou tests de signification.
Formule de test d’hypothèse pour la différence de moyennes
La formule qui doit être utilisée pour tester les hypothèses sur la différence des moyennes varie selon que les variances de la population sont connues et, dans le cas contraire, si elles peuvent être supposées identiques ou différentes. Ainsi, dans cette section, nous verrons quelle formule utiliser selon les cas.
Variations connues
La formule de calcul de la statistique du test d’hypothèse pour la différence des moyennes lorsque les variances sont connues est la suivante :

Où:
 est la statistique de test d’hypothèse pour la différence de deux moyennes avec une variance connue, qui suit une distribution normale standard.
est la statistique de test d’hypothèse pour la différence de deux moyennes avec une variance connue, qui suit une distribution normale standard. est la moyenne de la population 1.
est la moyenne de la population 1. est la moyenne de la population 2.
est la moyenne de la population 2. est la moyenne de l’échantillon 1.
est la moyenne de l’échantillon 1. est la moyenne de l’échantillon 2.
est la moyenne de l’échantillon 2. est l’écart type de la population 1.
est l’écart type de la population 1. est l’écart type de la population 2.
est l’écart type de la population 2. est la taille de l’échantillon 1.
est la taille de l’échantillon 1. est la taille de l’échantillon 2.
est la taille de l’échantillon 2.
Gardez à l’esprit qu’il s’agit du cas le moins courant, cette formule n’est donc utilisée que dans certains cas spécifiques.
Écarts inconnus et égaux
La formule permettant de calculer la statistique du test d’hypothèse pour la différence des moyennes lorsque les variances de la population sont inconnues mais supposées égales est la suivante :

Où:
 est la statistique de test d’hypothèse pour la différence de moyennes avec des variances inconnues, qui suit une distribution t de Student avec n 1 + n 2 -2 degrés de liberté.
est la statistique de test d’hypothèse pour la différence de moyennes avec des variances inconnues, qui suit une distribution t de Student avec n 1 + n 2 -2 degrés de liberté. est la moyenne de la population 1.
est la moyenne de la population 1. est la moyenne de la population 2.
est la moyenne de la population 2. est la moyenne de l’échantillon 1.
est la moyenne de l’échantillon 1. est la moyenne de l’échantillon 2.
est la moyenne de l’échantillon 2. est l’écart type combiné.
est l’écart type combiné. est la taille de l’échantillon 1.
est la taille de l’échantillon 1. est la taille de l’échantillon 2.
est la taille de l’échantillon 2.
L’écart type combiné des deux échantillons est calculé avec la formule suivante :

Variations inconnues et différentes
Lorsque les variances des populations sont inconnues et, en outre, elles sont supposées différentes, la formule pour calculer la statistique du test d’hypothèse pour la différence des moyennes est la suivante :

Où:
 est la statistique de test d’hypothèse pour la différence de moyennes avec des variances inconnues, qui suit la distribution t de Student.
est la statistique de test d’hypothèse pour la différence de moyennes avec des variances inconnues, qui suit la distribution t de Student. est la moyenne de la population 1.
est la moyenne de la population 1. est la moyenne de la population 2.
est la moyenne de la population 2. est la moyenne de l’échantillon 1.
est la moyenne de l’échantillon 1. est la moyenne de l’échantillon 2.
est la moyenne de l’échantillon 2. est l’écart type de la population 1.
est l’écart type de la population 1. est l’écart type de la population 2.
est l’écart type de la population 2. est la taille de l’échantillon 1.
est la taille de l’échantillon 1. est la taille de l’échantillon 2.
est la taille de l’échantillon 2.
Cependant, dans ce cas, les degrés de liberté de la distribution t de Student sont calculés à l’aide de la formule suivante :

Exemple concret du test d’hypothèse pour la différence de moyennes
Pour finir d’assimiler le concept de test d’hypothèse sur la différence de moyennes, nous allons voir un exemple concret de ce type de test d’hypothèse.
- Vous souhaitez faire une étude statistique sur le salaire de deux entreprises concurrentes, plus précisément, vous souhaitez déterminer si le salaire moyen des deux entreprises est différent. Pour ce faire, un échantillon de 47 travailleurs d’une entreprise et un autre échantillon de 55 travailleurs de l’autre entreprise sont prélevés. Un salaire moyen de 40 000 $ et un écart type de 12 000 $ sont obtenus à partir du premier échantillon, tandis qu’un salaire moyen de 46 000 $ et un écart type de 18 000 $ sont obtenus à partir du deuxième échantillon. Effectuez un test d’hypothèse avec un niveau de signification de 5 % pour déterminer si les salaires moyens sont différents ou non.
Dans ce cas, l’hypothèse nulle et l’hypothèse alternative du test d’hypothèse pour la différence des deux moyennes sont les suivantes :
![Rendered by QuickLaTeX.com \begin{cases}H_0: \mu_1-\mu_2=0\\[2ex] H_1:\mu_1-\mu_2\neq 0 \end{cases}](https://statorials.org/wp-content/ql-cache/quicklatex.com-4dd9e80c0a87987d689d7b8d99be9d90_l3.png)
Dans ce cas, les écarts des populations ne sont pas connus, mais on peut supposer qu’elles sont égales car ce sont des entreprises concurrentes et les conditions de travail du marché dans lequel elles opèrent sont très similaires. Par conséquent, la formule pour la statistique de test d’hypothèse pour la différence de moyennes que nous devons utiliser est la suivante :

Nous calculons donc l’écart type poolé des deux échantillons :
![Rendered by QuickLaTeX.com \begin{aligned}\displaystyle s_p&=\sqrt{\frac{(n_1-1)s_1^2+(n_2-1)s_2^2}{n_1+n_2-2}}\\[2ex]\displaystyle s_p&=\sqrt{\frac{(47-1)\cdot 12000^2+(55-1)\cdot 18000^2}{47+55-2}}\\[2ex]s_p&=15530,61\end{aligned}](https://statorials.org/wp-content/ql-cache/quicklatex.com-0308363d68c4677761d44b214b1609d9_l3.png)
Nous appliquons maintenant la formule du test d’hypothèse pour la différence de moyennes :
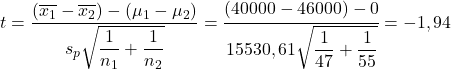
En revanche, on recherche la valeur critique du test d’hypothèse pour la différence de moyennes dans le tableau t de Student :
![]()
![Rendered by QuickLaTeX.com \begin{array}{c}t_{\alpha/2| n_1+n_2-2}= \ \color{orange}\bm{?}\\[4ex]t_{0,025| 100}=1,984\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-d5f11ecd0336e50c63b0ab2fab4bd530_l3.png)
Ensuite, puisque la valeur absolue de la statistique du test est inférieure à la valeur critique du test, l’hypothèse nulle est acceptée et l’hypothèse alternative est rejetée.
![]()
