Test d’hypothèse pour la moyenne
Cet article explique ce qu’est un test d’hypothèse pour la moyenne en statistique. Ainsi, vous trouverez la formule du test d’hypothèse pour la moyenne et, en complément, un exercice résolu étape par étape.
Qu’est-ce que le test d’hypothèse pour la moyenne ?
Le test d’hypothèse pour la moyenne est une méthode statistique utilisée pour rejeter ou rejeter l’hypothèse nulle d’une moyenne de population.
Plus précisément, le test d’hypothèse pour la moyenne consiste à calculer la statistique du test et à la comparer à la valeur critique pour rejeter ou non l’hypothèse nulle.
Il convient de noter que les tests d’hypothèse portent des noms différents ; en statistique, ils sont également appelés contrastes d’hypothèses, tests d’hypothèse ou tests de signification.
Formule de test d’hypothèse pour la moyenne
Nous verrons ensuite comment la statistique du test d’hypothèse pour la moyenne est calculée. Cependant, la formule varie légèrement selon que la variance est connue ou non, nous verrons donc d’abord comment cela se fait lorsque la variance est connue puis lorsque la variance est inconnue.
Avec écart connu
La formule de test d’hypothèse pour la moyenne avec une variance connue est la suivante :

Où:
 est la statistique du test d’hypothèse pour la moyenne.
est la statistique du test d’hypothèse pour la moyenne. est la moyenne de l’échantillon.
est la moyenne de l’échantillon. est la valeur moyenne proposée.
est la valeur moyenne proposée. est l’écart type de la population.
est l’écart type de la population. est la taille de l’échantillon.
est la taille de l’échantillon.
Une fois la statistique du test d’hypothèse pour la moyenne calculée, le résultat doit être interprété pour rejeter ou rejeter l’hypothèse nulle :
- Si le test d’hypothèse pour la moyenne est bilatéral, l’hypothèse nulle est rejetée si la valeur absolue de la statistique est supérieure à la valeur critique Z α/2 .
- Si le test d’hypothèse pour la moyenne correspond à la queue droite, l’hypothèse nulle est rejetée si la statistique est supérieure à la valeur critique Z α .
- Si le test d’hypothèse pour la moyenne correspond à la queue gauche, l’hypothèse nulle est rejetée si la statistique est inférieure à la valeur critique -Z α .
![Rendered by QuickLaTeX.com \begin{array}{l}H_1: \mu\neq \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } |Z|>Z_{\alpha/2} \text{ se rechaza } H_0\\[3ex]H_1: \mu> \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } Z>Z_{\alpha} \text{ se rechaza } H_0\\[3ex]H_1: \mu< \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } Z<-Z_{\alpha} \text{ se rechaza } H_0\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-0e2ccadfc369eb7543b8f86dfccc528e_l3.png)
Dans ce cas, les valeurs critiques sont obtenues à partir du tableau de distribution normale standardisé .
Avec une variance inconnue
La formule de test d’hypothèse pour la moyenne avec une variance inconnue est la suivante :

Où:
 est la statistique de test d’hypothèse pour la moyenne, qui est définie par une distribution t de Student .
est la statistique de test d’hypothèse pour la moyenne, qui est définie par une distribution t de Student . est la moyenne de l’échantillon.
est la moyenne de l’échantillon. est la valeur moyenne proposée.
est la valeur moyenne proposée. est l’écart type de l’échantillon.
est l’écart type de l’échantillon. est la taille de l’échantillon.
est la taille de l’échantillon.
Comme précédemment, le résultat calculé de la statistique de test doit être interprété avec la valeur critique pour rejeter ou non l’hypothèse nulle :
- Si le test d’hypothèse pour la moyenne est bilatéral, l’hypothèse nulle est rejetée si la valeur absolue de la statistique est supérieure à la valeur critique t α/2|n-1 .
- Si le test d’hypothèse pour la moyenne correspond à la queue droite, l’hypothèse nulle est rejetée si la statistique est supérieure à la valeur critique t α|n-1 .
- Si le test d’hypothèse pour la moyenne correspond à la queue gauche, l’hypothèse nulle est rejetée si la statistique est inférieure à la valeur critique -t α|n-1 .
![Rendered by QuickLaTeX.com \begin{array}{l}H_1: \mu\neq \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } |t|>t_{\alpha/2|n-1} \text{ se rechaza } H_0\\[3ex]H_1: \mu> \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } t>t_{\alpha|n-1} \text{ se rechaza } H_0\\[3ex]H_1: \mu< \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } t<-t_{\alpha|n-1} \text{ se rechaza } H_0\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-31fb206b75a47181c7c673f54ba28ee8_l3.png)
Lorsque la variance est inconnue, les valeurs critiques du test sont obtenues à partir de la table de distribution t de Student.
Exemple concret du test d’hypothèse pour la moyenne
Pour bien comprendre le concept de test d’hypothèse pour la moyenne de la population, vous pouvez voir ci-dessous un exemple concret de ce type de test d’hypothèse.
- Une entreprise technologique affirme que la batterie de l’ordinateur portable qu’elle vend dure 6 heures. Nous vérifions si cette hypothèse est fausse en effectuant un test d’hypothèse avec un niveau de signification α = 0,05. Pour ce faire, il est décidé d’acheter 20 unités et d’observer la durée de vie de la batterie de chaque ordinateur (les valeurs sont exprimées en heures) :
5,2 5,9 7,1 4,2 6,5
8,5 4,6 6,8 6,9 5,8
5,1 6,5 7,0 5,3 6,2
5,7 6,6 7,5 5,1 6,1
Dans ce cas, les hypothèses nulles et alternatives du test d’hypothèse sur la moyenne sont les suivantes :
![Rendered by QuickLaTeX.com \begin{cases}H_0: \mu=6\\[2ex] H_1:\mu\neq 6 \end{cases}](https://statorials.org/wp-content/ql-cache/quicklatex.com-329ffe392783b8bee1eef642d1a45f53_l3.png)
Afin de déterminer la statistique du test, nous devons d’abord calculer la moyenne de l’échantillon et l’écart type de l’échantillon :
![]()
Puisque nous ne connaissons pas la variance de la population, pour obtenir la statistique de test, nous devons appliquer la formule de test d’hypothèse pour la moyenne avec une variance inconnue :

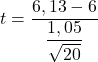
![]()
Nous devons maintenant trouver la valeur critique du test d’hypothèse, nous cherchons donc dans le tableau de distribution t de Student la valeur correspondante. Les degrés de liberté du t de Student sont inférieurs de un à la taille de l’échantillon (20-1=19) et, d’autre part, la probabilité correspondante est la moitié du niveau de signification (0,05/2=0,025) puisqu’il s’agit d’un deux- test d’hypothèse face.
![]()
![Rendered by QuickLaTeX.com \begin{array}{c}t_{\alpha/2| n-1}= \ \color{orange}\bm{?}\\[4ex]t_{0,025| 19}=2,093\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-e85692dfb2fb2522025566dc205b8117_l3.png)
En conclusion, puisqu’il s’agit d’un test d’hypothèse bilatéral et que la valeur absolue de la statistique du test est inférieure à la valeur critique, l’hypothèse nulle n’est pas rejetée, mais l’hypothèse alternative est rejetée.
![]()
Test d’hypothèse pour la différence de moyennes
Le test d’hypothèse sur la différence de moyennes est utilisé pour rejeter ou accepter l’hypothèse nulle selon laquelle les moyennes de deux populations sont identiques.
Ainsi l’hypothèse nulle d’un test d’hypothèse pour la différence de deux moyennes est toujours la suivante :
![]()
Alors que l’hypothèse alternative peut être l’une des trois suivantes :
![Rendered by QuickLaTeX.com \begin{array}{l}H_1:\mu_1\neq \mu_2\\[2ex]H_1:\mu_1>\mu_2\\[2ex]H_1:\mu_1<\mu_2\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-c612ac7651faad9faa195f37fdf6edef_l3.png)
Ensuite, la formule pour calculer la statistique du test d’hypothèse pour la différence des moyennes lorsque la variance est connue est la suivante :
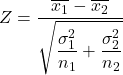
Où:
 est la statistique de test d’hypothèse pour la différence de deux moyennes avec une variance connue, qui suit une distribution normale standard.
est la statistique de test d’hypothèse pour la différence de deux moyennes avec une variance connue, qui suit une distribution normale standard. est la moyenne de l’échantillon 1.
est la moyenne de l’échantillon 1. est la moyenne de l’échantillon 2.
est la moyenne de l’échantillon 2. est la variance de la population 1.
est la variance de la population 1. est la variance de la population 2.
est la variance de la population 2. est la taille de l’échantillon 1.
est la taille de l’échantillon 1. est la taille de l’échantillon 2.
est la taille de l’échantillon 2.
D’autre part, la formule pour calculer la statistique du test d’hypothèse pour la différence des moyennes lorsque la variance est inconnue est la suivante :
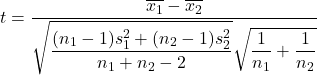
Où:
 est la statistique de test d’hypothèse pour la différence de deux moyennes avec une variance inconnue, qui suit la distribution t de Student.
est la statistique de test d’hypothèse pour la différence de deux moyennes avec une variance inconnue, qui suit la distribution t de Student. est la moyenne de l’échantillon 1.
est la moyenne de l’échantillon 1. est la moyenne de l’échantillon 2.
est la moyenne de l’échantillon 2. est la variance de l’échantillon 1.
est la variance de l’échantillon 1. est la variance de l’échantillon 2.
est la variance de l’échantillon 2. est la taille de l’échantillon 1.
est la taille de l’échantillon 1. est la taille de l’échantillon 2.
est la taille de l’échantillon 2.
