Test d’hypothèse pour la proportion

Par Pr Amélia Rodriguez août 3, 2023 Statistiques 0 commentaire

Cet article explique ce qu’est le test d’hypothèse de proportion dans les statistiques. Vous trouverez donc la formule du test d’hypothèse pour la proportion et, en complément, un exercice pas à pas pour bien comprendre comment cela se fait.

Qu’est-ce qu’un test d’hypothèse pour la proportion ?

Le test d’hypothèse de proportion est une méthode statistique utilisée pour déterminer s’il faut ou non rejeter l’hypothèse nulle d’une proportion de population.

Ainsi, selon la valeur de la statistique du test d’hypothèse pour la proportion et le niveau de signification, l’hypothèse nulle est rejetée ou acceptée.

Notez que les tests d’hypothèse peuvent également être appelés contrastes d’hypothèses, tests d’hypothèse ou tests de signification.

Formule de test d’hypothèse pour la proportion

La statistique du test d’hypothèse pour la proportion est égale à la différence de la proportion de l’échantillon moins la valeur proposée de la proportion divisée par l’écart type de la proportion.

La formule de test d’hypothèse pour la proportion est donc la suivante :

$\displaystyle Z=\frac{\widehat{p}-p}{\displaystyle\sqrt{\frac{p(1-p)}{n}}}$

Où:

$Z$ est la statistique du test d’hypothèse pour la proportion.
$\widehat{p}$ est la proportion de l’échantillon.
$p$ est la valeur de la proportion proposée.
$n$ est la taille de l’échantillon.
$\displaystyle\sqrt{\frac{p(1-p)}{n}}$ est l’écart type de la proportion.

Gardez à l’esprit qu’il ne suffit pas de calculer la statistique du test d’hypothèse pour la proportion, mais le résultat doit ensuite être interprété :

Si le test d’hypothèse pour la proportion est bilatéral, l’hypothèse nulle est rejetée si la valeur absolue de la statistique est supérieure à la valeur critique Z _α/2 .
Si le test d’hypothèse pour la proportion correspond à la queue droite, l’hypothèse nulle est rejetée si la statistique est supérieure à la valeur critique Z _α .
Si le test d’hypothèse pour la proportion correspond à la queue gauche, l’hypothèse nulle est rejetée si la statistique est inférieure à la valeur critique -Z _α .

$\begin{array}{l}H_1: p\neq p_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } |Z|>Z_{\alpha/2} \text{ se rechaza } H_0\\[3ex]H_1: p> p_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } Z>Z_{\alpha} \text{ se rechaza } H_0\\[3ex]H_1: p< p_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } Z<-Z_{\alpha} \text{ se rechaza } H_0\end{array}$

N’oubliez pas que les valeurs critiques peuvent être facilement obtenues à partir du tableau de distribution normale.

➤ Voir : Tableau de la distribution normale

Exemple de test d’hypothèse pour la proportion

Une fois que nous aurons vu la définition du test d’hypothèse pour la proportion et quelle est sa formule, nous allons résoudre un exemple pour mieux comprendre le concept.

Selon son fabricant, un médicament contre une maladie spécifique est efficace à 70 %. En laboratoire, on teste l’efficacité de ce médicament puisque les chercheurs estiment que la proportion est différente. Pour cela, le médicament est testé sur un échantillon de 1 000 malades et 641 personnes sont guéries. Effectuez un test d’hypothèse sur la proportion de population avec un niveau de signification de 5% pour rejeter ou non l’hypothèse des chercheurs.

Dans ce cas, l’hypothèse nulle et l’hypothèse alternative du test d’hypothèse pour la proportion de population sont les suivantes :

$\begin{cases}H_0: p=0,70\\[2ex] H_1:p\neq 0,70 \end{cases}$

La proportion de personnes dans l’échantillon qui ont été guéries grâce au médicament est :

$\widehat{p}=\cfrac{641}{1000}=0,641$

Nous calculons la statistique du test d’hypothèse pour la proportion en appliquant la formule vue ci-dessus :

$\begin{aligned} \displaystyle Z&=\frac{\widehat{p}-p}{\displaystyle\sqrt{\frac{p(1-p)}{n}}}\\[2ex]Z&=\frac{0,641-0,70}{\displaystyle\sqrt{\frac{0,70\cdot (1-0,70)}{1000}}} \\[2ex] Z&=-4,07\end{aligned}}$

D’un autre côté, puisque le niveau de signification est de 0,05 et qu’il s’agit d’un test d’hypothèse bilatéral, la valeur critique du test est de 1,96.

$Z_{0,025}=1,96$

➤ Voir : Niveau de signification 0,05

En conclusion, la valeur absolue de la statistique du test est supérieure à la valeur critique, nous rejetons donc l’hypothèse nulle et acceptons l’hypothèse alternative.

$|-4,07|=4,07>1,96 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Se rechaza } H_0$

➤ Voir : Test d’hypothèse pour la moyenne

Test d’hypothèse pour deux proportions d’échantillon

Les tests d’hypothèse pour les proportions de deux échantillons sont utilisés pour rejeter ou accepter l’hypothèse nulle selon laquelle les proportions de deux populations différentes sont égales.

Ainsi, l’hypothèse nulle d’un test d’hypothèse pour des proportions à deux échantillons est toujours la suivante :

$H_0: p_1=p_2$

Alors que l’hypothèse alternative peut être l’une des trois options suivantes :

*** QuickLaTeX cannot compile formula:
\begin{array}{l}H_1:p_1\neq p_2\\[2ex]H_1:p_1>p_2\\[2ex]H_1:p_1 Le ratio combiné des deux échantillons est calculé comme suit :[latex]p=\cfrac{x_1+x_2}{n_1+n_2}

*** Error message:
Missing $ inserted.
leading text: \begin{array}{l}
Please use \mathaccent for accents in math mode.
leading text: ...H_1:p_1>p_2\\[2ex]H_1:p_1 Le ratio combiné
Please use \mathaccent for accents in math mode.
leading text: ...\[2ex]H_1:p_1 Le ratio combiné des deux é
Please use \mathaccent for accents in math mode.
leading text: ...ombiné des deux échantillons est calculé
\begin{array} on input line 8 ended by \end{document}.
leading text: \end{document}
Improper \prevdepth.
leading text: \end{document}
Missing $ inserted.
leading text: \end{document}
Missing } inserted.
leading text: \end{document}
Missing \cr inserted.
leading text: \end{document}
Missing $ inserted.
leading text: \end{document}
You can't use `\end' in internal vertical mode.

Et la formule pour calculer la statistique du test d’hypothèse pour les proportions de deux échantillons est la suivante :

$\displaystyle Z=\frac{\displaystyle \frac{x_1}{n_1}-\frac{x_2}{n_2}}{\displaystyle \sqrt{p(1-p)\left(\frac{1}{n_1}+\frac{1}{n_2}\right)}}$

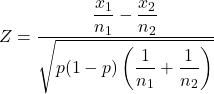
Où:

$Z$ est la statistique du test d’hypothèse pour les proportions de deux échantillons.
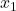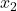$x_1$ est le nombre de résultats dans l’échantillon 1.
$x_2$ est le nombre de résultats dans l’échantillon 2.
$n_1$ est la taille de l’échantillon 1.
$n_2$ est la taille de l’échantillon 2.
$p$ est la proportion combinée des deux échantillons.

Test d’hypothèse pour k proportions d’échantillon

Dans un test d’hypothèse sur les proportions de k échantillons, le but est de déterminer si toutes les proportions des différentes populations sont égales ou, au contraire, s’il existe des proportions différentes. Par conséquent, l’hypothèse nulle et l’hypothèse alternative dans ce cas sont :

$\begin{cases}H_0: \text{Todas las proporciones son iguales}\\[2ex] H_1: \text{No todas las proporciones son iguales} \end{cases}$

Dans ce cas, la proportion combinée de tous les échantillons est calculée comme suit :

$p=\cfrac{\displaystyle\sum_{i=1}^k x_i}{\displaystyle\sum_{i=1}^k n_i}=\cfrac{x_1+x_2+\dots+x_k}{n_1+n_2+\dots+n_k}$

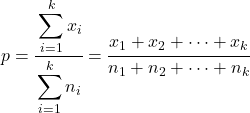
La formule permettant de trouver la statistique du test d’hypothèse pour les proportions de k échantillons est la suivante :

$\displaystyle \chi^2 =\sum_{i=1}^k \frac{(x_i-e_i)^2}{e_i}$

$\displaystyle\chi^2 = \frac{(x_1-e_1)^2}{e_1} +\frac{(x_2-e_2)^2}{e_2} +\dots+\frac{(x_k-e_k)^2}{e_k}$

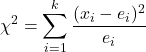
Où:

$\chi^2$ est la statistique du test d’hypothèse pour les proportions de k échantillons. Dans ce cas, la statistique suit une distribution du chi carré.
$x_i$ est le nombre de résultats dans l’échantillon i.
$n_i$ est la taille de l’échantillon i.
$p$ est la proportion combinée de tous les échantillons.
$e_i$ est le nombre de hits attendus de l’échantillon i. Il est calculé en multipliant la proportion combinée $p$ par la taille de l’échantillon $n_i$ .

à propos de l'auteur

Pr Amélia Rodriguez

En mettant l'accent sur l'apprentissage interactif et les applications pratiques, la professeure Amélia Rodriguez propose des tutoriels complets et des exemples concrets pour rendre les concepts de probabilité accessibles et pertinents pour la vie de ses étudiants. Lire plus