Qu’est-ce qu’un test multinomial ? (Définition & #038; Exemple)

Un test multinomial est utilisé pour déterminer si une variable catégorielle suit une distribution hypothétique.

Ce test utilise les hypothèses nulles et alternatives suivantes :

H ₀ : Une variable catégorielle suit une distribution hypothétique.

H _A : Une variable catégorielle ne suit pas la distribution hypothétique.

Si la valeur p du test est inférieure à un certain niveau de signification (par exemple α = 0,05), nous pouvons alors rejeter l’hypothèse nulle et conclure que la variable ne suit pas la distribution hypothétique.

Ce test est utilisé lorsqu’une variable peut prendre k résultats différents. Un exemple classique de test multinomial est celui où nous souhaitons déterminer si certains dés sont justes. Lorsque l’on lance un dé, la probabilité qu’il tombe sur chaque chiffre (1 à 6) est de 1/6.

Pour tester si un dé est équitable, nous pourrions le lancer un certain nombre de fois et voir si le nombre de fois où il tombe sur différents nombres est significativement différent de ce à quoi nous nous attendrions.

Les exemples suivants montrent comment effectuer un test multinomial à l’aide du langage de programmation statistique R.

Exemple 1 : dés équitables

Supposons que nous souhaitons déterminer si un dé est juste. Pour tester cela, nous le lançons 30 fois et enregistrons la fréquence de chaque résultat. Le tableau suivant montre les résultats :

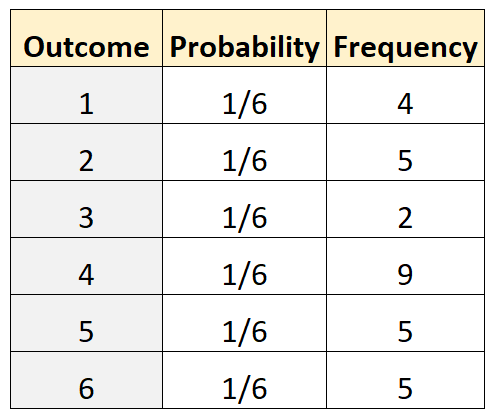
Le code suivant dans R peut être utilisé pour effectuer un test multinomial :

library(EMT)

#specify probability of each outcome
prob <- c(1/6, 1/6, 1/6, 1/6, 1/6, 1/6)

#specify frequency of each outcome from experiment
actual <- c(4, 5, 2, 9, 5, 5)

#perform multinomial test
multinomial.test(actual, prob)  

 Exact Multinomial Test, distance measure: p

    Events    pObs    p.value
    324632       0     0.4306

La valeur p du test est de 0,4306 . Puisque cette valeur p n’est pas inférieure à 0,05, nous ne rejetterons pas l’hypothèse nulle. Nous n’avons donc pas suffisamment de preuves pour affirmer que les dés sont injustes.

Exemple 2 : Ventes de produits

Supposons qu’un propriétaire de magasin émette l’hypothèse qu’un nombre égal de clients achèteront chacun des quatre produits différents. Pour tester cela, il enregistre le nombre de clients qui achètent chaque produit au cours d’une semaine donnée. Le tableau suivant montre les résultats :

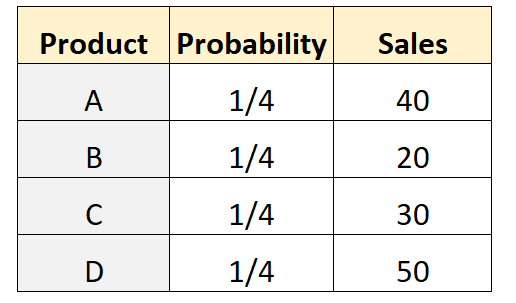
Le code suivant dans R peut être utilisé pour effectuer un test multinomial sur cet ensemble de données :

library(EMT)

#specify probability of each outcome
prob <- c(1/4, 1/4, 1/4, 1/4)

#specify frequency of each outcome from experiment
actual <- c(40, 20, 30, 50)

#perform multinomial test
multinomial.test(actual, prob)  

 Exact Multinomial Test, distance measure: p

    Events    pObs    p.value
    477191       0     0.00226

La valeur p du test est de 0,00226 . Puisque cette valeur p est inférieure à 0,05, nous rejetterons l’hypothèse nulle. Ainsi, nous disposons de preuves suffisantes pour affirmer que les ventes ne sont pas égales pour chaque produit.

Exemple 3 : Billes dans un sac

Tom affirme que la probabilité de choisir une bille rouge, verte ou violette dans un sac est respectivement de 0,2, 0,5 et 0,3. Pour tester cela, son ami Mike fouille dans le sac et en sort une bille (avec remplacement) 100 fois différentes. Le tableau suivant montre les résultats :

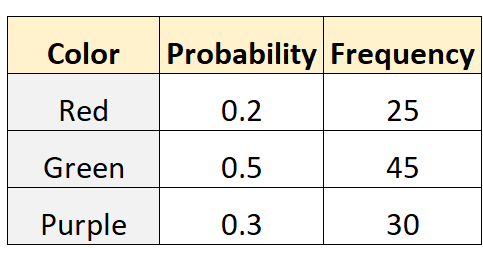
Le code suivant dans R peut être utilisé pour effectuer un test multinomial sur cet ensemble de données :

library(EMT)

#specify probability of each outcome
prob <- c(.2, .5, .3)

#specify frequency of each outcome from experiment
actual <- c(40, 20, 30, 50)

#perform multinomial test
multinomial.test(actual, prob)  

 Exact Multinomial Test, distance measure: p

    Events    pObs    p.value
      5151  0.0037     0.3999

La valeur p du test est de 0,3999 . Puisque cette valeur p n’est pas inférieure à 0,05, nous ne parviendrons pas à rejeter l’hypothèse nulle. Nous n’avons donc pas suffisamment de preuves pour affirmer que la répartition des billes dans le sac est différente de celle précisée par Tom.

Ressources additionnelles

Une introduction à la distribution multinomiale
Calculateur de distribution multinomiale