Comment tester la signification d’une pente de régression

Supposons que nous disposions de l’ensemble de données suivant qui montre la superficie en pieds carrés et le prix de 12 maisons différentes :

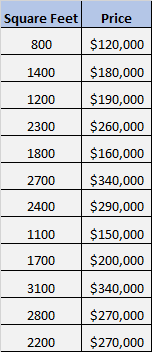
Nous voulons savoir s’il existe une relation significative entre les pieds carrés et le prix.

Pour avoir une idée de ce à quoi ressemblent les données, nous créons d’abord un nuage de points avec les pieds carrés sur l’axe des x et le prix sur l’axe des y :

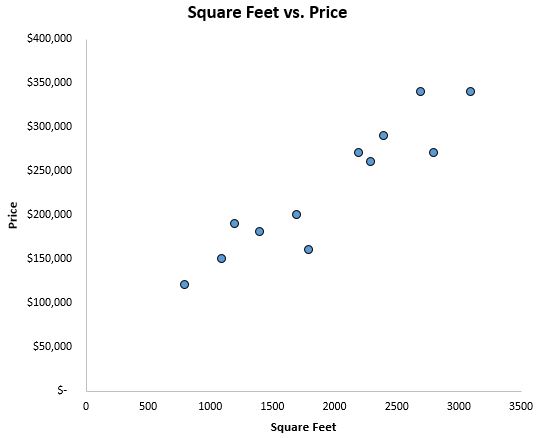
Nous pouvons clairement voir qu’il existe une corrélation positive entre les pieds carrés et le prix. À mesure que la superficie en pieds carrés augmente, le prix de la maison a également tendance à augmenter.

Cependant, pour savoir s’il existe une relation statistiquement significative entre les pieds carrés et le prix, nous devons exécuter une simple régression linéaire.

Nous effectuons donc une régression linéaire simple en utilisant les pieds carrés comme prédicteur et le prix comme réponse et obtenons le résultat suivant :

Que vous exécutiez une simple régression linéaire dans Excel, SPSS, R ou tout autre logiciel, vous obtiendrez un résultat similaire à celui présenté ci-dessus.

Rappelez-vous qu’une simple régression linéaire produira la droite de meilleur ajustement, qui est l’équation de la droite qui « correspond » le mieux aux données de notre nuage de points. Cette ligne de meilleur ajustement est définie comme :

ŷ = b ₀ + b ₁ x

où ŷ est la valeur prédite de la variable de réponse, b ₀ est l’ordonnée à l’origine, b ₁ est le coefficient de régression et x est la valeur de la variable prédictive.

La valeur de b ₀ est donnée par le coefficient de l’origine, qui est 47588,70.

La valeur de b ₁ est donnée par le coefficient de la variable prédictive Square Feet , qui est 93,57.

Ainsi, la droite la mieux ajustée dans cet exemple est ŷ = 47588,70+ 93,57x

Voici comment interpréter cette ligne de meilleur ajustement :

• b ₀ : Lorsque la valeur des pieds carrés est nulle, la valeur moyenne attendue du prix est de 47 588,70 $. (Dans ce cas, cela n’a pas vraiment de sens d’interpréter l’interception, puisqu’une maison ne peut jamais avoir zéro pied carré)
• b ₁ : Pour chaque pied carré supplémentaire, l’augmentation moyenne attendue du prix est de 93,57 $.

Ainsi, nous savons maintenant que pour chaque pied carré supplémentaire, l’augmentation moyenne attendue du prix est de 93,57 $.

Pour savoir si cette augmentation est statistiquement significative, nous devons effectuer un test d’hypothèse pour B ₁ ou construire un intervalle de confiance pour B ₁ .

Remarque : Un test d’hypothèse et un intervalle de confiance donneront toujours les mêmes résultats.

Construction d’un intervalle de confiance pour une pente de régression

Pour construire un intervalle de confiance pour une pente de régression, nous utilisons la formule suivante :

Intervalle de confiance = b ₁ +/- (t _{1-∝/2, n-2} ) * (erreur type de b ₁ )

où:

• b ₁ est le coefficient de pente donné dans le résultat de la régression
• (t _{1-∝/2, n-2} ) est la valeur critique t pour le niveau de confiance 1-∝ avec n-2 degrés de liberté où n est le nombre total d’observations dans notre ensemble de données
• (erreur type de b ₁ ) est l’erreur type de b ₁ donnée dans le résultat de la régression

Pour notre exemple, voici comment construire un intervalle de confiance à 95 % pour B ₁ :

• b ₁ est 93,57 à partir de la sortie de régression.
• Puisque nous utilisons un intervalle de confiance à 95 %, ∝ = 0,05 et n-2 = 12-2 = 10, donc t _{0,975, 10} est 2,228 selon le tableau de distribution t
• (l’erreur standard de b ₁ ) est de 11,45 à partir de la sortie de régression

Ainsi, notre intervalle de confiance à 95 % pour B ₁ est :

93,57 +/- (2,228) * (11,45) = (68,06 , 119,08)

Cela signifie que nous sommes convaincus à 95 % que la véritable augmentation moyenne du prix pour chaque pied carré supplémentaire se situe entre 68,06 $ et 119,08 $.

Notez que 0 $ n’est pas dans cet intervalle, donc la relation entre les pieds carrés et le prix est statistiquement significative au niveau de confiance de 95 %.

Réalisation d’un test d’hypothèse pour une pente de régression

Pour effectuer un test d’hypothèse pour une pente de régression, nous suivons les cinq étapes standard pour tout test d’hypothèse :

Étape 1. Énoncez les hypothèses.

L’hypothèse nulle (H0) : B ₁ = 0

L’hypothèse alternative : (Ha) : B ₁ ≠ 0

Étape 2. Déterminez un niveau de signification à utiliser.

Puisque nous avons construit un intervalle de confiance de 95 % dans l’exemple précédent, nous utiliserons ici l’approche équivalente et choisirons d’utiliser un niveau de signification de 0,05.

Étape 3. Recherchez la statistique du test et la valeur p correspondante.

Dans ce cas, la statistique de test est t = coefficient de b ₁ / erreur type de b ₁ avec n-2 degrés de liberté. Nous pouvons trouver ces valeurs à partir du résultat de la régression :

Ainsi, la statistique de test t = 92,89 / 13,88 = 6,69.

En utilisant le calculateur de score T vers valeur P avec un score de 6,69 avec 10 degrés de liberté et un test bilatéral, la valeur p = 0,000 .

Étape 4. Rejetez ou ne rejetez pas l’hypothèse nulle.

Étant donné que la valeur p est inférieure à notre niveau de signification de 0,05, nous rejetons l’hypothèse nulle.

Étape 5. Interprétez les résultats.

Puisque nous avons rejeté l’hypothèse nulle, nous disposons de suffisamment de preuves pour affirmer que la véritable augmentation moyenne du prix pour chaque pied carré supplémentaire n’est pas nulle.