Comment effectuer un test t pour échantillons appariés dans SAS

Un test t pour échantillons appariés est utilisé pour comparer les moyennes de deux échantillons lorsque chaque observation dans un échantillon peut être associée à une observation dans l’autre échantillon.

Ce didacticiel explique comment effectuer un test t pour échantillons appariés dans SAS.

Exemple : test t pour échantillons appariés dans SAS

Supposons qu’un professeur souhaite déterminer si un certain programme d’études affecte les résultats des tests. Pour tester cela, il sélectionne au hasard 15 étudiants pour passer un pré-test. Ensuite, il fait utiliser à chaque élève le programme d’études pendant un mois puis un post-test de difficulté similaire.

Les résultats des tests de chacun des 15 étudiants sont indiqués ci-dessous :

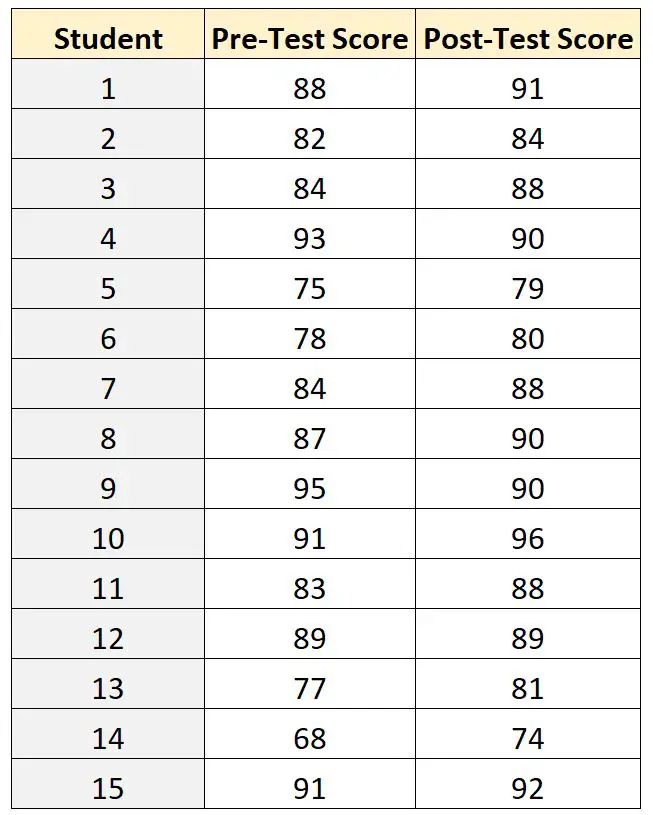
Pour comparer la différence entre les scores moyens au pré-test et au post-test, le professeur peut utiliser un test t pour échantillons appariés car pour chaque étudiant, son score pré-test peut être associé à son score post-test.

Suivez les étapes suivantes pour effectuer ce test t pour échantillons appariés dans SAS :

Étape 1 : Créer les données

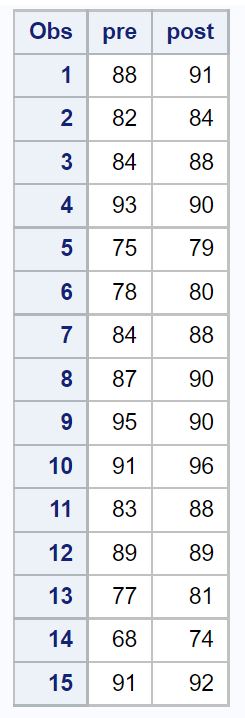
Tout d’abord, utilisons le code suivant pour créer l’ensemble de données dans SAS :

/*create dataset*/
data test_scores;
    input pre post;
    datalines;
88 91
82 84
84 88
93 90
75 79
78 80
84 88
87 90
95 90
91 96
83 88
89 89
77 81
68 74
91 92
;
run;

/*view dataset*/
proc print data=test_scores;

Étape 2 : Effectuer le test t pour échantillons appariés

Ensuite, nous pouvons utiliser proc tttest pour effectuer le test t pour échantillons appariés :

/*perform paired samples t-test*/
proc ttest data=test_scores alpha=.05;
    paired pre*post;
run;

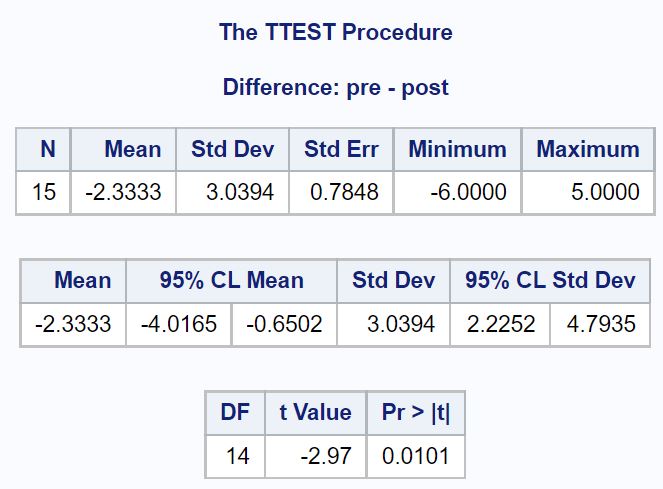
À partir du résultat, nous pouvons voir ce qui suit :

• Différence moyenne entre le score pré-test et post-test : -2,3333
• Intervalle de confiance à 95 % pour la différence moyenne : [-4,0165, -0,6502]

Nous pouvons également voir la statistique du test t et la valeur p bilatérale correspondante :

• statistique du test t : -2,97
• Valeur p : 0,0101

Dans cet exemple, le test t pour échantillons appariés utilise les hypothèses nulles et alternatives suivantes :

• H ₀ : Les scores moyens pré-test et post-test sont égaux
• H _A : Les scores moyens pré-test et post-test ne sont pas égaux

Puisque la valeur p ( 0,0101 ) est inférieure à 0,05, nous rejetons l’hypothèse nulle.

Cela signifie que nous disposons de suffisamment de preuves pour affirmer que le véritable score moyen au test est différent pour les étudiants avant et après leur participation au programme d’études.

Ressources additionnelles

Les didacticiels suivants expliquent comment effectuer d’autres tests statistiques courants dans SAS :

Comment effectuer un test t sur un échantillon dans SAS
Comment effectuer un test t à deux échantillons dans SAS
Comment effectuer un test de classement signé Wilcoxon dans SAS