Test t de Student

Par Pr Amélia Rodriguez août 3, 2023 Statistiques 0 commentaire

Cet article explique ce qu’est le test t de Student et à quoi il sert en statistiques. Ainsi, vous découvrirez comment est réalisé le test t de Student, quels sont les différents types de tests t de Student, et la formule pour chacun.

Qu’est-ce que le test t de Student ?

Le test t de Student , également appelé test T ou simplement test t , est un test statistique dans lequel la statistique du test suit la distribution t de Student . Par conséquent, en statistique, le test t de Student est utilisé pour rejeter ou accepter l’hypothèse nulle d’un test d’hypothèse.

Plus précisément, le test t de Student est utilisé dans les tests d’hypothèses dans lesquels la population étudiée suit une distribution normale, mais la taille de l’échantillon est trop petite pour connaître la variance de la population.

En bref, le test t de Student est utilisé pour rejeter ou accepter l’hypothèse d’étude de certains tests d’hypothèse. Par exemple, le test t de Student est utilisé pour tester des hypothèses pour un échantillon, pour des échantillons indépendants ou pour des échantillons liés. Nous verrons ensuite comment le test t de Student est calculé dans chaque cas.

Types de tests t de Student

Il existe trois types de tests t de Student :

Test t de Student pour un échantillon – est utilisé pour tester l’hypothèse sur la valeur de la moyenne d’un échantillon.
Test t de Student pour deux échantillons indépendants : il permet de tester l’hypothèse sur la différence entre les moyennes de deux échantillons indépendants.
Le test t de Student pour deux échantillons appariés (ou échantillons apparentés) – est utilisé pour étudier l’hypothèse sur la moyenne d’un échantillon testé deux fois.

Un échantillon du test t de Student

Les tests d’hypothèse pour la moyenne d’un échantillon sont ceux dans lesquels l’hypothèse nulle et l’hypothèse alternative du test indiquent quelque chose sur la valeur de la moyenne d’une population.

La formule du test t de Student pour un échantillon est la suivante :

$\displaystyle t=\frac{\overline{x}-\mu}{\displaystyle \frac{s}{\sqrt{n}}}$

Où:

$t$ est la statistique du test d’hypothèse pour la moyenne, qui est définie par la distribution t de Student.
$\overline{x}$ est la moyenne de l’échantillon.
$\mu$ est la valeur de la moyenne proposée dans le test d’hypothèse.
$s$ est l’écart type de l’échantillon.
$n$ est la taille de l’échantillon.

Une fois la valeur du test t de Student calculée, le résultat du test statistique avec la valeur critique doit être interprété pour rejeter ou non l’hypothèse nulle :

Si le test d’hypothèse pour la moyenne est bilatéral, l’hypothèse nulle est rejetée si la valeur absolue du test t de Student est supérieure à la valeur critique t _α/2|n-1 .
Si le test d’hypothèse pour la moyenne correspond à la queue droite, l’hypothèse nulle est rejetée si la valeur du test t de Student est supérieure à la valeur critique t _α|n-1 .
Si le test d’hypothèse pour la moyenne correspond à la queue gauche, l’hypothèse nulle est rejetée si la valeur du test t de Student est inférieure à la valeur critique -t _α|n-1 .

$\begin{array}{l}H_1: \mu\neq \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } |t|>t_{\alpha/2|n-1} \text{ se rechaza } H_0\\[3ex]H_1: \mu> \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } t>t_{\alpha|n-1} \text{ se rechaza } H_0\\[3ex]H_1: \mu< \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } t<-t_{\alpha|n-1} \text{ se rechaza } H_0\end{array}$

Notez que les valeurs critiques du test sont obtenues à partir du tableau de distribution t de Student.

➤ Voir : Exemple concret du test d’hypothèse pour la moyenne

Test t de Student pour échantillons indépendants

Le test t de Student pour échantillons indépendants est utilisé pour rejeter ou accepter l’hypothèse d’une relation entre les moyennes de deux populations, par exemple, que les moyennes de deux populations sont différentes ou que la moyenne de la population A est supérieure à la moyenne de. la population B.

Cependant, dans ce cas, la formule du test t de Student varie selon que l’on peut supposer que les variances de la population sont égales ou non. Nous verrons donc ensuite les deux cas possibles.

Écarts inconnus et égaux

La formule permettant de calculer le test t de Student pour des échantillons indépendants lorsque les variances de la population sont inconnues mais supposées égales est la suivante :

$\displaystyle t=\frac{\displaystyle (\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\displaystyle s_p\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}}$

Où:

$t$ est la statistique de test d’hypothèse pour la différence des moyennes avec des variances inconnues, qui suit une distribution t de Student avec n ₁ + n ₂ -2 degrés de liberté.
$\mu_1$ est la moyenne de la population 1.
$\mu_2$ est la moyenne de la population 2.
$\overline{x_1}$ est la moyenne de l’échantillon 1.
$\overline{x_2}$ est la moyenne de l’échantillon 2.
$s_p$ est l’écart type regroupé.
$n_1$ est la taille de l’échantillon 1.
$n_2$ est la taille de l’échantillon 2.

L’écart type combiné des deux échantillons est calculé à l’aide de la formule suivante :

$\displaystyle s_p=\sqrt{\frac{(n_1-1)s_1^2+(n_2-1)s_2^2}{n_1+n_2-2}}$

Variations inconnues et différentes

Lorsque les variances des populations sont inconnues et, de plus, supposées différentes, la formule pour calculer le test t de Student pour des échantillons indépendants est la suivante :

$\displaystyle t=\frac{\displaystyle (\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\displaystyle \sqrt{\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2}}}$

Où:

$t$ est la statistique de test d’hypothèse pour la différence des moyennes avec des variances inconnues, qui suit une distribution t de Student.
$\mu_1$ est la moyenne de la population 1.
$\mu_2$ est la moyenne de la population 2.
$\overline{x_1}$ est la moyenne de l’échantillon 1.
$\overline{x_2}$ est la moyenne de l’échantillon 2.
$\sigma_1$ est l’écart type de la population 1.
$\sigma_2$ est l’écart type de la population 2.
$n_1$ est la taille de l’échantillon 1.
$n_2$ est la taille de l’échantillon 2.

Cependant, dans ce cas, les degrés de liberté de la distribution t de Student sont calculés à l’aide de la formule suivante :

$\displaystyle GL=\frac{\displaystyle\left(\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2}\right)^2}{\displaystyle\frac{\displaystyle\frac{s_1^2}{n_1}}{n_1-1}+\frac{\displaystyle\frac{s_2^2}{n_2}}{n_2-1}}$

➤ Voir : Exemple concret du test d’hypothèse pour la différence de moyennes

Test t de Student pour les échantillons appariés ou apparentés

Ce test est utilisé lorsque deux échantillons étudiés sont liés entre eux, de sorte qu’il s’agit en réalité d’un seul échantillon d’individus qui a été analysé deux fois (à chaque fois dans des conditions différentes).

Par exemple, vous pouvez analyser les notes obtenues par les élèves dans un cours de mathématiques et de statistiques pour voir s’il existe une différence significative entre les moyennes des deux matières. Dans ce cas, la note en mathématiques de chaque élève est liée à la note en statistiques de ce même élève.

La formule du test t de Student pour les échantillons appariés ou apparentés est la suivante :

$\displaystyle t=\frac{\overline{x_D}-\mu_D}{\displaystyle \frac{s_D}{\sqrt{n}}}$

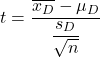
Où:

$t$ est la statistique de test d’hypothèse pour les moyennes appariées, qui est définie par la distribution t de Student.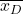
$\overline{x_D}$ est la moyenne de l’échantillon formé par la différence des données.
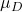$\mu_D$ est la valeur de la moyenne proposée dans le test d’hypothèse.
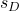$s_D$ est l’écart type de l’échantillon formé par la différence des données.
$n$ est la taille de l’échantillon.

Hypothèses du test t de Student

Afin d’effectuer le test t de Student, les conditions suivantes doivent être remplies :

Continuité – Les exemples de données sont continus.
Caractère aléatoire : les échantillons de données ont été sélectionnés de manière aléatoire.
Homogénéité : La variance de l’échantillon de données est homogène.
Normalité – La distribution qui définit l’échantillon de données est approximativement normale.

Comment faire un test t de Student

Enfin, en résumé, les étapes à suivre pour réaliser un test t de Student sont détaillées.

Définir les hypothèses nulles et alternatives du test d’hypothèse.
Établir le niveau de signification (α) du test d’hypothèse.
Vérifiez que les hypothèses du test t de Student sont remplies.
Appliquez la formule du test t de Student correspondante et calculez la statistique du test.
Interprétez le résultat du test t de Student en le comparant à la valeur critique du test.

à propos de l'auteur

Pr Amélia Rodriguez

En mettant l'accent sur l'apprentissage interactif et les applications pratiques, la professeure Amélia Rodriguez propose des tutoriels complets et des exemples concrets pour rendre les concepts de probabilité accessibles et pertinents pour la vie de ses étudiants. Lire plus