Comment effectuer un test t avec des tailles d’échantillon inégales

Une question que les étudiants se posent souvent en matière de statistiques est la suivante :

Est-il possible d’effectuer un test t lorsque les tailles d’échantillon de chaque groupe ne sont pas égales ?

La réponse courte :

Oui, vous pouvez effectuer un test t lorsque les tailles d’échantillon ne sont pas égales. Des tailles d’échantillon égales ne font pas partie des hypothèses formulées dans un test t.

Les vrais problèmes surviennent lorsque les deux échantillons n’ont pas des variances égales, ce qui est l’une des hypothèses formulées dans un test t.

Lorsque cela se produit, il est recommandé d’utiliser plutôt le test t de Welch , qui ne fait pas l’hypothèse de variances égales.

Les exemples suivants montrent comment effectuer des tests T avec des tailles d’échantillon inégales lorsque les variances sont égales et lorsqu’elles ne le sont pas.

Exemple 1 : Tailles d’échantillon inégales et variances égales

Supposons que nous administrions deux programmes conçus pour aider les étudiants à obtenir de meilleurs résultats à certains examens.

Les résultats sont les suivants:

Programme 1 :

• n (taille de l’échantillon) : 500
• x (moyenne de l’échantillon) : 80
• s (écart type de l’échantillon) : 5

Programme 2 :

• n (taille de l’échantillon) : 20
• x (moyenne de l’échantillon) : 85
• s (écart type de l’échantillon) : 5

Le code suivant montre comment créer un boxplot dans R pour visualiser la distribution des résultats des examens pour chaque programme :

#make this example reproducible
set.seed(1)

#create vectors to hold exam scores
program1 <- rnorm(500, mean=80, sd=5)
program2 <- rnorm(20, mean=85, sd=5)

#create boxplots to visualize distribution of exam scores
boxplot(program1, program2, names=c("Program 1","Program 2"))

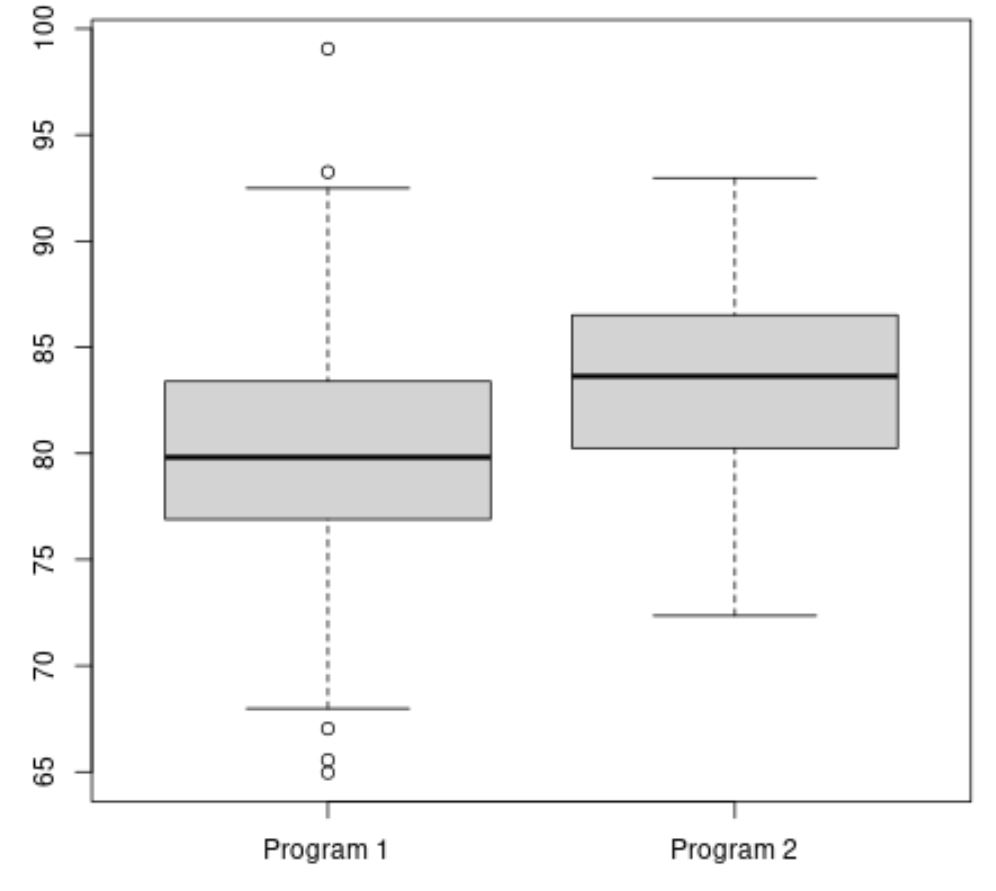
La note moyenne aux examens du programme 2 semble être plus élevée, mais la variance des notes aux examens entre les deux programmes est à peu près égale.

Le code suivant montre comment effectuer un test t pour échantillons indépendants avec un test t de Welch :

#perform independent samples t-test
t.test(program1, program2, var.equal=TRUE)

	Two Sample t-test

data:  program1 and program2
t = -3.3348, df = 518, p-value = 0.0009148
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -6.111504 -1.580245
sample estimates:
mean of x mean of y 
 80.11322  83.95910

#perform Welch's two sample t-test
t.test(program1, program2, var.equal=FALSE)

	Welch Two Sample t-test

data:  program1 and program2
t = -3.3735, df = 20.589, p-value = 0.00293
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -6.219551 -1.472199
sample estimates:
mean of x mean of y 
 80.11322  83.95910 

Le test t pour échantillons indépendants renvoie une valeur p de 0,0009 et le test t de Welch renvoie une valeur p de 0,0029 .

Étant donné que la valeur p de chaque test est inférieure à 0,05, nous rejetterions l’hypothèse nulle dans chaque test et conclurions qu’il existe une différence statistiquement significative dans les résultats moyens aux examens entre les deux programmes.

Même si les tailles d’échantillon sont inégales, le test t pour échantillons indépendants et le test t de Welch renvoient tous deux des résultats similaires puisque les deux échantillons présentaient des variances égales.

Exemple 2 : Tailles d’échantillon inégales et variances inégales

Supposons que nous administrions deux programmes conçus pour aider les étudiants à obtenir de meilleurs résultats à certains examens.

Les résultats sont les suivants:

Programme 1 :

• n (taille de l’échantillon) : 500
• x (moyenne de l’échantillon) : 80
• s (écart type de l’échantillon) : 25

Programme 2 :

• n (taille de l’échantillon) : 20
• x (moyenne de l’échantillon) : 85
• s (écart type de l’échantillon) : 5

Le code suivant montre comment créer un boxplot dans R pour visualiser la distribution des résultats des examens pour chaque programme :

#make this example reproducible
set.seed(1)

#create vectors to hold exam scores
program1 <- rnorm(500, mean=80, sd=25)
program2 <- rnorm(20, mean=85, sd=5)

#create boxplots to visualize distribution of exam scores
boxplot(program1, program2, names=c("Program 1","Program 2"))

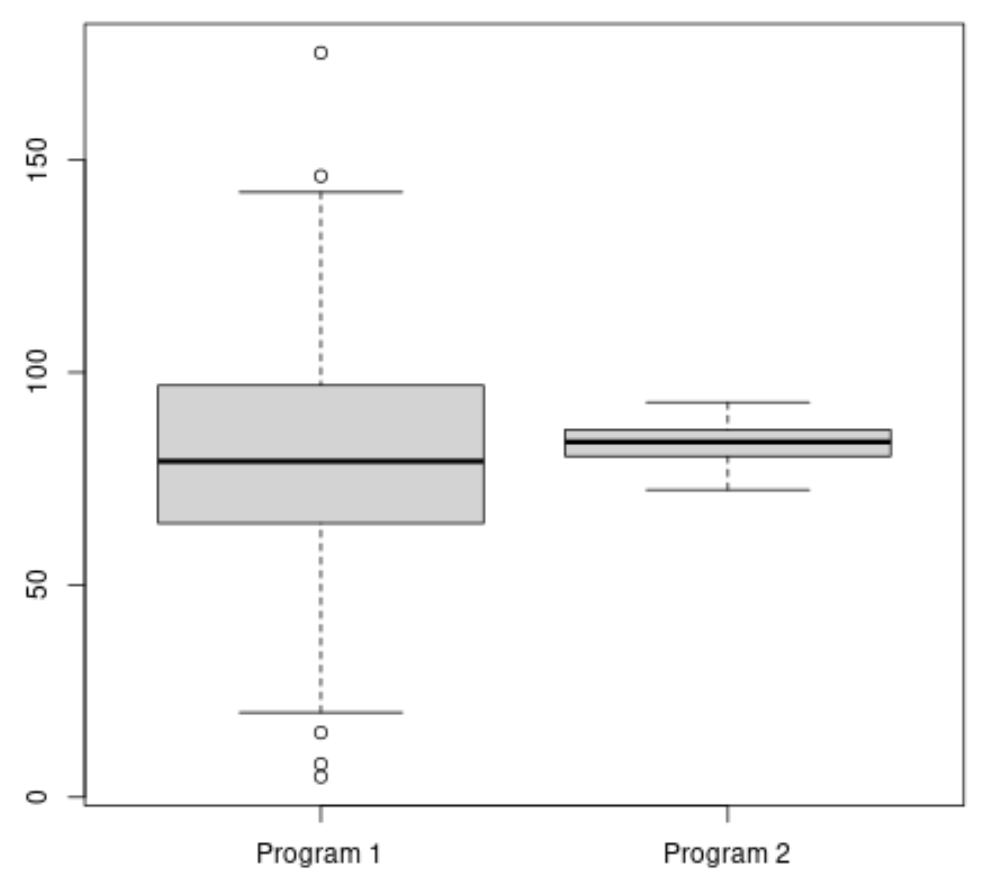
La note moyenne aux examens du programme 2 semble être plus élevée, mais la variance des notes aux examens du programme 1 est beaucoup plus élevée que celle du programme 2.

Le code suivant montre comment effectuer un test t pour échantillons indépendants avec un test t de Welch :

#perform independent samples t-test
t.test(program1, program2, var.equal=TRUE)

	Two Sample t-test

data:  program1 and program2
t = -0.5988, df = 518, p-value = 0.5496
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -14.52474   7.73875
sample estimates:
mean of x mean of y 
  80.5661   83.9591

#perform Welch's two sample t-test
t.test(program1, program2, var.equal=FALSE)

	Welch Two Sample t-test

data:  program1 and program2
t = -2.1338, df = 74.934, p-value = 0.03613
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -6.560690 -0.225296
sample estimates:
mean of x mean of y 
  80.5661   83.9591 

Le test t pour échantillons indépendants renvoie une valeur p de 0,5496 et le test t de Welch renvoie une valeur p de 0,0361 .

Le test t pour échantillons indépendants n’est pas capable de détecter une différence dans les résultats moyens aux examens, mais le test t de Welch est capable de détecter une différence statistiquement significative.

Étant donné que les deux échantillons présentaient des variances inégales, seul le test t de Welch a pu détecter la différence statistiquement significative dans les résultats moyens aux examens, car ce test ne fait pas l’hypothèse de variances égales entre les échantillons .

Ressources additionnelles

Les didacticiels suivants fournissent des informations supplémentaires sur les tests t :

Introduction au test t sur un échantillon
Introduction au test t à deux échantillons
Introduction au test t pour échantillons appariés