Comment appliquer Bayes’ Théorème dans Excel

Le théorème de Bayes énonce ce qui suit pour deux événements A et B :

P(UNE|B) = P(UNE)*P(B|UNE) / P(B)

où:

• P(A|B) : La probabilité que l’événement A, étant donné que l’événement B, se soit produit.
• P(B|A) : La probabilité que l’événement B, étant donné que l’événement A s’est produit, s’est produit.
• P(A) : La probabilité de l’événement A.
• P(B) : La probabilité de l’événement B.

Par exemple, supposons que la probabilité que le temps soit nuageux est de 40 %. Supposons également que la probabilité de pluie un jour donné soit de 20 % et que la probabilité de nuages un jour de pluie soit de 85 %.

S’il fait nuageux dehors un jour donné, quelle est la probabilité qu’il pleuve ce jour-là ?

Solution :

• P(nuageux) = 0,40
• P(pluie) = 0,20
• P(nuageux | pluie) = 0,85

Ainsi, on peut calculer :

• P(pluie | nuageux) = P(pluie) * P(nuageux | pluie) / P(nuageux)
• P(pluie | nuageux) = 0,20 * 0,85 / 0,40
• P(pluie | nuageux) = 0,425

S’il fait nuageux dehors un jour donné, la probabilité qu’il pleuve ce jour-là est de 0,425 ou 42,5 % .

L’exemple suivant montre comment résoudre ce problème précis à l’aide du théorème de Bayes dans Excel.

Exemple : théorème de Bayes dans Excel

La formule suivante montre comment appliquer le théorème de Bayes dans Excel :

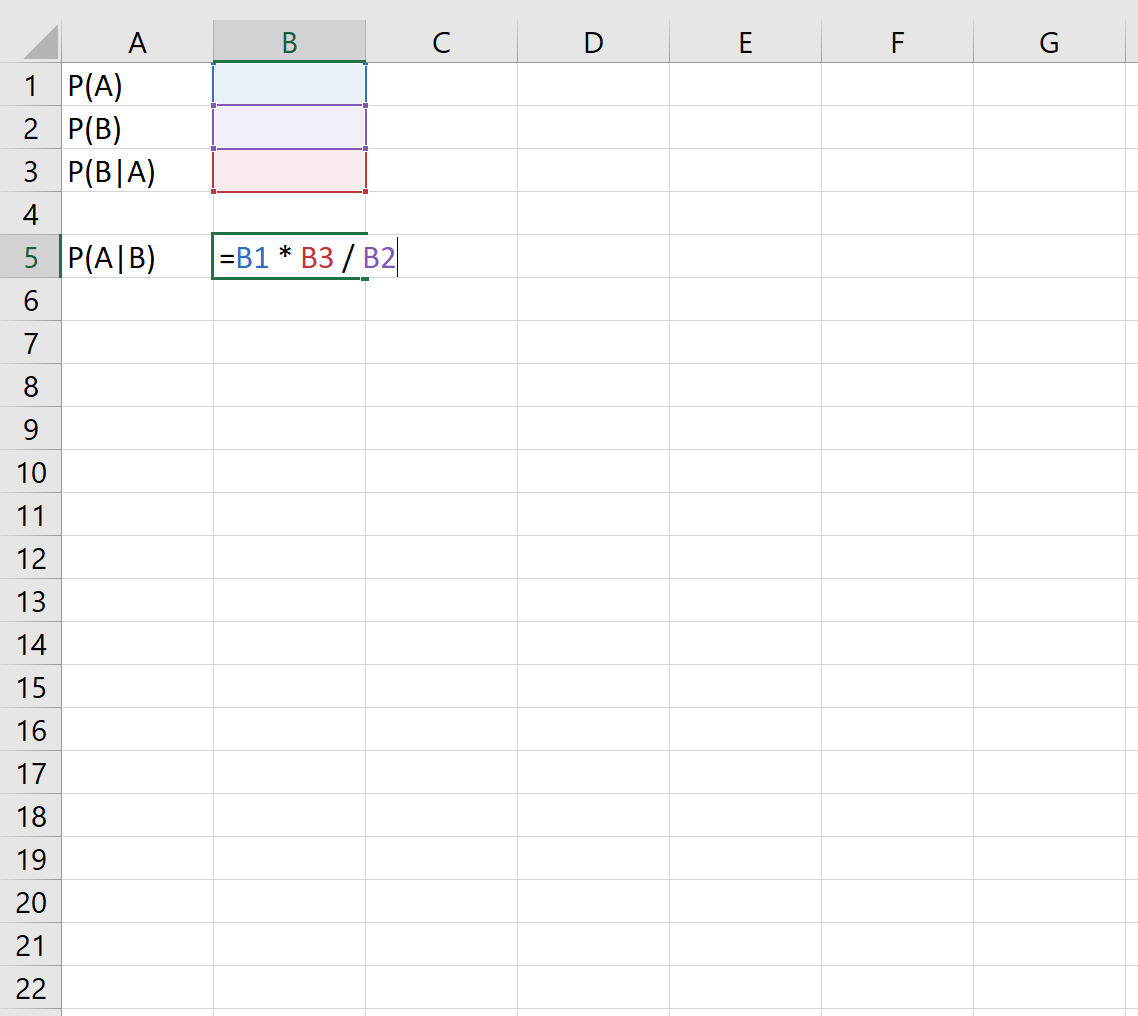
Par exemple, si nous connaissons les probabilités suivantes :

• P(nuageux) = 0,40
• P(pluie) = 0,20
• P(nuageux | pluie) = 0,85

Ensuite, nous pouvons simplement les brancher dans les cellules d’Excel :

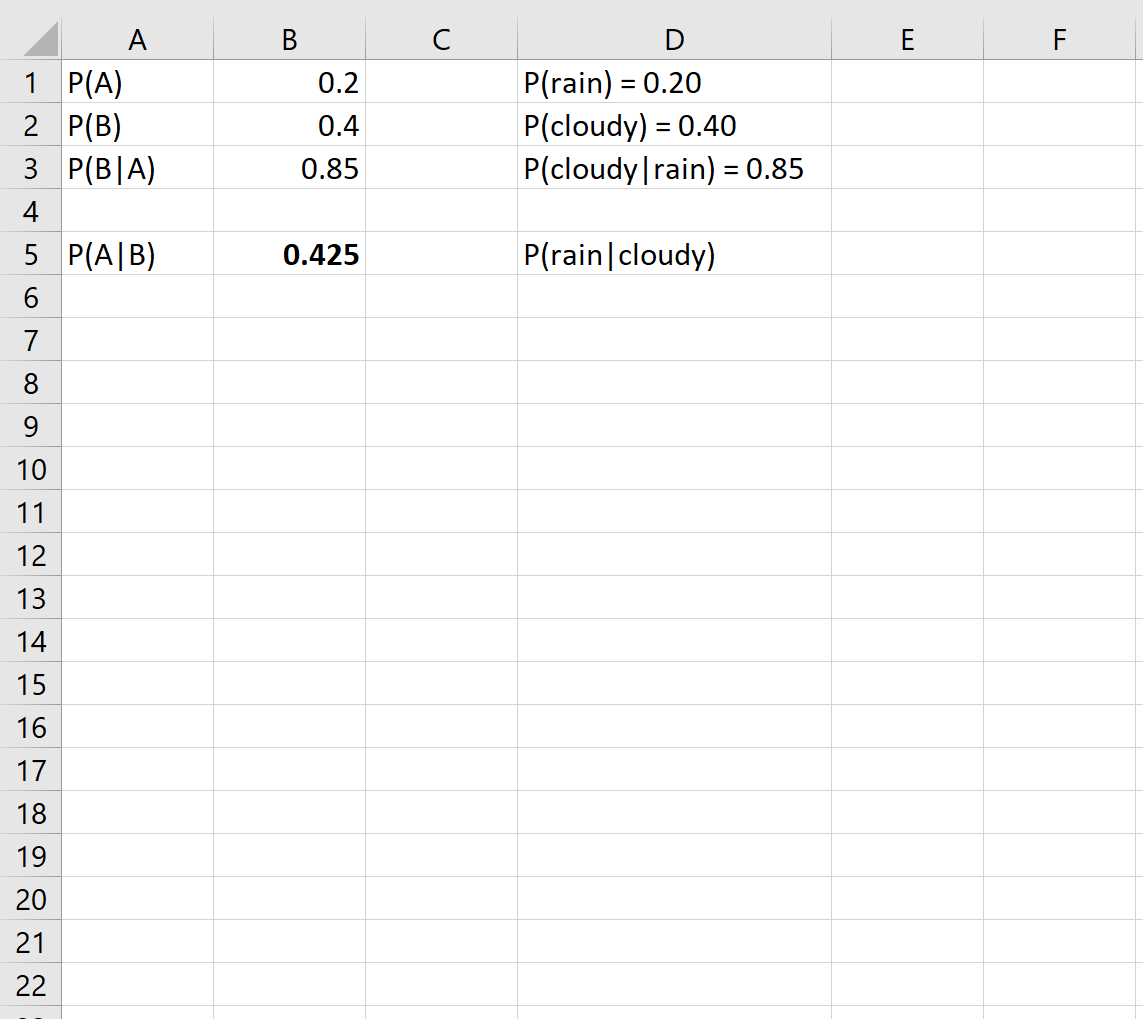
Cela nous indique que s’il fait nuageux dehors un jour donné, la probabilité qu’il pleuve ce jour-là est de 0,425 ou 42,5 % .

Ressources additionnelles

Comment calculer la probabilité conditionnelle dans Excel
Comment appliquer la règle empirique dans Excel
Comment appliquer le théorème central limite dans Excel