Théorème de Bayes

Par août 1, 2023 Probabilité 0 commentaire

Cet article explique ce qu’est le théorème de Bayes et à quoi il sert en probabilités et en statistiques. Ainsi, vous découvrirez quelle est la formule du théorème de Bayes, des exemples résolus du théorème de Bayes et quelles sont les applications de ce théorème.

Qu’est-ce que le théorème de Bayes ?

En théorie des probabilités, le théorème de Bayes est une loi utilisée pour calculer la probabilité d’un événement lorsque des informations a priori sur cet événement sont connues.

Plus précisément, le théorème de Bayes relie mathématiquement la probabilité d’un événement A étant donné l’événement B à la probabilité de B étant donné A.

Par exemple, si vous connaissez à l’avance la probabilité qu’une personne ait mal à la tête lorsqu’elle a la grippe, vous pouvez utiliser le théorème de Bayes pour déterminer la probabilité qu’une personne ait la grippe lorsqu’elle a un mal de tête.

Le théorème de Bayes a de nombreuses applications, par exemple, il est utilisé en médecine, en économie ou en technologie pour calculer les probabilités de certains événements conditionnés par d’autres événements. Ci-dessous, nous entrerons dans le détail des différentes applications du théorème de Bayes.

Le théorème de Bayes a été inventé par le mathématicien anglais Thomas Bayes (1702-1761), bien qu’il ait été publié à titre posthume en 1763.

Formule du théorème de Bayes

Le théorème de Bayes dit que étant donné un espace échantillon composé d’un ensemble d’ événements mutuellement exclusifs {A 1 , A 2 ,…, A i ,…, A n } dont les probabilités ne sont pas nulles et un autre événement B, on peut relier mathématiquement les probabilité conditionnelle de A i étant donné l’événement B avec la probabilité conditionnelle de B étant donné A i .

Ainsi, la formule du théorème de Bayes , également connue sous le nom de règle de Bayes , est la suivante :

Formule du théorème de Bayes, règle de Bayes

Où:

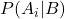  • P(A_i|B) est la probabilité conditionnelle de l’événement A i étant donné l’événement B, appelée probabilité a posteriori.
  • P(B|A_i) est la probabilité conditionnelle de l’événement B étant donné l’événement A i .
  • P(A_i) est la probabilité que l’événement A i se produise, appelée probabilité a priori.

Notez que le dénominateur de la formule du théorème de Bayes correspond à la probabilité totale de l’événement B.

Exemple du théorème de Bayes

Une fois que nous aurons vu la définition du théorème de Bayes et quelle est sa formule, nous allons voir un exemple résolu de la façon dont une probabilité est calculée avec le théorème de Bayes pour mieux comprendre le concept.

  • Un magasin d’électronique vend trois marques de téléviseurs : X, Y, Z. On estime que 20 % des ventes sont des téléviseurs de marque X, 50 % de marque Y et 30 % de marque Z. 5 % des téléviseurs de marque X sont défectueux, 3 % des téléviseurs de marque Y sont défectueux, et 4 % des téléviseurs de marque Z sont défectueux. Étant donné un téléviseur défectueux, quelle est la probabilité qu’il s’agisse d’un téléviseur de marque Z ?

L’exercice nous donne les probabilités qu’un client achète chaque marque de téléviseur :

  • Evénement A 1 : Un client achète un téléviseur de marque X → P(A 1 )=0.20
  • Evénement A 2 : Un client achète un téléviseur de marque Y → P(A 2 )=0.50
  • Evénement A 3 : Un client achète un téléviseur de marque Z → P(A 3 )=0,30

De plus, le relevé nous donne également la probabilité qu’un téléviseur de chaque marque soit défectueux :

Événement B : Le téléviseur est défectueux

  • B|A 1 : Étant donné un téléviseur de marque X, le téléviseur est défectueux → P(B|A 1 )=0.05
  • B|A 2 : Étant donné un téléviseur de marque Y, le téléviseur est défectueux → P(B|A 2 )=0.03
  • B|A 3 : Étant donné un téléviseur de marque Z, le téléviseur est défectueux → P(B|A 3 )=0.04

Ainsi l’ arbre de probabilité de tous les événements qui nous intéressent est le suivant :

Diagramme de l'arbre du théorème de Bayes

Ainsi, pour calculer la probabilité que, étant donné un téléviseur défectueux, ce soit la marque Z, il faut utiliser la formule du théorème de Bayes :

P(A_i|B)=\cfrac{P(B|A_i)\cdot P(A_i)}{\displaystyle \sum_{k=1}^n P(B|A_k)\cdot P(A_k)}

En utilisant la terminologie utilisée dans cet exemple, la formule de Bayes ressemble à ceci :

P(A_3|B)=\cfrac{P(B|A_3)\cdot P(A_3)}{P(B|A_1)\cdot P(A_1)+P(B|A_2)\cdot P(A_2)+ P(B|A_3)\cdot P(A_3)}

Ainsi, le calcul de la probabilité qu’un téléviseur défectueux donné soit de marque Z est le suivant :

\begin{aligned}P(A_3|B)&=\cfrac{P(B|A_3)\cdot P(A_3)}{P(B|A_1)\cdot P(A_1)+P(B|A_2)\cdot P(A_2)+ P(B|A_3)\cdot P(A_3)}\\[2ex]&=\cfrac{0,04\cdot 0,30}{0,05\cdot 0,20+0,03\cdot 0,50+0,04\cdot 0,30}\\[2ex]&=0,32\end{aligned}

En conclusion, la probabilité que si un téléviseur est défectueux, ce soit la marque Z est de 32 %.

Applications du théorème de Bayes

Les applications du théorème de Bayes sont nombreuses, parmi lesquelles :

  1. Tests médicaux : Le théorème de Bayes est fréquemment utilisé en médecine pour déterminer la probabilité de réussite des tests diagnostiques. Par exemple, dans le cas d’un test VIH, le théorème peut être utilisé pour calculer la probabilité qu’une personne soit réellement porteuse du virus si le résultat du test est positif.
  2. Analyse financière : En finance, le théorème de Bayes est utilisé pour calculer la probabilité que certains événements économiques, comme une augmentation ou une diminution de la valeur des actions, se produisent compte tenu d’un ensemble de variables économiques.
  3. Etude de marché : Le théorème de Bayes permet de déterminer, par exemple, la probabilité qu’une personne achète un produit après avoir vu une publicité pour ce produit.
  4. Prévisions météorologiques : les modèles météorologiques utilisent également le théorème de Bayes pour déterminer la probabilité qu’une prévision météorologique donnée basée sur les données observées se réalise. Cela améliore la précision des prévisions climatiques.
  5. Sécurité informatique – En cybersécurité, le théorème de Bayes peut être appliqué pour déterminer la probabilité qu’une activité suspecte soit véritablement une attaque contre le système informatique.

Problèmes résolus du théorème de Bayes

Exercice 1

On estime que 1 % de la population souffre d’une certaine maladie. Un test pour détecter cette maladie est précis à 95 % pour les cas positifs et à 90 % pour les cas négatifs. Si une personne sélectionnée au hasard est testée positive, quelle est la probabilité qu’elle soit réellement atteinte de la maladie ?

L’énoncé de l’exercice nous donne les probabilités suivantes :

A 1 : La personne a la maladie → P(A 1 )=0,01
A 2 : La personne n’a pas la maladie → P(A 2 )=0,99

B : Le test est positif
B|A 1 : Le test est positif lorsque la personne est atteinte de la maladie → P(B|A 1 )=0,95
B|A 2 : Le test est positif lorsque la personne n’a pas la maladie → P(B|A 2 )=1-0.90=0.10

Ensuite, pour calculer la probabilité qu’une personne sélectionnée au hasard soit réellement atteinte de la maladie lorsqu’elle est testée positive, la règle de Bayes doit être appliquée :

P(A_i|B)=\cfrac{P(B|A_i)\cdot P(A_i)}{\displaystyle \sum_{k=1}^n P(B|A_k)\cdot P(A_k)}

P(A_1|B)=\cfrac{P(B|A_1)\cdot P(A_1)}{P(B|A_1)\cdot P(A_1)+P(B|A_2)\cdot P(A_2)}

Nous substituons donc les valeurs dans la formule et effectuons le calcul de probabilité :

\begin{aligned}P(A_1|B)&=\cfrac{P(B|A_1)\cdot P(A_1)}{P(B|A_1)\cdot P(A_1)+P(B|A_2)\cdot P(A_2)}\\[2ex]&=\cfrac{0,95\cdot 0,01}{0,95\cdot 0,01+0,10\cdot 0,99}\\[2ex]&=0,0876\end{aligned}

En bref, la probabilité qu’une personne choisie au hasard soit positive et soit réellement atteinte de la maladie est de 8,76 %.

Exercice 2

On estime que la probabilité qu’un titre augmente en une journée est de 40 %, qu’il reste stable est de 10 % et qu’il baisse est de 50 %. De plus, on sait que lorsque le marché augmente, il y a une probabilité de 90 % qu’un analyste financier le prédise correctement, que lorsque le marché reste stable, la probabilité que la prédiction soit correcte est de 75 % et qu’en cas de baisse, la probabilité d’une prédiction correcte est de 75 %. 85%.%. Si un analyste prédit que le marché va baisser, quelle est la probabilité qu’il baisse réellement ?

Dans ce cas, l’énoncé de l’exercice nous fournit les probabilités suivantes :

A 1 : Le marché monte en un jour → P(A 1 )=0,40
A 2 : Le marché reste stable sur une journée → P(A 2 )=0,10
A 3 : Le marché monte en un jour → P(A 3 )=0,50

B : L’analyste prédit que le marché va baisser
B|A 1 : L’analyste prédit correctement que le marché va augmenter → P(B|A 1 )=0.90
B|A 2 : L’analyste prédit correctement que le marché reste stable → P(B|A 2 )=0,75
B|A 3 : L’analyste prédit correctement que le marché va baisser → P(B|A 3 )=0.85

Pour déterminer la probabilité qu’un analyste fasse une prédiction selon laquelle le marché baissera et qu’elle soit correcte, nous devons utiliser la formule du théorème de Bayes :

P(A_i|B)=\cfrac{P(B|A_i)\cdot P(A_i)}{\displaystyle \sum_{k=1}^n P(B|A_k)\cdot P(A_k)}

P(A_3|B)=\cfrac{P(B|A_3)\cdot P(A_3)}{P(B|A_1)\cdot P(A_1)+P(B|A_2)\cdot P(A_2)+ P(B|A_3)\cdot P(A_3)}

Nous substituons les valeurs de probabilité dans la formule de Bayes et calculons la probabilité :

\begin{aligned}P(A_3|B)&=\cfrac{P(B|A_3)\cdot P(A_3)}{P(B|A_1)\cdot P(A_1)+P(B|A_2)\cdot P(A_2)+ P(B|A_3)\cdot P(A_3)}\\[2ex]&=\cfrac{0,85\cdot 0,50}{0,90\cdot 0,40+0,75\cdot 0,10+0,85\cdot 0,50}\\[2ex]&=0,4942\end{aligned}

Par conséquent, la probabilité qu’un analyste ait raison lorsqu’il dit que le marché boursier va baisser est de 49,42 %.

à propos de l'auteur

Amelia Rodriguez
Pr Amélia Rodriguez

En mettant l'accent sur l'apprentissage interactif et les applications pratiques, la professeure Amélia Rodriguez propose des tutoriels complets et des exemples concrets pour rendre les concepts de probabilité accessibles et pertinents pour la vie de ses étudiants. Lire plus

Ajouter un commentaire

Votre adresse e-mail ne sera pas publiée. Les champs obligatoires sont indiqués avec *