Comment appliquer le théorème central limite dans R (avec exemples)

Le théorème central limite stipule que la distribution d’échantillonnage d’une moyenne d’échantillon est approximativement normale si la taille de l’échantillon est suffisamment grande, même si la distribution de la population n’est pas normale.

Le théorème central limite indique également que la distribution d’échantillonnage aura les propriétés suivantes :

1. La moyenne de la distribution d’échantillonnage sera égale à la moyenne de la distribution de la population :

x = µ

2. L’écart type de la distribution d’échantillonnage sera égal à l’écart type de la distribution de la population divisé par la taille de l’échantillon :

s = σ / n

L’exemple suivant montre comment appliquer le théorème central limite dans R.

Exemple : application du théorème central limite dans R

Supposons que la largeur de la carapace d’une tortue suive une distribution uniforme avec une largeur minimale de 2 pouces et une largeur maximale de 6 pouces.

Autrement dit, si nous sélectionnons une tortue au hasard et mesurons la largeur de sa carapace, il est également probable qu’elle ait une largeur comprise entre 2 et 6 pouces.

Le code suivant montre comment créer un ensemble de données dans R contenant les mesures des largeurs de carapace de 1 000 tortues, uniformément réparties entre 2 et 6 pouces :

#make this example reproducible
set.seed(0)

#create random variable with sample size of 1000 that is uniformally distributed
data <- runif(n=1000, min=2, max=6)

#create histogram to visualize distribution of turtle shell widths
hist(data, col='steelblue', main='Histogram of Turtle Shell Widths')

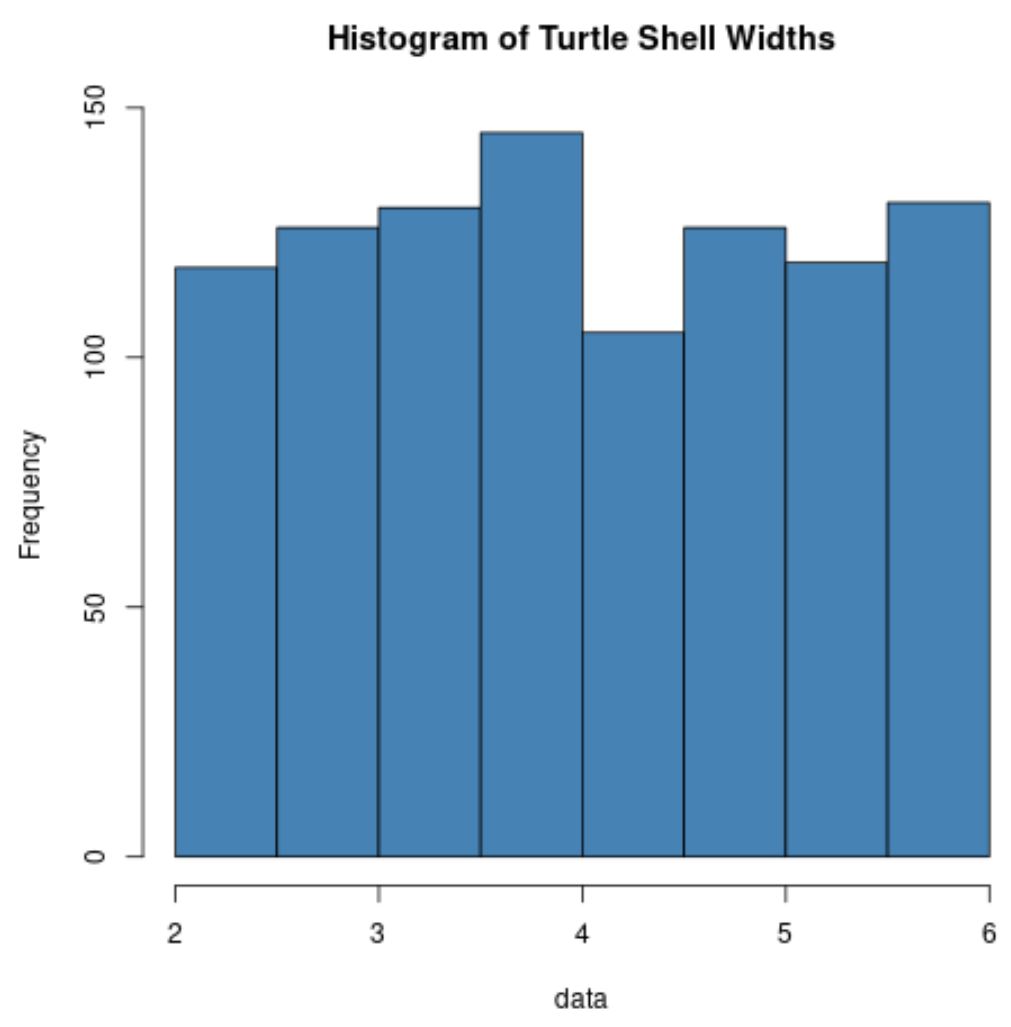
Notez que la distribution des largeurs de carapace de tortue n’est normalement pas du tout distribuée.

Imaginez maintenant que nous prenions des échantillons aléatoires répétés de 5 tortues de cette population et que nous mesurions la moyenne de l’échantillon encore et encore.

Le code suivant montre comment effectuer ce processus dans R et créer un histogramme pour visualiser la distribution des moyennes des échantillons :

#create empty vector to hold sample means
sample5 <- c()

#take 1,000 random samples of size n=5
n = 1000
for (i in 1:n){
sample5[i] = mean(sample(data, 5, replace=TRUE))
}

#calculate mean and standard deviation of sample means
mean(sample5)

[1] 4.008103

sd(sample5)

[1] 0.5171083 

#create histogram to visualize sampling distribution of sample means
hist(sample5, col ='steelblue', xlab='Turtle Shell Width', main='Sample size = 5')

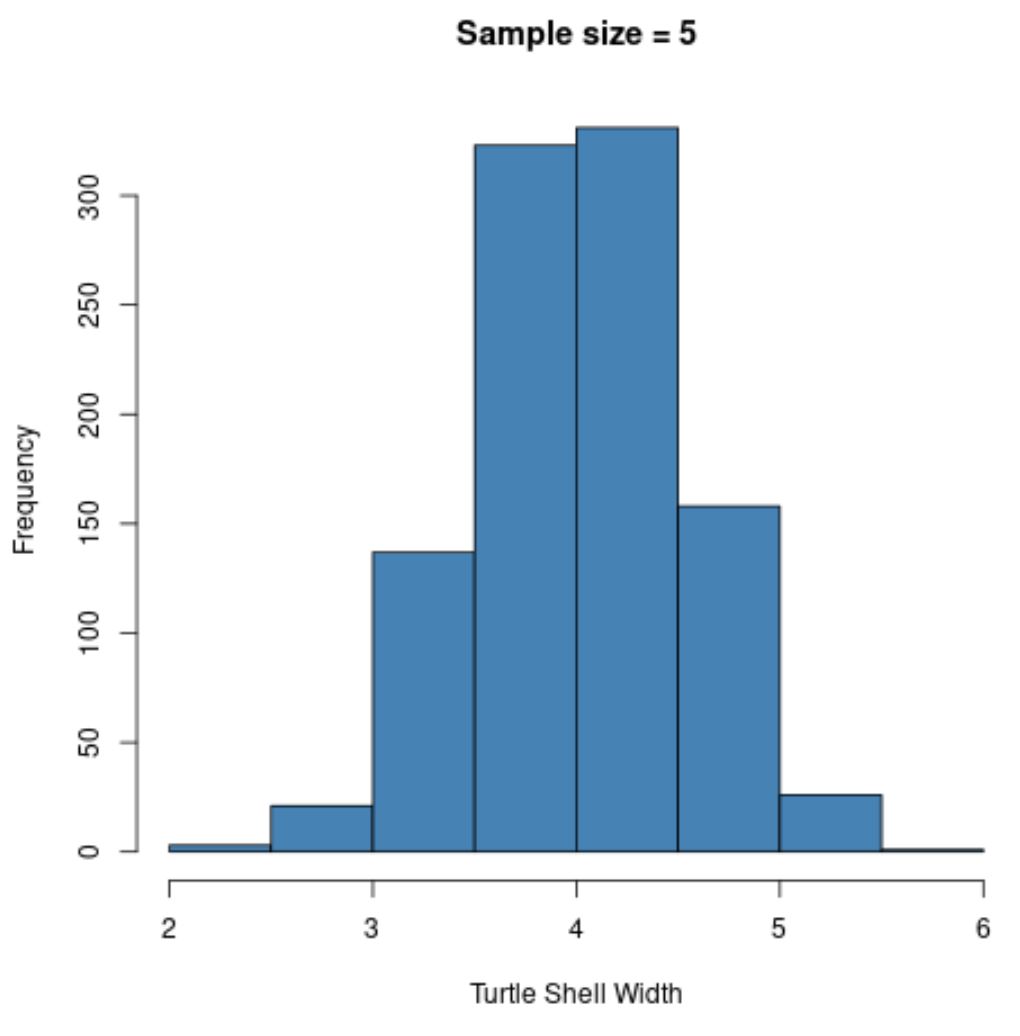
Notez que la distribution d’échantillonnage des moyennes de l’échantillon apparaît normalement distribuée, même si la distribution d’où proviennent les échantillons n’était pas normalement distribuée.

Notez également la moyenne de l’échantillon et l’écart type de l’échantillon pour cette distribution d’échantillonnage :

• x̄ : 4.008
• s : 0,517

Supposons maintenant que nous augmentions la taille de l’échantillon que nous utilisons de n=5 à n=30 et que nous recréions l’histogramme des moyennes de l’échantillon :

#create empty vector to hold sample means
sample30 <- c()

#take 1,000 random samples of size n=30
n = 1000
for (i in 1:n){
sample30[i] = mean(sample(data, 30, replace=TRUE))
}

#calculate mean and standard deviation of sample means
mean(sample30)

[1] 4.000472

sd(sample30)

[1] 0.2003791

#create histogram to visualize sampling distribution of sample means
hist(sample30, col ='steelblue', xlab='Turtle Shell Width', main='Sample size = 30')

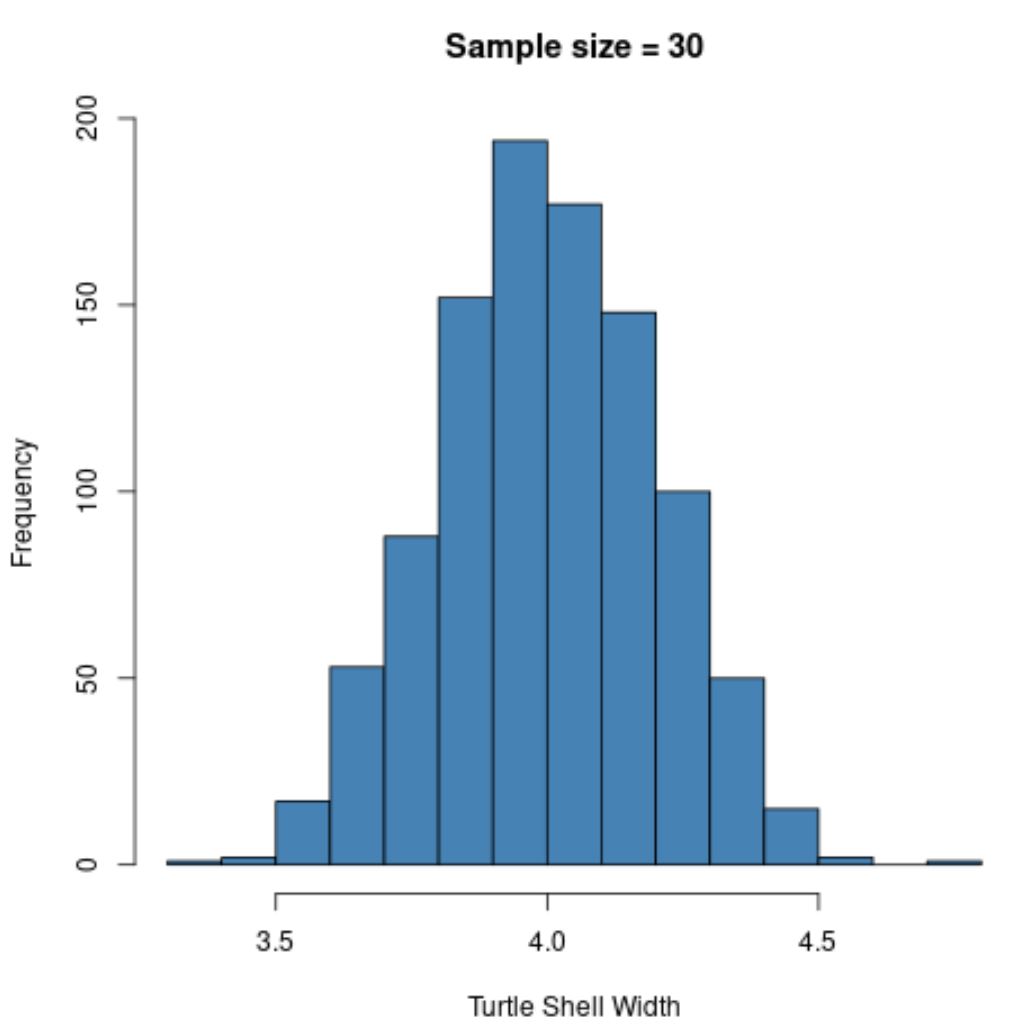
La distribution d’échantillonnage est à nouveau normalement distribuée , mais l’écart type de l’échantillon est encore plus petit :

• s : 0,200

En effet, nous avons utilisé une taille d’échantillon plus grande (n = 30) par rapport à l’exemple précédent (n = 5), de sorte que l’écart type des moyennes de l’échantillon est encore plus petit.

Si nous continuons à utiliser des échantillons de plus en plus grands, nous constaterons que l’écart type de l’échantillon devient de plus en plus petit.

Ceci illustre le théorème central limite dans la pratique.

Ressources additionnelles

Les ressources suivantes fournissent des informations supplémentaires sur le théorème central limite :

Une introduction au théorème central limite
Calculateur du théorème central limite
5 exemples d’utilisation du théorème central limite dans la vie réelle